图

Posted 2022-08-12 huatian5

图

 

一.图的基本概念

1.无向图与有向图

此处要熟悉一下无序对与无序积的概念；

集合中有元素重复出现的话就称为多重集合，简称多重集，元素在多重集合中出现的次数称为该元素的重复度；

无向图：只有无向边的图

标定图：顶点标定了名字

非标定图：顶点未标定名字

有向图：只有有向边的图

n阶图：有n个顶点的图

零图：没有边

平凡图：一阶零图（只有一个顶点，没有边）

空图：顶点集为空

2.顶点的度数和握手定理

度数：关联边的条数，有向图的顶点度数又分为入度和出度

悬挂顶点：度数为1的顶点

悬挂边：与悬挂顶点相关联的边

握手定理：顶点的度数和 = 2*边数

推论：任何图，度数为奇数的顶点个数是偶数

3.简单图、完全图、正则图、圈图、轮图、方体图

平行边：无向图中，关联一对顶点的无向边多余一条（有向图中的平行边必须方向相同）

重数：平行边的条数

多重图：含平行边的图

简单图：不含平行边和环的图

完全图：图中任意一个顶点都与其余的n-1个顶点相邻

正则图：每个顶点的度数都是相等的，例如正多边形

圈图：边首尾相连

轮图：圈图里面放一个顶点，这个顶点与其他所以顶点相邻，例如：车轮

方体图：2^n阶无向简单图，顶点用0和1的组合来标记，相邻顶点仅有一位数字不同

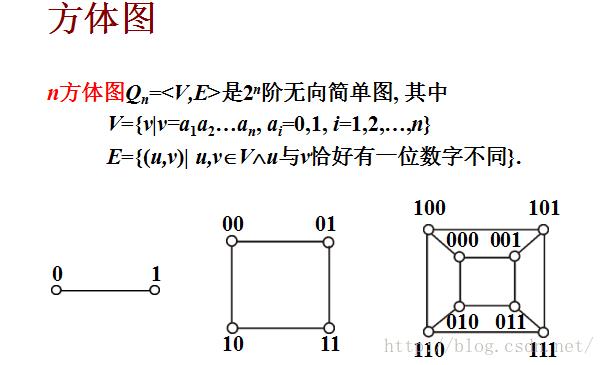
4.子图、补图

子图：顶点和边都是母图里面的

导出子图：顶点为母图中所有顶点的子图

导出子图：顶点导出子图、边导出子图

5.图的同构

根据图的同构定义，可以给出图同构的必要条件：
(1) 结点数目相等；
(2) 边数相等；
(3) 度数相同的结点数目相等。
但这仅仅是必要条件而不是充分条件。

 

二.图的连通性

1.通路与回路

2.无向图的连通性与连通度

 

三.图的矩阵表示

1.无向图的关联矩阵

点与边

2.有向无环图的关联矩阵

3.有向图的邻接矩阵

点与点

4.有向图的可达矩阵

只有0和1

 

四.几种特殊的图

1.二部图

（又被称为偶图、双图、二分图）

是二部图的充要条件：图中无奇数长度的回路

需注意：最大匹配、完备匹配、完美匹配。

Hall定理

t条件

2.欧拉图

欧拉通路的定义

欧拉回路的定义

欧拉图：具有欧拉回路的图

条件：是连通图且无奇度顶点

格尼斯堡问题无解

3.哈密顿图

哈密顿通路

哈密顿回路

哈密顿图：是具有哈密顿回路的图

判定定理：1.根据连通分支的个数    2.有割点的图一定不是哈密顿图    3.d(u)+d(v)>=n则是哈密顿图

补个今天考试遇到的问题：某次会议有20人参加，某中每人都至少有10个朋友，这20人围一圆桌入席，要想使每个人相邻的两位都是朋友是否可能?根据是什么?

答案：证明  可用结点代表人，根据题意，两人是朋友时相应结点间连一条边，则得到一个无向图G=(V，E)，可转化为求哈密顿回路问题．由于对任意结点u，v∈V，有d(u)10，d(v)10，因而d(u)+d(v)>=20．
根据求哈密顿回路的充分条件定理，可知G中存在哈密顿回路，G为哈密顿图．

利用的定理：d(u)+d(v)>=n则是哈密顿图

4.平面图

边界定义

次数：边界的长度

定理：所有面的次数之和为边数的二倍

极大平面图的定义

平面图这块不是一般的重要
需要掌握的有
欧拉公式
n-m+r=p(G)+1
连通图的时候
n-m+r=2
库拉图斯基定理：
不含与K5和K3，3同胚的子图
对偶图：
n*=r   顶点==面数
m*=m   边数==边数
r*=n   面数==顶点数

待补充……