音频基础学习二——声音的波形
Posted 山河君
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了音频基础学习二——声音的波形相关的知识,希望对你有一定的参考价值。
文章目录
前言
上一章记录了声音是如何产生的,以及声音的一些基本的特性和术语,我们知道声音是由物体振动而产生的一种波。例如以下是小提琴、小号、长笛、双簧管的波形:
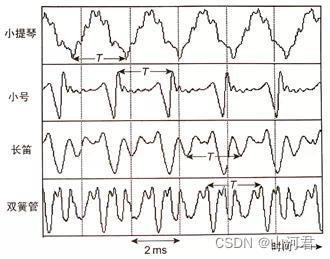
那么为什么他们的波形是长这样呢?本章内容会深入解析声音的波形是由何而来,而在进入内容之前,以下这段话会在本文中出现多次:
重要的事情说三遍:
傅立叶原理表明:任何重复的波形都可以分解为含有基波频率和一系列为基波倍数的谐波的正弦波分量。
傅立叶原理表明:任何重复的波形都可以分解为含有基波频率和一系列为基波倍数的谐波的正弦波分量。
傅立叶原理表明:任何重复的波形都可以分解为含有基波频率和一系列为基波倍数的谐波的正弦波分量。
先以一张图来解释上面这句话的意思,以下是几段波的合成,就成了我们经常看到的波:
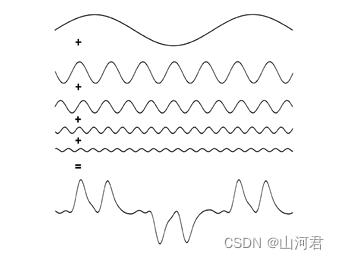
其实如果只是想了解一下,那么看完前言其实就可以了;如果对于正弦波是什么有一定了解的那么建议直接看第三段,当如如果一点也不了解的,笔者在这里会很详细的进行介绍。
|版本声明:山河君,未经博主允许,禁止转载
一、声音的基础波形
声音的基础波形典型的有以下几种:
1.正弦波
正弦波(Sine Wave)是频率成分最单一的一种波形。这种波形是数学上的正弦曲线。它听起来清楚明了,只包括第一和声,是一种基础音调
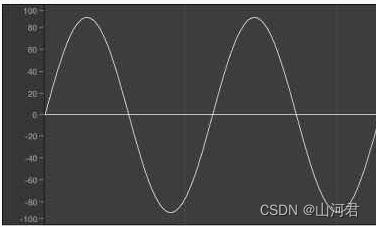
2.三角波
三角波的形状和横轴一起构成了两个三角形,常被认为是正弦波,因为滚降速度过快,所以听起来更加柔和
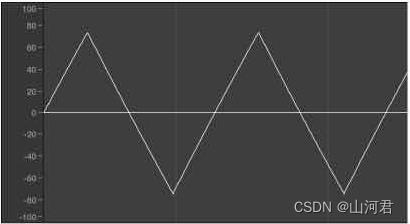
3.锯齿波
锯齿波的波形形状与三角波较为相似,但是锯齿波的波形中存在着突变的点。所以听起来更加的清晰明亮。
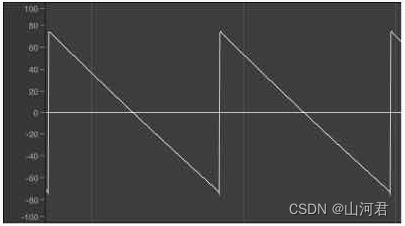
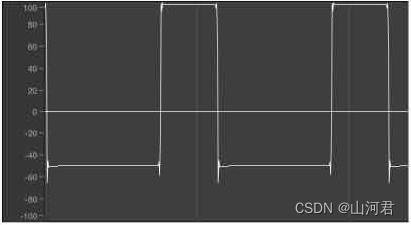
4.方波
方波是一种非正弦曲线的波形,理想情况下的方波只有“高”和“低”两个值。所以听起来比较空旷。
二、正弦波
为什么把正弦波单独拎出来,是因为它是比较重要的一种波形:
傅立叶原理表明:任何重复的波形都可以分解为含有基波频率和一系列为基波倍数的谐波的正弦波分量。
1.什么是正弦
复习一下初中数学:正弦函数是三角函数的一种,三角函数分为正弦、余弦、和正切。在直角三角形中,任意一锐角∠A的对边与斜边的比叫做∠A的正弦。
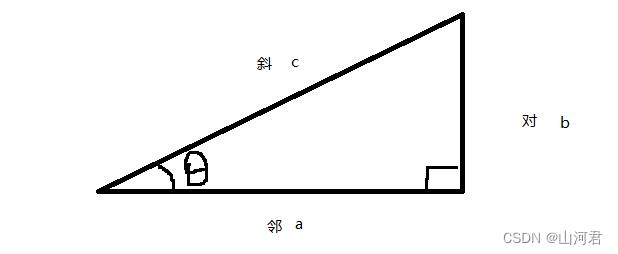
θ是要求的角度,角度的对面的边是对边,而三角形最长的边是斜边,另一个边是邻边。
三角函数sin cos tan的定义是:
-
sinθ=对边/斜边 = b / c
-
cosθ=邻边/斜边 = a / c
-
tanθ=对边/邻边 = b / a
2.什么是正弦波和正弦曲线
百度百科上解释:
正弦波是频率成分最为单一的一种信号,因这种信号的波形是数学上的正弦曲线而得名。
现假设一个函数为 y=sin X,当 X 分别取 0、30、60、90、120、150、180 时(单位:度),Y对应的数值分别为 0、0.5、0.8660、1、0.8660、0.5、0。在坐标系中画出对应的点就可以得出正弦波的图像了。该图像有一个特点,就是周期性变化,例如 X = 0 时,Y = 0,X = 180 时, Y = 0;若 X 取值【180~360】,则我们可以看到,图像正好与原来的相反(在第四象限)。这就是正弦波的图像了。
直观的感受一下正弦曲线是什么样子的:
x为0角度:

当x为30度时:
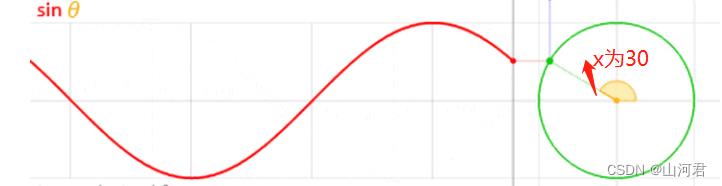
当x为60度时
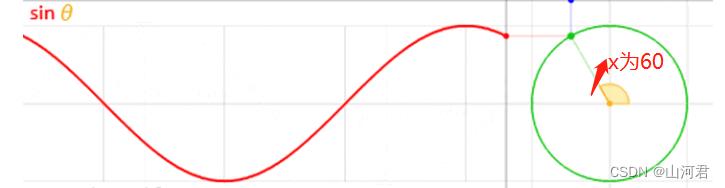
当x为90度时:
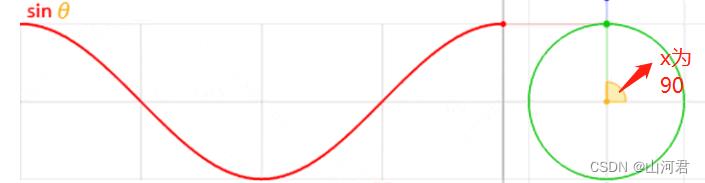
整体看起来如下
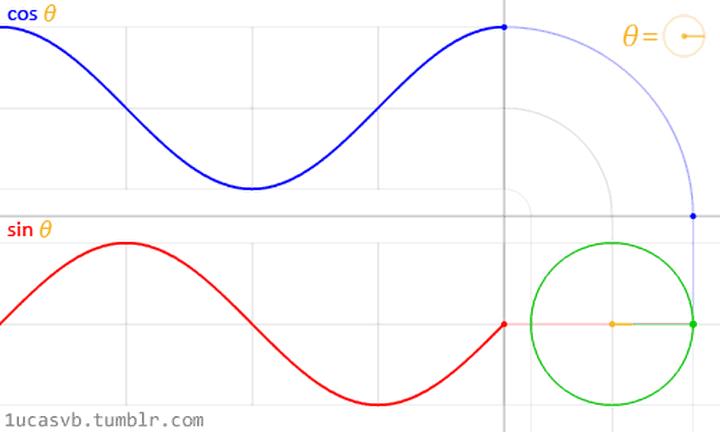
-----------图片来自知乎遇见数学-----------
我们可以很直观的看到,曲线y轴的坐标,和圆心的角度、速度、半径有着某种直接的联系。
三、正弦波与声音
傅立叶原理表明:任何重复的波形都可以分解为含有基波频率和一系列为基波倍数的谐波的正弦波分量。
1.角频率
角频率表示单位时间内变化的相角弧度值
再深入了解第二段第二节正弦曲线的
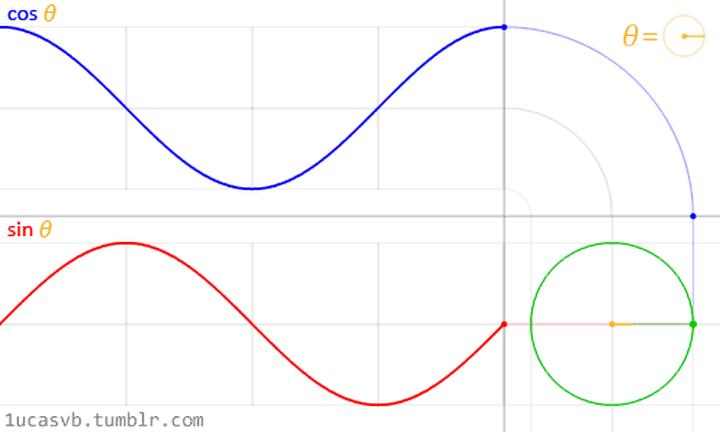
如果像图片里一样:已知圆的半径是x,频率为f,那么在t时,y的值为
那么有公式:y = x * sin(f * t * 360°)
又知道转一圈也就是一个周期(f * t = 1),f = 1 / t; 又知道转一圈,角弧度转了2π, 所以角频率:w = 2π / t = 2πf
又由于每一个周期都是360°,也同样是2π, 所以又有公式:y = x * sin(2πft)
2.基波和谐波
基波:
又叫基频,复合波(多个波的合成)的最低频率分量,也就是说周期最大(频率最小)且幅度最大的那个就是基波。基波决定了声音的音调。
谐波:
是指对周期性非正弦交流量进行傅里叶级数分解所得到的大于基波频率整数倍的各次分量,其频率比信号的主要频率高。
例如基波基频为50Mhz,则谐波出现在100Mhz,200Mhz…(基频的整数倍),音频中,谐波的作用就是美化声音赋予色彩。
图解
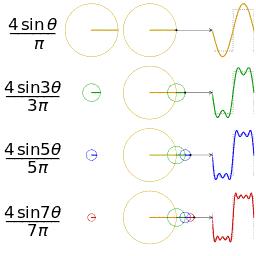
下面这张图片分别是基波、二次谐波、三次谐波的图片
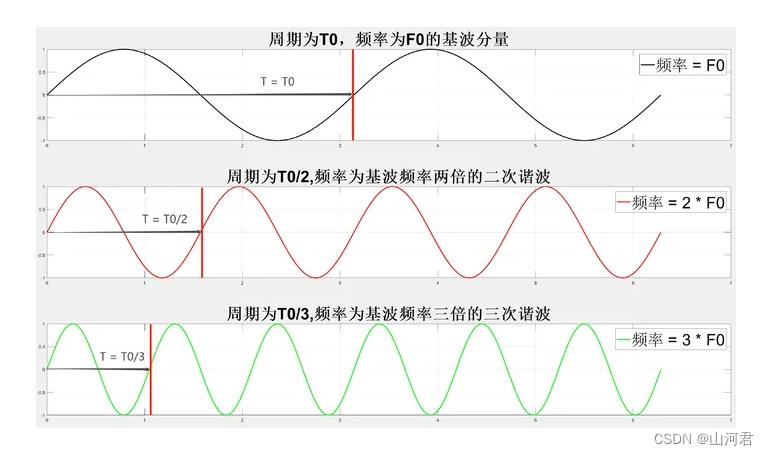
3.波形的合成
上面已经得出来一个公式:y = x * sin(2πft),而波的合成就是当t相同时,y的相加
下图是半径为1,频率为100和频率为200的波进行相加后的结果:
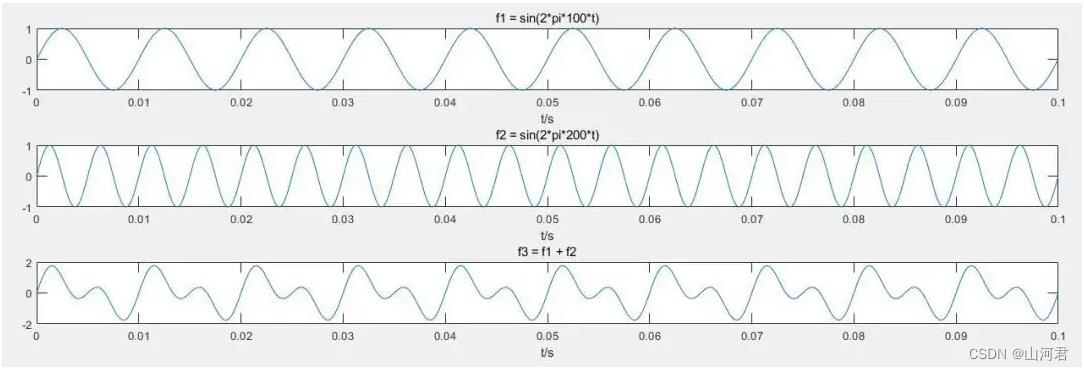
三角波的形成:
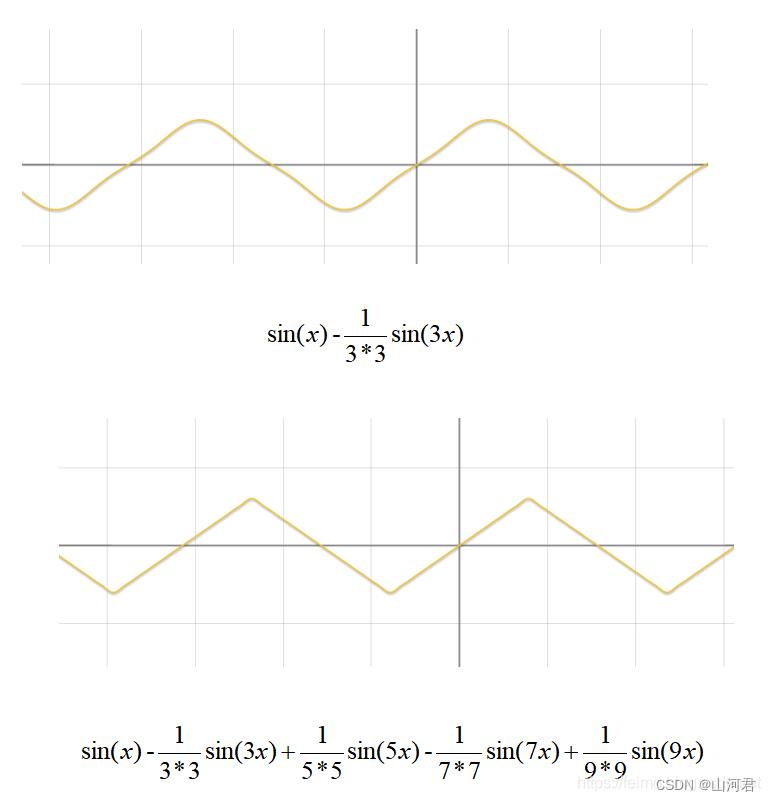
-----------图片来自Dezeming博客-----------
方波的形成:
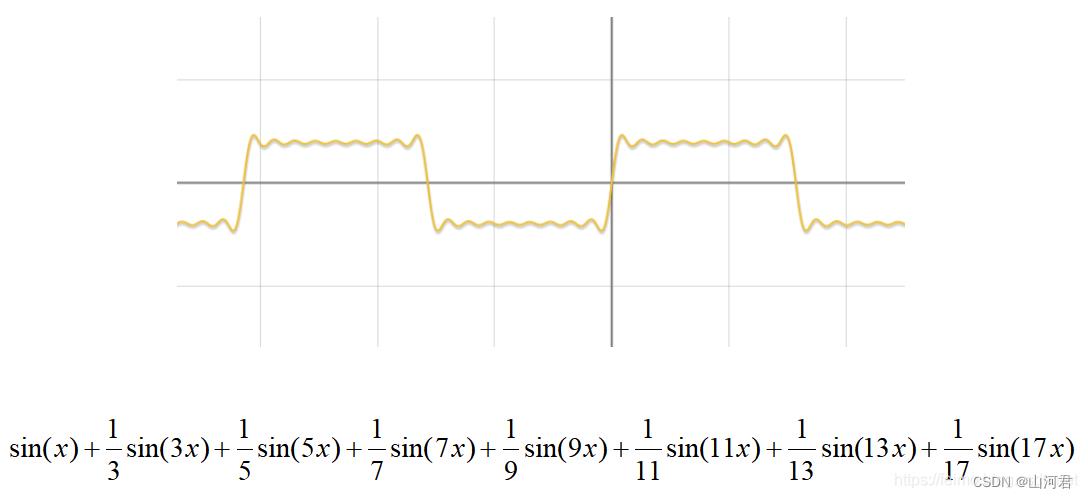
-----------图片来自Dezeming博客-----------
当子项无穷多以后,叠加出来的效果就是方波:
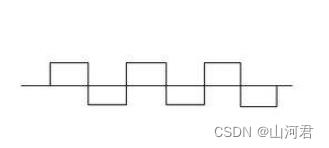
波形相加实际就是如下图画出:
总结
以上是对声音的波形是如何形成的做了详细的介绍,其中涉及到大量的数学知识,看起来还是比较绕脑,但个人觉得还是比较有趣的。
如果对您有所帮助,请帮忙点个赞吧!
音频基础学习三——声音的时频谱
文章目录
前言
在上一篇文章中,我们了解到:任何重复的波形都可以分解为含有基波频率和一系列为基波倍数的谐波的正弦波分量,同时记录了一些基本的波形。
本章内容是对音频测量进行简述,一般来说,我们讨论音频测量的概念基本都是对于声音信号的时域和频域有关。任何声音都可以通过这两种形式来进行表现。
时域与频域
1.什么是时域?
描述信号与时间的关系,一个信号的时域波形可以表述为信号随时间变化的曲线。其自变量是时间,即横轴是时间,纵轴是信号的变化。
2.什么是频域?
指信号随频率变化的曲线。自变量是频率,即横轴是频率,纵轴是该频率信号的幅度,也就是通常说的频谱图。
3.一张图理解时域和频域
时域是真实存在的,记录的是不同时间时,信号的一个幅度变化。而频域是虚构的,是我们根据傅里叶变换,将一段声音分为了基波和谐波。
由下图我们很直观的看到,时域的波形被分解为若干个不同频率,不同幅值的正弦波,根据频率和幅值,我们就画出了在某一段时间内,频域的图像。

4.意义
我们干嘛要费那么大力气来画时域和频域的图像?通过图像我们能分析出来什么?
在之前的文章声音的本质中我们讲过声音的三大特性:
- 响度:其他条件不变,振幅越大,人听着越响。
- 音调:其他条件不变,频率越高,音调越高,类似于男低音,女高音。
- 音色:其他条件不变,谐波会影响音色,例如我们可以很容易听出来笛子和口琴的区别。
看到这里还会有一些迷糊吗?没关系,举几个特别通俗的例子:
例子1:
现在听到的声音过小,想把声音调大怎么做?
在时域图像上,将幅值调大,那么响度就会变大。
例子2:
现在有超声波,有人声,有低声波,但是超声波和低声波我都听不到,只能听到人声,那么我不想记录下超声和低声的声波怎么做?
我们之前有说过,人耳听到的频率在20 Hz~20000 Hz之间,所以根据频域,我们可以将低于20Hz,高于20000Hz的波给剔除出去,那么就只有人声在了
例子三:
现在有人声,又有敲桌子声,我只想听人声,怎么办?
因为人声和敲击桌子声都是在20Hz~20000Hz之间,我们可以通过把桌子的谐波记录下来,对比此时的谐波,剔除桌子的谐波,那么就只有人声在了(虽然可能会影响人声)
总结
时域图和频域图是我们对于声音进行解析和优化的基础,本章对于时域和频域做了简单的介绍,接下来的文章会进行详细的对于若何获得频域图进行介绍。
如果对您有所帮助,请帮忙点个赞吧!
以上是关于音频基础学习二——声音的波形的主要内容,如果未能解决你的问题,请参考以下文章