蓝桥杯AcWing 题目题解 - 二分与前缀和差分
Posted 小黄同学LL
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了蓝桥杯AcWing 题目题解 - 二分与前缀和差分相关的知识，希望对你有一定的参考价值。
目录
整数二分步骤:
1.找一个区间[L，R]，使得答案一定在该区间中
2找一个判断条件，使得该判断条件具有二段性，并且答案一定是该二段性的分界点。
3.分析终点M在该判断条件下是否成立，如果成立，考虑答案在哪个区间;如果不成立，考虑答案在哪个区间;
4.如果更新方式写的是R（右） = Mid，则不用做任何处理;如果更新方式写的是L（左）= Mid，则需要在计算Mid时加上1。
AcWing 789. 数的范围 - 整数二分
给定一个按照升序排列的长度为n的整数数组，以及q个查询。
对于每个查询，返回一个元素k的起始位置和终止位置(位置从О开始计数)。如果数组中不存在该元素，则返回-1 -1 。
输入格式
第一行包含整数n和q，表示数组长度和询问个数。
第二行包含n个整数（均在1～10000范围内)，表示完整数组。接下来q行，每行包含一个整数k，表示一个询问元素。
输出格式
共q行，每行包含两个整数，表示所求元素的起始位置和终止位置。如果数组中不存在该元素，则返回-1 -1。
数据范围
1<n ≤100000
1≤q≤10000
1≤k ≤10000
输入样例:
6 3
1 2 2 3 3 4
3
4
5
输出样例：
3 4
5 5
-1 -1#include<iostream>
using namespace std;
const int N=100010;
int n,m;
int q[N];
int main()
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++) scanf("%d",&q[i]);
while(m--)
int x;
scanf("%d",&x);
int l=0,r=n-1;
while(l<r) //取始下标
int mid=l+r>>1;
if(q[mid]>=x) r=mid;
else l=mid+1;
if(q[l]!=x) cout<<"-1 -1"<<endl;
else
cout<<l<<' ';
int l=0,r=n-1;
while(l<r) //取末下标
int mid=l+r+1>>1;
if(q[mid]<=x) l=mid;
else r=mid-1;
cout<<l<<endl;
return 0;
记忆：写完模板后看案例分析始末下标，当 l （左）= mid 时必须mid+1
AcWing 790. 数的三次方根 - 实数二分
给定一个浮点数n，求它的三次方根。
输入格式
共一行，包含一个浮点数n。
输出格式
共一行，包含一个浮点数，表示问题的解。注意，结果保留6位小数。
数据范围
-10000<n≤10000
输入样例：
1000.00
输出样例：
10.000000#include<iostream>
using namespace std;
int main()
double l=-100000,r=100000; //数据结果必在其之间，不用思考
double n,m;
cin>>n;
while(r-l>1e-8) //精确到为1e-6，所以至少要多精确两位
m=(l+r)/2;
if(m*m*m>=n) r=m; //立方根n在mid的左边，缩右边界
else l=m;
printf("%.6f",m);
return 0;
AcWing 730. 机器人跳跃问题 - 二分应用
来源：今日头条2019，笔试题
输入样例1：
5
3 4 3 2 4
输出样例1：
4
输入样例2：
3
4 4 4
输出样例2：
4
输入样例3：
3
1 6 4
输出样例3：
3思路：
如例一高度 3 4 3 2 4
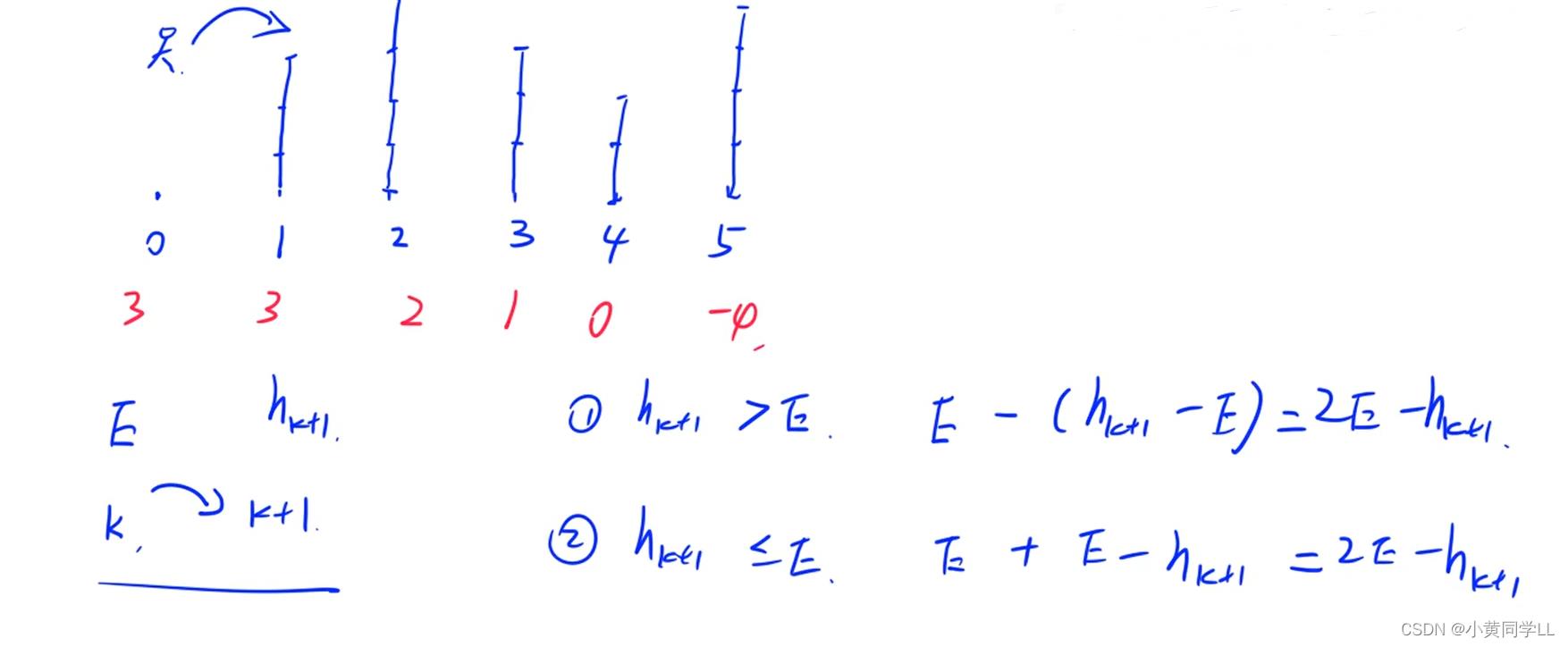
可以发现通过计算 E=2E-H(k+1)，那么只需要将数组所有值带入公式，找到刚好大于0的E即可；
- 利用二分，check函数为 将数组所有值带入公式
- 如果e<0则不满足要求，返回fasle；
- 如果e大于数组中最大值，由公式E=2E-H(k+1)得，E将永远大于0，可直接返回true（此操作可以防止2E太大爆int，同时可以节省时间）
#include<iostream>
#include<cstring>
using namespace std;
const int N=1e5+10;
int n;
int h[N];
bool check(int e)
for(int i=1;i<=n;i++)
e=e*2-h[i];
if(e<0) return false;
if(e>1e5) return true;//防止爆int
return true;
int main()
cin>>n;
for(int i=1;i<=n;i++) cin>>h[i];
int l=0,r=1e5;
while(l<r)
int mid=l+r>>1;
if(check(mid)) r=mid;
else l=mid+1;
cout<<l<<endl;
return 0;
总结：
当题目求“至少”、“至多”，且具有二段性or单调性时，可以考虑二分
（二段性：以某个值为临界，这个值一边的都满足要求，另一边都不满足）
AcWing 1227. 分巧克力
来源：第八届蓝桥杯省赛C++A/B组,第八届蓝桥杯省赛JAVAA/B组
输入样例：
2 10
6 5
5 6
输出样例：
2 
具有单调性与二段性，用二分！
#include<iostream>
using namespace std;
int n,k;
const int N=1e5+10;
int h[N],w[N];
int check(int m)
int ret=0;
for(int i=0;i<n;i++)
ret+=(h[i]/m)*(w[i]/m);
if(ret>=k) return 1;
return 0;
int main()
cin>>n>>k;
for(int i=0;i<n;i++) cin>>h[i]>>w[i];
int l=1,r=1e5;
while(l<r)
int mid=l+r+1>>1;
if(check(mid)) l=mid;
else r=mid-1;
cout<<l;
return 0;
AcWing 795. 前缀和
输入一个长度为n的整数序列。
接下来再输入m个询问，每个询问输入一对l, r。
对于每个询问，输出原序列中从第 l 个数到第r个数的和。
输入格式
第一行包含两个整数n和m。
第二行包含n个整数，表示整数数列。
接下来m行，每行包含两个整数l和r，表示一个询问的区间范围。
输出格式
共m行，每行输出一个询问的结果。
数据范围
1≤l<r ≤n，1 ≤n, m ≤100000,
—1000≤数列中元素的值≤1000
输入样例：
5 3
2 1 3 6 4
1 2
1 3
2 4
输出样例：
3
6
10#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1e5+10;
int n,m;
int a[N];
int s[N];
int main()
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>a[i];
s[i]=s[i-1]+a[i];
while(m--)
int l,r;
cin>>l>>r;
cout<<s[r]-s[l-1]<<endl;
return 0;
k倍区间
来源：第八届蓝桥杯省赛C++B组,第八届蓝桥杯省赛JAVAB组
思路：
- 区间[l,r]的和是k的倍数即(sum[r] - sum[l-1])%k == 0 即sum[r]%k == sum[l-1]%k ；
- 简单来讲，sum[r] % k 和 sum[l-1] % k 的余数如果相等，那么sum[r] - sum[l-1]的差值必然是k的倍数 ，比如说：13 % 7 == 20 % 7 等价于(20-13)%7 =0；
- ans一开始是表示的相减满足题目的条件，因为一旦再出现%k和res数组里面有相当的情况，就全加一遍（和前面全部组合一遍），然后res【sum【i】】++
- cnt[0]=1解释：不置为1的话，那么就少了自身单独一个就可以成立的情况
#include<iostream>
using namespace std;
typedef long long ll;
const int N=1e5+10;
int n,k;
ll s[N];
int cnt[N];
int main()
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)
scanf("%lld",&s[i]);
s[i]+=s[i-1];
ll ans=0;
cnt[0]=1;
for(int i=1;i<=n;i++)
ans+=cnt[s[i]%k];
cnt[s[i]%k]++;
cout<<ans;
return 0;
AcWing 796. 子矩阵的和 - 二维前缀和
输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数:x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数n， m，q。
接下来n行，每行包含m个整数，表示整数矩阵。
接下来q行，每行包含四个整数x1,y1,x2,y2，表示一组询问。
输出格式
共q行，每行输出一个询问的结果。
数据范围
1≤n, m ≤1000, 1≤q≤200000, 1≤1 ≤2 ≤n，1≤91≤J2≤m,
-1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例：
17
27
21 
用容斥原理推出公式；
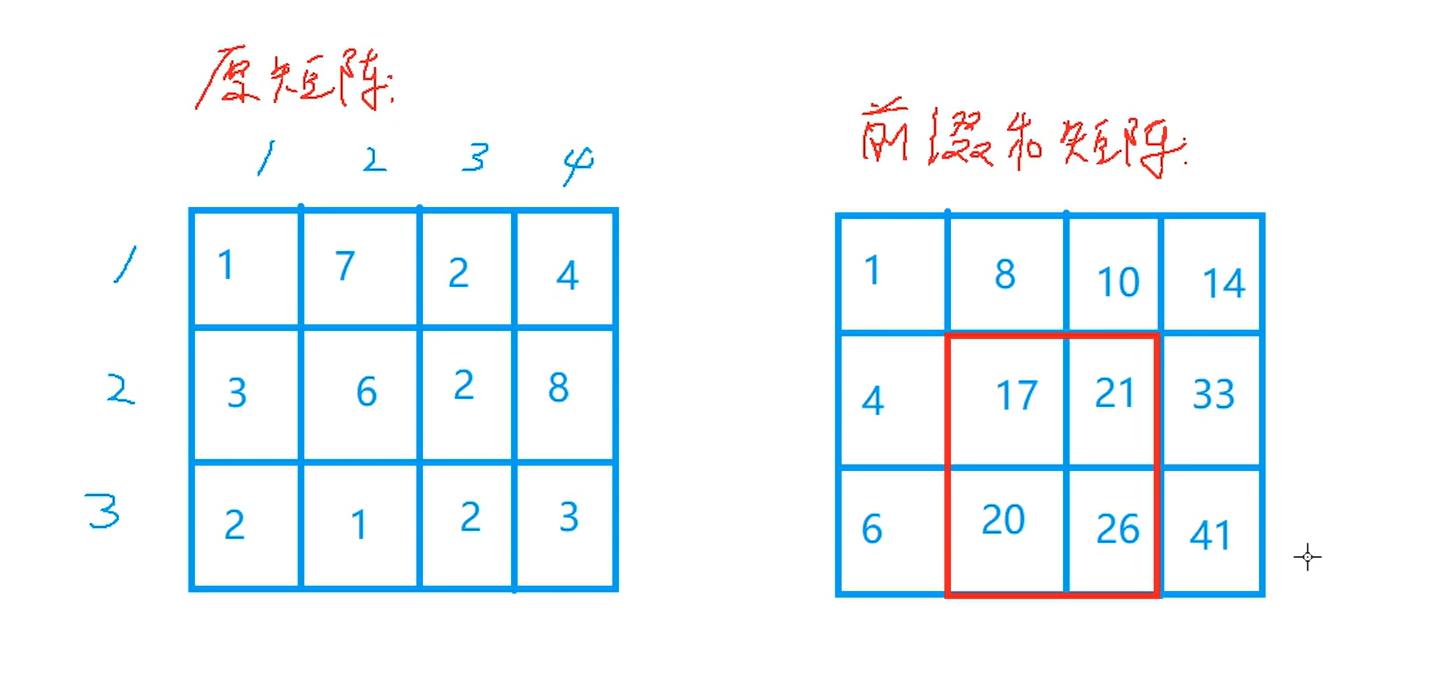
首先算出每一个坐标的前缀和s [ i ] [ j ]，在前缀和矩阵中再用一次容斥原理
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m, q;
int a[N][N], s[N][N];
int main()
scanf("%d%d%d", &n, &m, &q);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
scanf("%d", &a[i][j]);
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
while (q -- )
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
printf("%d\\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
return 0;
AcWing 797. 差分
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1差分思路：
首先给定一个原数组a：a[1], a[2], a[3],,,,,, a[n];
然后我们构造一个数组b ： b[1] ,b[2] , b[3],,,,,, b[i];
使得 a[i] = b[1] + b[2 ]+ b[3] +,,,,,, + b[i]
即：
a[0 ]= 0;
b[1] = a[1] - a[0];
b[2] = a[2] - a[1];
b[3] =a [3] - a[2];
........
b[n] = a[n] - a[n-1];
a数组是b数组的前缀和数组，比如对b数组的b[i]的修改，会影响到a数组中从a[i]及往后的每一个数。
首先让差分b数组中的 b[l] + c ,a数组变成 a[l] + c ,a[l+1] + c,,,,,, a[n] + c;
然后我们打个补丁，b[r+1] - c, a数组变成 a[r+1] - c,a[r+2] - c,,,,,,,a[n] - c;
核心操作：对差分数组b做 b[l] + = c, b[r+1] - = c（时间复杂度为O(1) ）
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
int main()
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]);
b[i] = a[i] - a[i - 1]; //构建差分数组
int l, r, c;
while (m--)
scanf("%d%d%d", &l, &r, &c);
b[l] += c; //将序列中[l, r]之间的每个数都加上c
b[r + 1] -= c;
for (int i = 1; i <= n; i++)
a[i] = b[i] + a[i - 1]; //前缀和运算
printf("%d ", a[i]);
return 0;
AcWing 798. 差分矩阵 - 二维差分
输入样例：
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例：
2 3 4 1
4 3 4 1
2 2 2 2思路与二维前缀和相似：
操作1、
b[x1][y1] + = c;
b[x1,][y2+1] - = c;
b[x2+1][y1] - = c;
b[x2+1][y2+1] + = c;
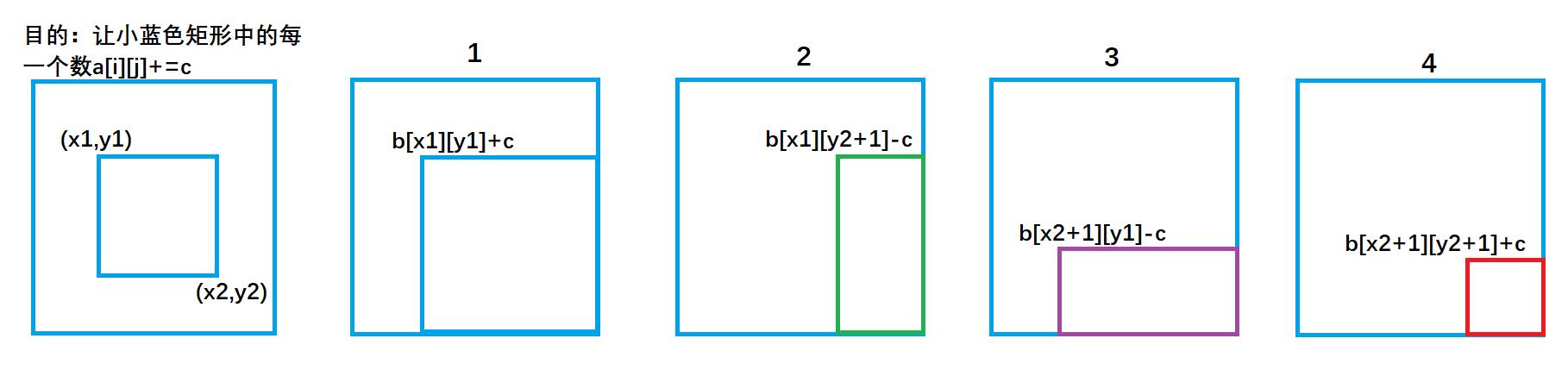每次对b数组执行以上操作，等价于：
for(int i=x1;i<=x2;i++)
for(int j=y1;j<=y2;j++)
a[i][j]+=c;操作2、
我们每次让以(i,j)为左上角到以(i,j)为右上角面积内元素(其实就是一个小方格的面积)去插入 c=a[i][j]，等价于原数组a中(i,j) 到(i,j)范围内 加上了 a[i][j] ,因此执行n*m次插入操作，就成功构建了差分b数组.
说白了，就是让c=a[i][j]，把操作1的方法用在一个空数组上，用n*m遍，操作完之后这个数组就是差分数组b[i][j]。
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
insert(i, j, i, j, a[i][j]); //构建差分数组AC代码：
#include <iostream>
using namespace std;
const int N = 1010;
int n, m, q;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
int main()
scanf("%d%d%d", &n, &m, &q);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
scanf("%d", &a[i][j]);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
insert(i, j, i, j, a[i][j]); //构建差分数组
while (q -- )
int x1, y1, x2, y2, c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert(x1, y1, x2, y2, c);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
//a[i]是差分数组b[i]的前缀和
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ ) printf("%d ", b[i][j]);
puts("");
return 0;
蓝桥杯算法竞赛系列第四章——二分算法
欢迎回到：遇见蓝桥遇见你，不负代码不负卿！
目录
好久不见啦铁汁们，蓝桥杯更新咯，快来尝尝鲜叭。
【前言】：由于本章基础知识点不多，所以笔者直接讲解四道典型题让大家感受一下二分法的美妙。
准备开始咯，坐稳哈...
引入：二分查找
【敲黑板】：用二分算法解题的前提是该数组有序！！！
【注意】：查找一次砍掉一半，效率非常高！但是条件比较苛刻，一定要有序！
题目描述
给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。
示例1：
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4示例2：
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
题解
设定左右指针
找出中间位置，并判断该位置值是否等于 target
nums[mid] == target 则返回该位置下标
nums[mid] > target 则右侧指针移到中间
nums[mid] < target 则左侧指针移到中间
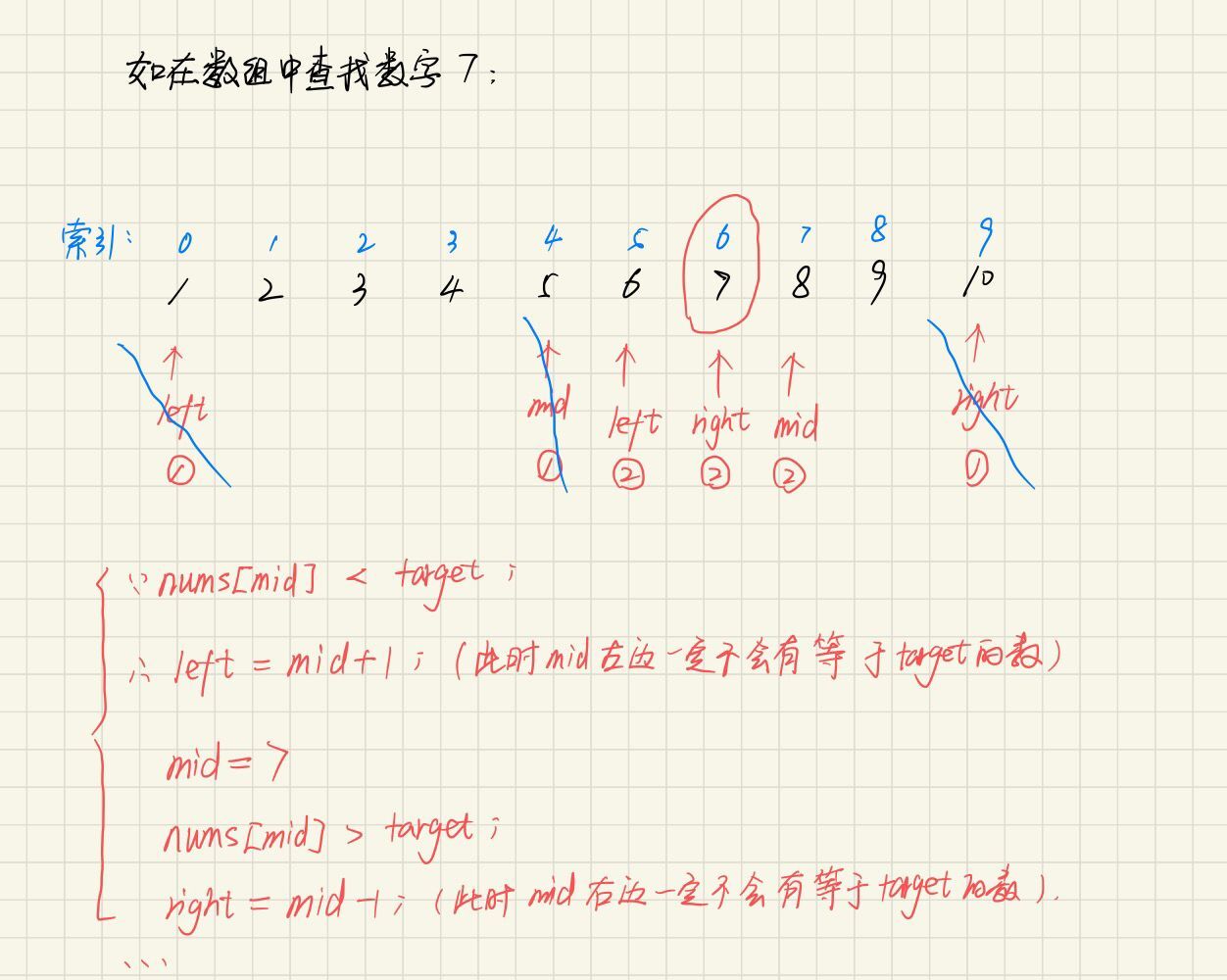
二分是一个比较简单的算法，只要大家记住上面这种套路就行啦。
代码执行
int search(int* nums, int numsSize, int target){
//考虑特殊情况
if(nums == NULL || numsSize == 0){
return -1;
}
int left = 0;//起始元素的索引
int right = numsSize - 1;//末尾元素的索引
int mid = 0;
while(left <= right){
//应该有很多人会写成mid = (left + right) / 2;这种写法不谨慎
//因为做的是加法运算，所以要考虑溢出的特殊情况
mid = left + (right - left) / 2;
if(nums[mid] < target){
left = mid + 1;
}else if(nums[mid] > target){
right = mid - 1;
}else{
return mid;
}
}
return -1;
}【注意】：while判断表达式中是left <= right, 为什么还要加上left == right 的情况呢，当二者相等的时候说明还有一个元素需要被比较，所以当left > right时停下来，因为此时中间已经没有元素需要被比较了。至于为什么将mid = left + (right - left) / 2; 的形式，上面代码中已经讲咯。
复杂度分析
时间复杂度：O(logN)
空间复杂度：O(1)
看，二分法是很高效的，大家在今后的训练中，如果遇到查找搜索类的题目要求时间复杂度是O(logN)的，要想到二分法哦。
好嘞，这就是二分查找，是不是很简单，下面再补充几道典型例题，让大家熟悉二分。
例题一：搜索插入位置
题目描述
给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
题目中要求使用时间复杂度为O(logN)的算法解题，所以结合本题题意，很容易就想到了二分法。
示例1：
输入: nums = [1,3,5,6], target = 5
输出: 2示例2：
输入: nums = [1,3,5,6], target = 7
输出: 4题解
- 整体思路和普通的二分查找几乎没有区别，先设定左侧下标 left 和右侧下标 right，再计算中间下标 mid
- 每次根据 nums[mid] 和 target 之间的大小进行判断，相等则直接返回下标，nums[mid] < target 则 left 右移，nums[mid] > target 则 right 左移
- 查找结束如果没有相等值则返回 left，该值为插入位置,注意哦，最后如果没有相等值，返回的是left
【注意】：
二分查找的思路不难理解，但是边界条件容易出错，比如 循环结束条件中 left 和 right 的关系，更新 left 和 right 位置时要不要加 1 减 1。这些都是大家自己动手画图理解，用代码去体会，只可意会不可言传哦。
代码执行
int searchInsert(int* nums, int numsSize, int target){
//考虑特殊情况
if(nums == NULL || numsSize == 0){
return -1;
}
int left = 0;
int right = numsSize - 1;
int mid = 0;
while(left <= right){
mid = left + (right - left) / 2;
if(nums[mid] > target){
right = mid - 1;
}else if(nums[mid] < target){
left = mid + 1;
}else{
return mid;
}
}
return left;
}复杂度分析
时间复杂度：O(logN)
空间复杂度：O(1)
是不是很简单，下面开始蹭加点难度咯，有点绕，需要仔细想哦，加油加油。
例题二：寻找峰值
题目描述
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例1：
输入：nums = [1,2,3,1]
输出：2
解释：3 是峰值元素，你的函数应该返回其索引 2。示例2：
输入：nums = [1,2,1,3,5,6,4]
输出：1 或 5
解释：你的函数可以返回索引 1，其峰值元素为 2；
或者返回索引 5， 其峰值元素为 6。题解
【注意】：二分法解题的前提要求是有序的，这题看起来没说有序呀，那怎么还能用二分法呢，我们也不能先进行排序，因为会把索引打乱，那该怎么办呢，请朝后看...
描述这个规律就是：
- 规律一：如果nums[mid] > nums[mid+1]，则在mid之前一定存在峰值元素
- 规律二：如果nums[mid] < nums[mid+1]，则在mid+1之后一定存在峰值元素
代码执行
int findPeakElement(int* nums, int numsSize){
//考虑特殊情况
if(nums == NULL || numsSize == 0){
return -1;
}
int left = 0;
int right = numsSize - 1;
int mid = 0;
while(left <= right){
if(left == right){
return left;
}
mid = left + (right - left) / 2;
if(nums[mid] > nums[mid + 1]){
right = mid;//mid之前一定存在峰值元素
}else{
left = mid + 1;//mid+1之后一定存在峰值元素
}
}
return left;
}复杂度分析
时间复杂度：O(logN)
空间复杂度：O(1)
例题三：搜索二维矩阵
题目描述
编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：
每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。
也就是说，整个二维数组都是升序的。
示例1：
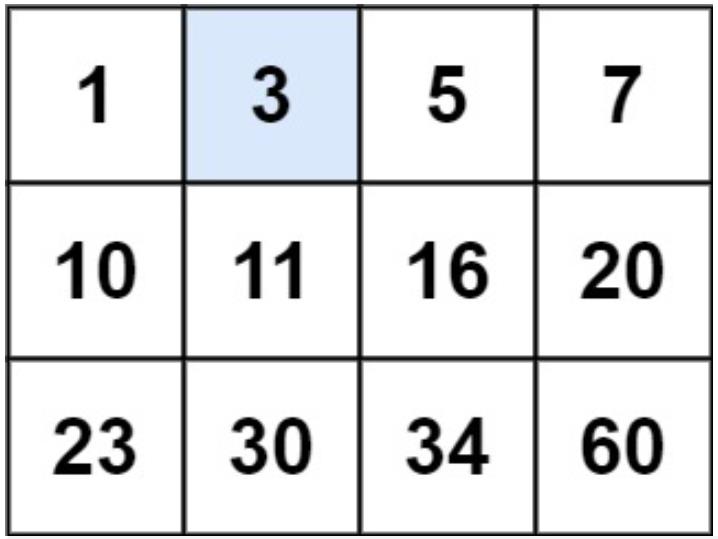
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true示例2：
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false题解
【注意】：本题的重点就在于一维索引和二维索引间的互换
代码执行
bool searchMatrix(int** matrix, int matrixSize, int* matrixColSize, int target){
//考虑特殊情况
if(matrix == NULL || matrixSize == 0){
return false;
}
int row = matrixSize;//行数
int col = *matrixColSize;//列数
int left = 0;//起始元素的索引
int right = row * col - 1;//最后一个元素的索引
int mid = 0;
int element = 0;
while(left <= right){
mid = left + (right - left) / 2;
element = matrix[mid / col][mid % col];//将一维的索引化成二维的索引
if(element == target){
return true;
}else if(element > target){
right = mid - 1;
}else{
left = mid + 1;
}
}
return false;
}复杂度分析
时间复杂度：O(logM*N), M,N分别是矩阵的行数和列数
空间复杂度：O(1)
好喽，铁汁把上面四道题目练习一遍，肯定就能对二分算法有一定的认识，加油加油哦。
思考题
大家先将上篇博文（分治算法）看一下，现在讲解那道留下的思考题。
蓝桥杯算法竞赛系列第三章——细谈递归的bro分治_安然无虞的博客-CSDN博客
最大子序和
题目描述
给定一个整数数组，找到一个具有最大和的连续子数组（子数组中至少包含一个数），要求返回其最大和。
注意：本题要求的是连续的子数组，可能有的题目要求可以是断开的，但本题不是。
将数组nums由中点mid分为三种情况：
1. 最大子串在左边
2. 最大子串在右边
3. 最大子串跨中点，左右两边元素都有（理解上的难点）
lSum 表示 [l,r] 内以 l 为左端点的最大子段和
rSum 表示 [l,r] 内以 r 为右端点的最大子段和
mSum 表示 [l,r] 内的最大子段和
iSum 表示 [l,r] 的区间和
代码执行
struct Status {
int lSum, rSum, mSum, iSum;
};
struct Status pushUp(struct Status l, struct Status r) {
int iSum = l.iSum + r.iSum;
int lSum = fmax(l.lSum, l.iSum + r.lSum);
int rSum = fmax(r.rSum, r.iSum + l.rSum);
int mSum = fmax(fmax(l.mSum, r.mSum), l.rSum + r.lSum);
return (struct Status){lSum, rSum, mSum, iSum};
};
struct Status get(int* a, int l, int r) {
if (l == r) {
return (struct Status){a[l], a[l], a[l], a[l]};
}
int m = l + (r - l) / 2;
struct Status lSub = get(a, l, m);
struct Status rSub = get(a, m + 1, r);
return pushUp(lSub, rSub);
}
int maxSubArray(int* nums, int numsSize) {
return get(nums, 0, numsSize - 1).mSum;
}由于想让大家搞懂知识点，所以这里的题目可能用这种解法不是最优解，没关系，我会在后面的算法中补充到，在每日一题中也会涉及到。今天就不布置思考题咯，铁汁们好好把上面题目自己尝试做出来。
蓝桥结语：遇见蓝桥遇见你，不负代码不负卿！
嘿嘿，期待铁汁们留言点评，如果能够再动动小手，给博主来个三连那就更好啦，您的认可就是我最大的动力！求求啦~~
以上是关于蓝桥杯AcWing 题目题解 - 二分与前缀和差分的主要内容，如果未能解决你的问题，请参考以下文章