神经网络 学习心得 笔记

Posted 2022-08-02 ML--小小白

第5章 神经网络 学习心得

神经元模型

神经元（neuron，亦称unit）其实就是一个小型的分类器，其将从其他神经元输入的信息带权重连接进入，然后比较其与阈值的相对大小，并将差异通过激活函数（activation function），决定其是否被”激活“/”兴奋“。这种神经元的抽象模型1943年就被提出了，被两位提出者名字首字母命名为”M-P神经元模型“。
最常使用的激活函数为Sigmoid（亦称squashing）函数。

感知机与多层网络

感知机（perceptron）

可以认为是一个很简单的线性分类器，找到一个线性可分数据中的分离超平面。从神经网络的角度，就是输入层直接到输出层，没有hidden layer，只有输出层含有神经元功能，因此也被称为阈值逻辑单元（threshold logic unit）。从简洁角度，可以把阈值项并入权重矩阵以及相应地输入特征增加一维（1/-1）。
感知机学习过程中，利用错误分类样本进行权重的更新，公式为：
$$\begin{array}{c}{w}_i\leftarrow w_i+\Delta w_i\\ \Delta w_i=\eta (y-\hat{y})x_i\end{array}$$
其中，可充分利用类标记为0或1的特点，将误分类点本来激活函数内宗量值正负性做个修正，从而将其作为“损失”，从而可以定义损失函数，求梯度方向的反方向为更新方向，当然这个可以发现，并不保证损失函数是严格的凸函数，因此其具有初值敏感的特点，最终的分离超平面并不会一致收敛。
Anyway，最为形象不公式化的直觉可以这样想：对权重的改变量，要使其尽量与输入的x向量内积后接近真实的y，所以就将真实的y相对于$\hat{y}$的差距补到宗量上去即可，同时内积的各个分量是x自身，因此一定为正，保证补的方向正确，但是这里并不精确计算到底该补多少，因此加个学习率，试探性的，补一补再看看是否已经正确分类了，直至把所有样本分开为止。

多层神经网络（multi-layer neural network）

只要包涵一个隐藏层，也就是至少两层有功能的M-P神经元，就可称为多层神经网络。

多层前馈神经网络（multi-layer feedforward neural network）

一般常见的神经网络的形式（至少目前小白阶段很常见），每层神经元与下一层神经元全互联（所以至少有两层神经元层），神经元同层不存在连接，不存在跨层连接，这种神经网络称为多层前馈神经网络。

误差逆传播算法(error BackPropagation，简称BP算法)

即通常所说的反向传播，利用梯度实现损失的最小化方法，在求梯度时，按照神经网络的反方向从损失函数出发，逐级向前求导数，因为逐级求导过程中，只涉及较为简单的运算，因此可以很快计算出，网络中某个位置的梯度实际上按照链式法则，就是该处神经元输出值对于输入或参数（weights）的梯度，再乘上后面神经元对于该输出的梯度，可认为是本地梯度（local gradient）与前级梯度的乘积。
标准的BP算法，每次利用一个样本，进行参数更新，类比随机梯度下降（SGD），对应的有梯度下降，标准BP对应的是累积BP算法，即累积误差反向传播算法。就是将整个训练集读取一遍以后（称为一个epoch或一个round），得到累积误差（损失的平均），再进行参数更新。
BP算法根据计算出的梯度，再结合学习率，进行参数（weights）更新，
$$\Delta w_{hj}=-\eta \frac{\partial E_k}{\partial w_{hj}}$$
直到达到收敛条件。由于前馈神经网络等神经网络其足够强大，很容易出现过拟合（BP只是一种实现收敛的算法，过拟合还是因为神经网络本身的复杂度可以足够高），实际中通常的一种策略是将数据集分为训练集和验证集，当验证集的错误率开始增加，表示泛化能力开始下降，就停止参数的更新（称为“早停”，early stopping），选择验证集和训练集错误率都较小的参数模型；另一种则是加入正则化项，比如：
$$E=\lambda \frac{1}{m}\sum _{k=1}^m{E}_k+(1-\lambda )\sum _i{w}_i^2$$
其中$E_k$表示第k类的误差。

全局最小（global minimum）与局部最小（local minimum）

如其名，全局最小就是整个损失函数全函数范围的最小值点，局部就是其与邻近点相比较，是最小值，没啥可说的。关键就是由于神经网络的复杂性，损失函数关于参数并不是严格凸函数，因此收敛到局部最小也很正常，此时梯度为0，停止更新。因此，关键问题是如何克服进入局部最小，通常有三种办法。第一种是使用不同的参数初值，因为这种问题一般都是初值敏感的，所以更换不同初值可以收敛到不同的局部最小，从中选取最小的作为全局最小；第二种是使用模拟退火（simulated annealing）算法，每次都有一定概率接受比当前更差的更新结果，从而可以跳出局部最小，同时概率要随着时间衰减，从而避免振荡不收敛；第三种是使用随机梯度下降，因为单个样本的贡献有时具有一定的随机性，在陷入局部最小时也可能由于一些个别样本的贡献使得更新step不为0。

其他神经网络

书中介绍了其他一些很著名的神经网络，但是都不详细，之后要找地方好好学习一下各个基础的网络，这里只能先观其大略了。

RBF网络（Radial Basis Funtion）

径向基函数网络，其中径向基函数作为神经元的激活函数，径向基函数衡量的是两个向量的“距离”，最常用的RBF是高斯径向基函数：
$$\rho \left(\mathbf{x},{\mathbf{c}}_i\right)=e^{-{\beta }_i{\Vert \mathbf{x}-{\mathbf{c}}_i\Vert }^2}$$
RBF网络是一个种单隐层网络，输出层没有激活函数，隐层没有线性部分，直接就是激活函数。理论证明，只要有足够多的隐层神经元，就可以任意精度逼近任意连续函数。
RBF训练分两步，第一步是去定径向基函数的中心，也就是被比较的向量，也可以说确定神经元的中心，通常采用随机采样、聚类方法获得；第二步是利用BP算法确定输出层线性部分和隐层高斯RBF（决定分布胖瘦的参数）部分的参数。

ART网络（Adaptive Resonance Theory）

自适应谐振理论网络，是一种竞争型学习策略的神经网络，所谓竞争型学习（competitive learning）策略，就是在神经元层中，各个神经元相互竞争，最终只有一个胜出，赢者通吃（winner-take-all），被激活，其他神经元被抑制的策略。
ART网络由比较层、识别层、识别阈值和重置模块构成，输入的样本由比较层接受，传递给识别层，识别层神经元数目可在训练时动态增加，识别层首先采用竞争策略选出与输入向量最相似的神经元权值向量，然后将其与识别阈值比较，如果大于表明足够相似，样本归入该权值向量代表的类别，且更新该神经元权值，使得其遇到与该样本类似的向量时，有更大的“相似度”。当相似度小于识别阈值，那么就重置增加一个以该样本为权值向量的神经元。显然，识别阈值越大，分类越精细，反之越粗略，同时这种网络的有点就是可以进行增量学习（incremental learning），即可以根据新加入的样本进行学习，而无需重新训练整个数据集，且之前的学习成果不会被抹除。或者也可以说，可以进行在线学习（online learning），即每获得一个样本更新一次模型，所以在线学习是增量学习的特例，增量学习是在线学习的批量模式（batch-mode）。
这种学习过程中也学习网络结构（增加神经元）的方式，也称为结构自适应网络或构造性（constructive）神经网络。

SOM网络（Self-Organizing Map，自组织映射）

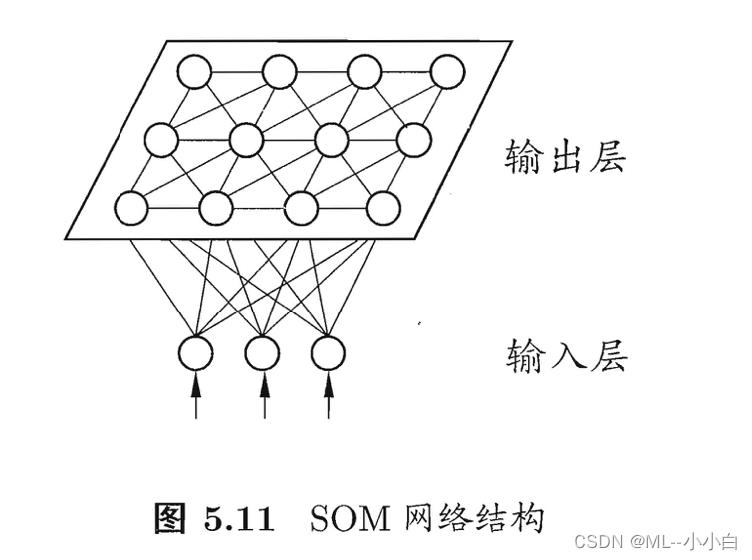
也称为自组织特征映射（Self-Organizing Feature Map)或Knhonen网络。也是一种竞争型无监督学习网络，它将高维数据映射到低维空间，通常为2D，并尽量保持高维空间拓扑结构，即将高维空间中距离近的点，映射到低维空间距离近的神经元上。SOM网络的输出层为排列为二维矩阵的神经元阵列，SOM输入样本传递到这层输出层后，权值向量与传递进来的向量最近的将会胜出，称为最佳匹配单元/神经元（best matching unit），并将其权值更新，从而遇到类似输入时更有优势地胜出。直至收敛。

级联相关网络（Cascade-Correlation）

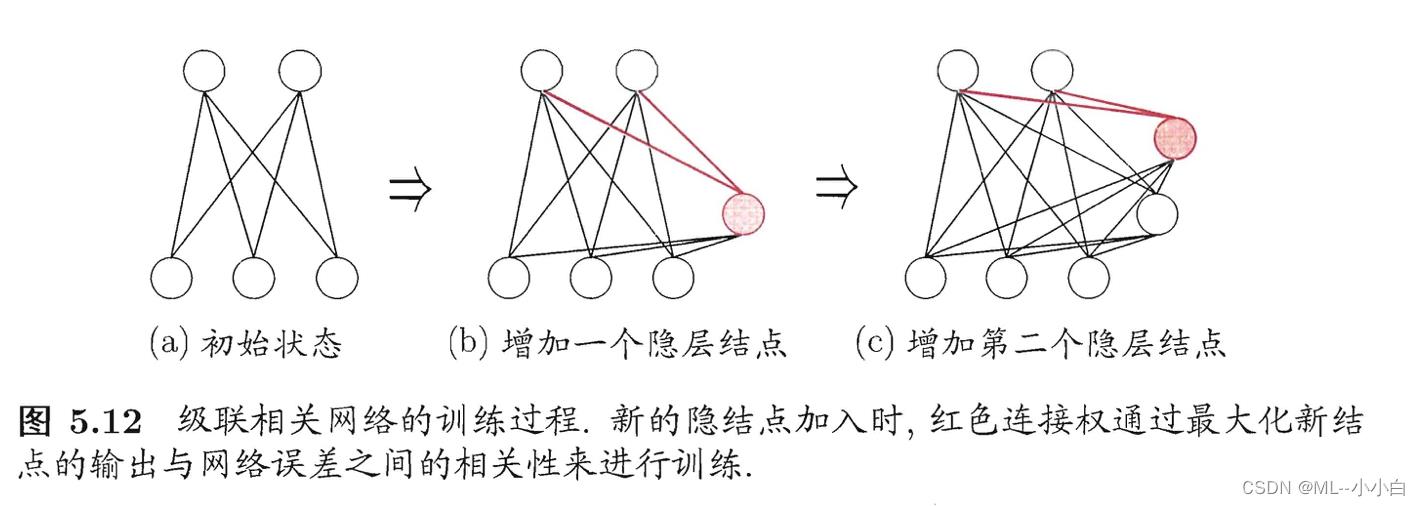
是一种结构自适应网络，不止学习参数，还学习神经网络的结构。级联是指建立层次连接结构，训练初始只有输入和输出层，是最简单的拓扑结构网络，训练中逐渐加入神经元，逐步建立起层次结构，新神经元加入后，其线性部分的权值是固定的。然后是相关，调整经过新神经元后到达输出层后，输出层线性部分的参数，使得最终的输出与网络的误差更相关。

Elman网络

递归神经网络（recurrent neural networks，or recursive neural networks），允许网络中出现环形拓扑结构，将神经元输出作为反馈，反馈回已经经历的神经元中。训练时，通过推广的BP算法进行。

Boltzman机

本质是一种递归神经网络，为网络定义一个能量，能量最小时达到理想状态，因此也被称为一种基于能量的模型（energy-based model）。这个就联想一下热力学，玻尔兹曼做出了很多贡献，能量越低越稳定越偏好，也是物理学很基本的概念。

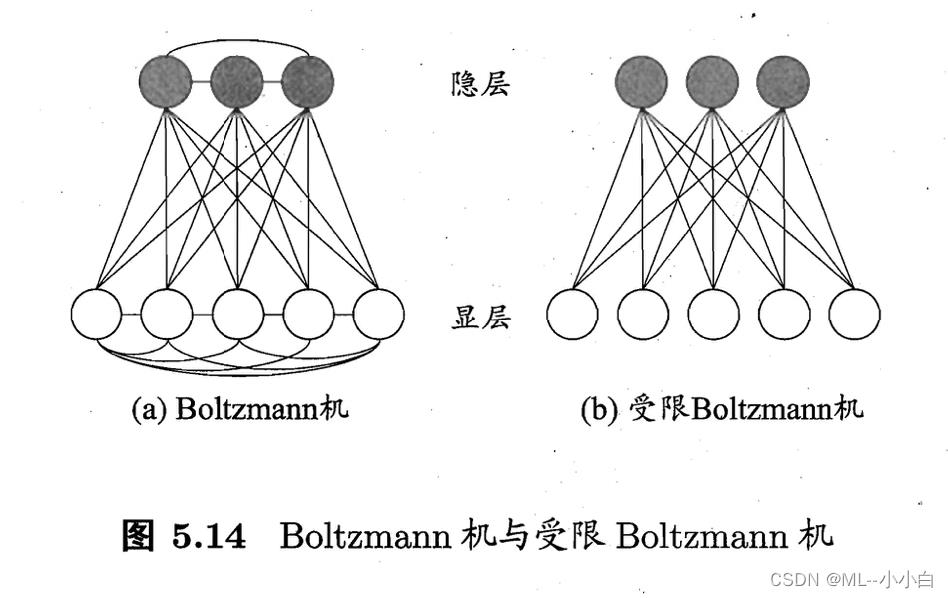
网络分为两层，显层用于表示数据的输入与输出，隐层可以理解为数据的内在表达，神经元只有0或1两种状态，其中1表示激活，0表示抑制，$s_i$表示第i个神经元的状态，$
\\theta_i$表示其阈值。能量包括自能和互能（只考虑连接的最近邻）：
$$E(s)=-\sum _{i=1}^{n-1}\sum _{j=i+1}^n{w}_{ij}{s}_i{s}_j-\sum _{i=1}^n{\theta }_i{s}_i$$
网络以不依赖输入值顺序的方式进行更新，最终达到Boltzmann分布，此时各个状态组成的状态向量的概率仅有能量决定：
$$P(s)=\frac{e^{-E(s)}}{{\sum }_t{e}^{-E(t)}}$$
训练的逻辑就是使样本对应的状态向量能量更低，出现概率更大，标准Boltzman是全连接图，复杂度很高，通常使用受限Boltzmann机（Rsetricted
Boltzmann Machine， RBM），仅保留显层与隐层的连接。
玻尔兹曼机使用对比散度（Contrastive Divergence，简称CD）进行训练，令$\mathbf{v}$和$\mathbf{h}$分别为显层与隐层的状态向量，则层内的神经元概率分布可写为：
$$\begin{array}{l}P(\mathbf{v}\mid \mathbf{h})={\prod }_{i=1}^{d}P\left(v_i\mid \mathbf{h}\right)\\ P(\mathbf{h}\mid \mathbf{v})={\prod }_{j=1}^{q}P\left(h_j\mid \mathbf{v}\right)\end{array}$$
CD算法首先由上面的概率分布和输入样本$\mathbf{v}$得到$\mathbf{h}$然后，再由$\mathbf{h}$生成${\mathbf{v}}^{\prime }$，接着得到 h ′