24基于原型的切比雪夫低通滤波器设计理论（插入损耗法）

Posted 2023-03-29 怡步晓心l

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了24基于原型的切比雪夫低通滤波器设计理论（插入损耗法）相关的知识，希望对你有一定的参考价值。

24、基于原型的切比雪夫低通滤波器设计理论（插入损耗法）

基于原型的滤波器设计是设计的一个基础的方法，虽然在现在有更加强大的自动化工具能够取代它，但是如果要进行理论研究仍需要对其有所了解。

写此文的初衷并非是介绍切比雪夫低通滤波器设计理论，而是发现国内有一些文章把低通滤波器网络和低通滤波器匹配网络混为一谈。使用低通滤波器网络的设计原型进行低通滤波器匹配网络的设计。

低通滤波器匹配网络其实就是在滤波的基础上增加了一个阻抗变换的作用，其设计参数包含阻抗变换比、设计带宽参数等等，因为其良好的匹配特性所以经常使用在功率放大器的设计之中。如MTT文章：
Design of Highly Efficient Broadband Class-E Power Amplifier Using Synthesized Low-Pass Matching Networks

下面先对基于原型的切比雪夫低通滤波器设计理论（插入损耗法）进行介绍，并介绍使用等效原理将其转换为微带线电路。

1 插入损耗法介绍

插入损耗法看似非常高大上，其实对于设计者而已就是一个简单的查表过程，大家可以参考文章：
插入损耗法设计低通原型滤波器（二）：等波纹低通滤波器设计
在此也再次进行举例说明，设计的参数如下所示：
1、截止频率：3.8GHz
2、带内波纹：0.5dB
3、在7.6GHz时衰减达60dB以上

2 插入损耗法根据设计要求查表

插入损耗法设计的第一步就是根据带内波纹要求进行查表，此处带内波纹的要求为小于0.5dB，找到如下的图表（切比雪夫低通滤波器的元件数值表）：

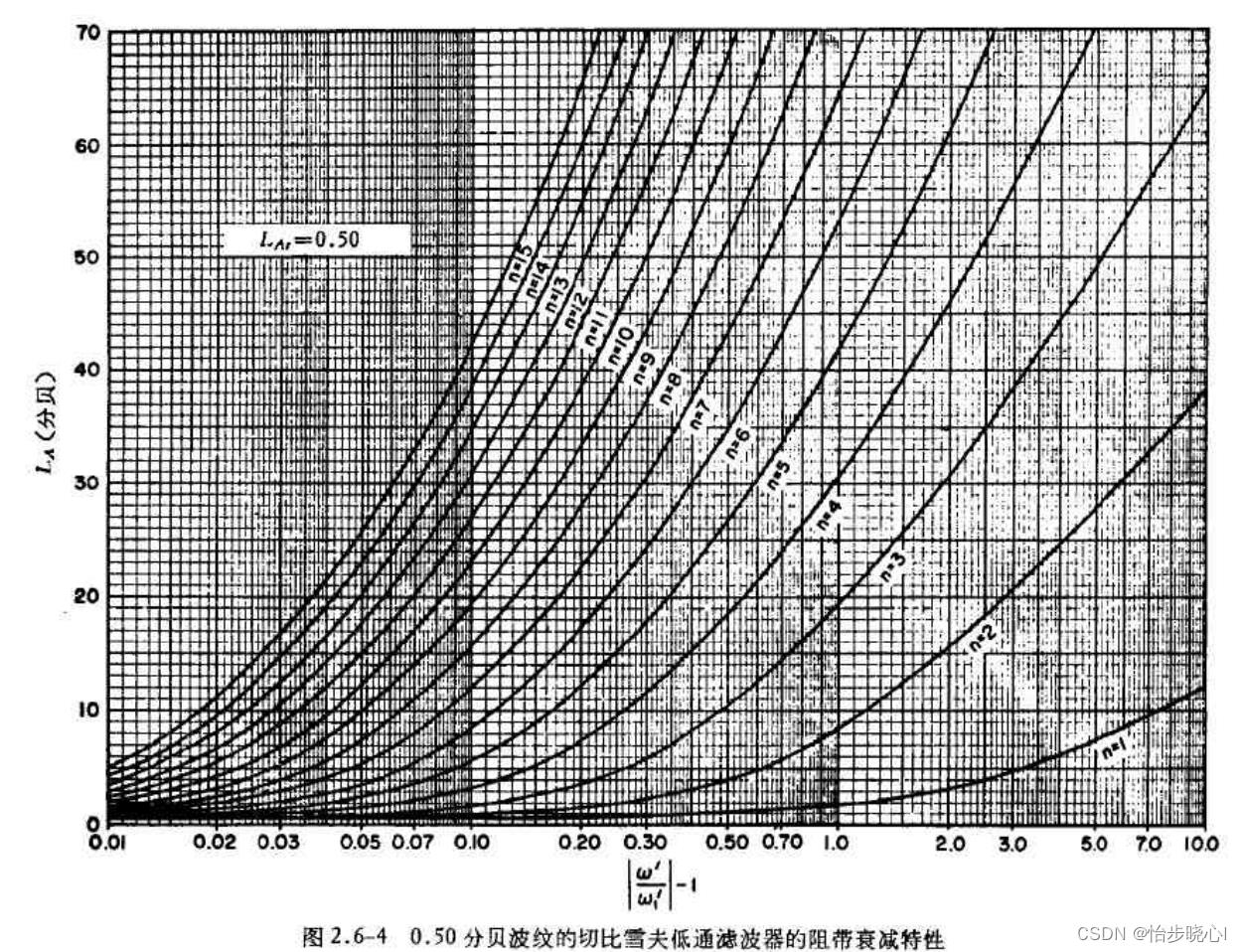
设计的要求是要在2f0=7.6时衰减达到60dB以上，此时的横坐标数值为（7.6/3.8-1）=1，也就是要在横坐标为1的时候衰减要在60dB以上。N要选择奇数，此时选择N=7。

下面需要更加N的数值和插入损耗的数值进行查表，查的表如下所示：

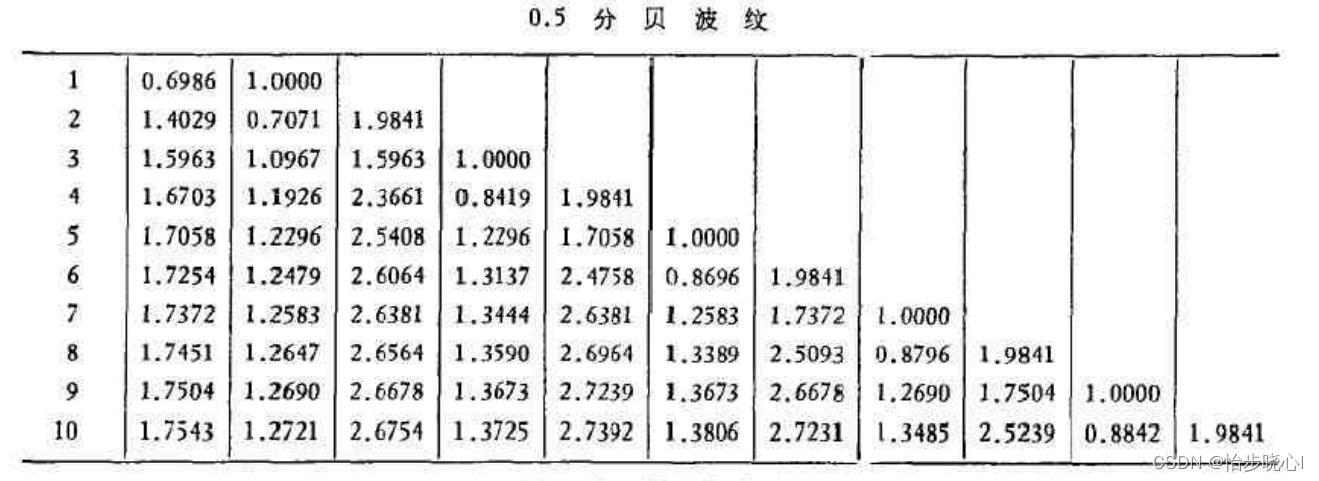
主要看N=7的时候的数值就行了，可以看到N=7时需要8个元器件，也就是4个电感和电容：

此处就可以得到设计的原型了。

3 基于原型设计集总参数滤波器

设计的转换原理可以参考：
Hong J S. Microstrip filters for RF/microwave applications[J]. IEEE Microwave Magazine,
2002, 3(3):62-65

此处直接放公式：

上面wc就是角频率，wc=2pif，Z0就是端口阻抗，一般设置为50欧姆即可，gc和gl就是查表得到的元器件，比如说上面查表得到的元器件的第一个为1.7372，如果你想要第一个是电感就使用第一个公式计算感抗，如果你想要第一个是电容就使用第一个公式计算容抗，这个是自己选择的。但是如果第一个是电感，第二个就一定是电容，第三个也一定是电感，由此类推。
为了方便大家计算，我写了一个Matlab代码：

clear all
clc
f=3.8e9;%设置截止频率
Z0=50;%设置端口阻抗
g=1.7372;


L=Z0*g/(2*pi*f);
C=g/(Z0*2*pi*f);
disp(['如果是电感，电感值为：',num2str(L*1e9),'nH'])
disp(['如果是电容，电容值为：',num2str(C*1e12),'pF'])

此处设计的时候我采用第一个是电感的模式，第一个的参数g为1.7372，赋值并计算得到如下结果：

因为是电感，此处得到的电感值为3.6379nH，因此开头的第一个电感值就是3.6379nH。依次代入不同的g计算其他集中参数的数值，得到如下的电路图：

运行仿真得到S参数结果，可以看到通带的波纹不满足要求，但是阻带衰减达到了70dB，此处仅是示范就不进行微调了：

4 基于原型设计分布式参数滤波器

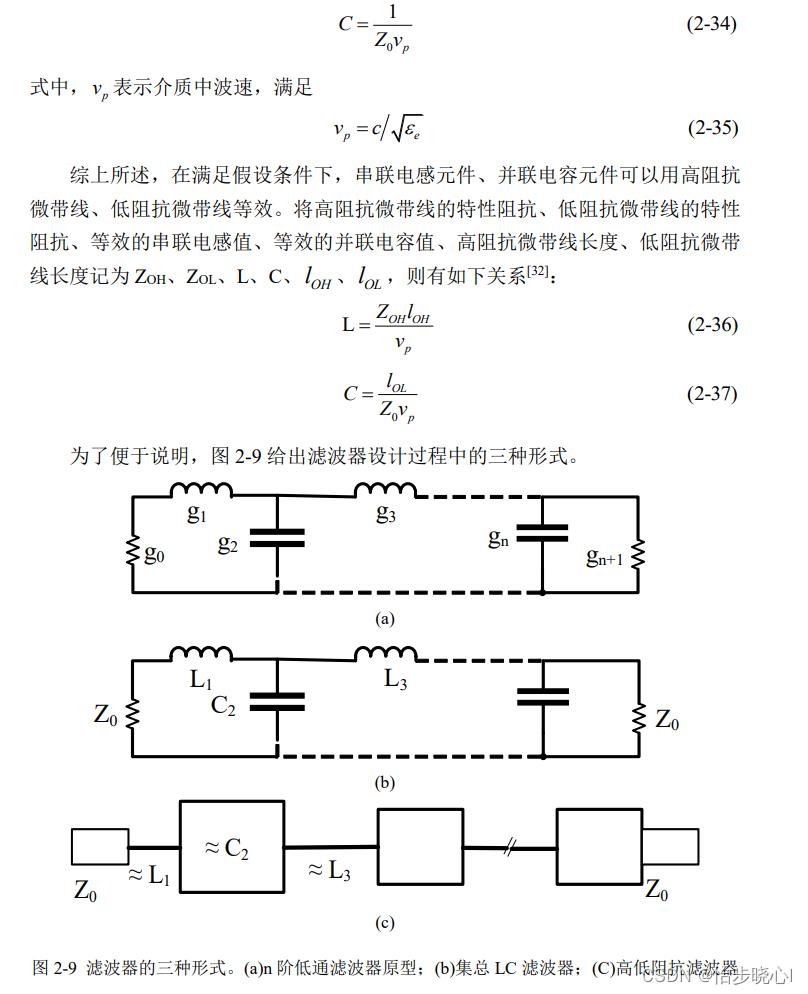
基于原型可以设计分布式参数的滤波器，比较常见的就是微带线滤波器。设计时需要用到一个十分重要的等效，此处参考其他论文的说明，简单来说就是用高低阻抗线进行等效，其中高阻抗微带线等效为电感，低阻抗微带线等效为电容：

为了方便计算，这边直接写成了Matlab代码：

clear all
clc
f=3.8e9;%设置截止频率
Z0=50;%设置端口阻抗
Zoh=90;%高阻抗线阻抗
Zol=20;%低阻抗线阻抗
epsilon=4.6;%设置板材介电常数


g=1.7372;


L=Z0*g/(2*pi*f);
C=g/(Z0*2*pi*f);


c=299792458;%光速

loh=L*c/(Zoh*sqrt(epsilon));
lol=C*Zol*c/sqrt(epsilon);


disp(['如果是电感，电感值为：',num2str(L*1e9),'nH，等效微带线长度为：',num2str(loh*1e3),'mm'])
disp(['如果是电容，电容值为：',num2str(C*1e12),'pF，等效微带线长度为：',num2str(lol*1e3),'mm'])

此处设计的时候我采用第一个是电感的模式，第一个的参数g为1.7372，赋值并计算得到如下结果，也代表第一个线的长度为5.6501mm：

可以依次计算其他参数的线长。其次需要得到线宽，此处使用的是FR4板材，介电常数为4.6，使用ADS计算工具LineCalc进行计算：

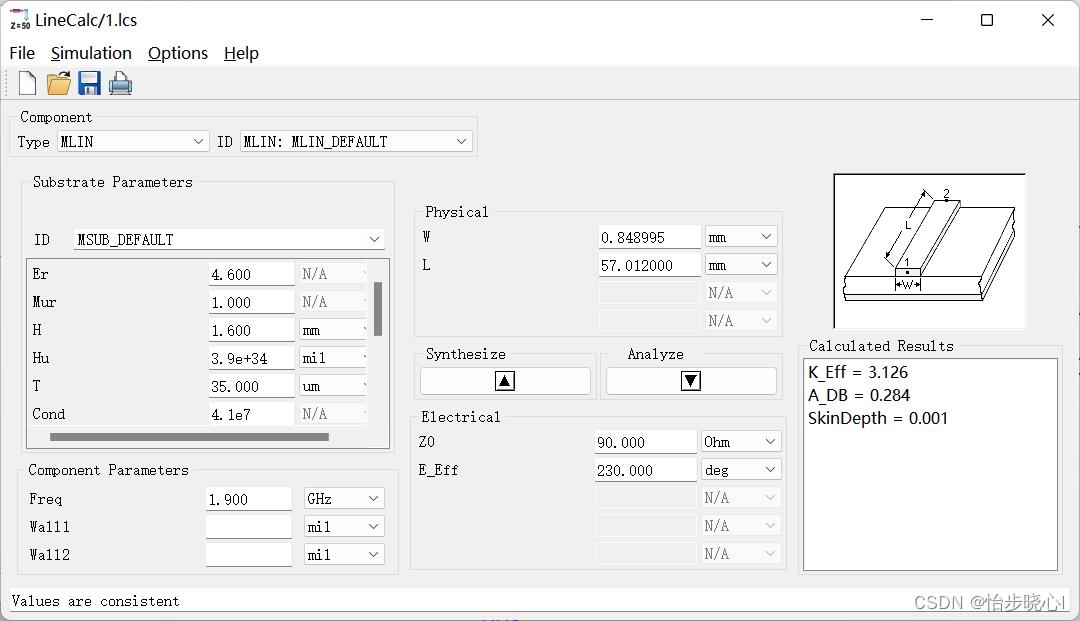
由此得到此板材下20欧姆的低阻抗线线宽为10.8mm，90欧姆的高阻抗线线宽为0.85mm左右，由此构建电路图如下所示：

运行仿真，得到结果：

可以看到基本满足设计要求，但是还需要进行调整，我这边以教学为主，就不进行微调了。
ADS也有便捷的基于这种方法的设计工具，参考之前的博文：
10、ADS使用记录之设计高低阻抗滤波器（含版图仿真）

基于切比雪夫逼近法的滤波器的matlab设计与实现

一、理论基础

二、核心程序

三、仿真测试结果

一、理论基础

从FIR数字滤波器的系统函数可以看出，极点都是在Z平面的原点，而零点的分布是任意的。不同的分布对应不同的频率响应，最优设计实际上就是调节这些零点的分布，使得实际滤波器的频率响应和理想滤波器的频率响应之间的最大绝对误差最小。

切比雪夫逼近法正是利用这种思想进行FIR数字滤波器设计的，对H作最佳逼近，因而获得了较好的通带和阻带性能，并能准确地制定通带和阻带的边缘，是一种更有效的设计方法。

前面已经介绍了切比雪夫逼近法的基本理论过程，这里将使用MATLAB进行FIR滤波器的设计与仿真。整个滤波器的设计步骤如下：

最后按如下的式子：

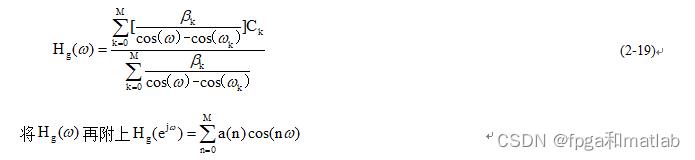
二、核心程序

clc;
clear;
close all;

select = 2;%1：进行普通信号测试；2：音乐信号的测试


if select == 1
%普通信号测试
source = func_test_signal();
figure;
subplot(121);plot(source):title('原始音乐信号');
f     =[0 0.25 0.5 1]; %给定频率轴分点;
a     =[1 1 0 0];     %给定在这些频率分点上理想的幅频响应;
weigh =[1 10];         %给定在这些频率分点上的加权;
y=fftshift(abs(fft(source)));

subplot(122);plot(y);title('原始信号的频谱');

figure;
b=remez(10,f,a,weigh);%设计出切比雪夫最佳逼近滤波器;
[h,w]=freqz(b,1,512,1);%数字滤波器的频率响应;
h=abs(h);%绝对值;
h=20*log10(h);
subplot(121)%改置定位坐标系;
stem(b,'.');
grid;
title('切比雪夫逼近滤波器的抽样值');
subplot(122);
plot(w,h);%生成参数方程的图形;
grid;
title('切比雪夫逼近滤波器幅频特性(dB)');
source2=filter(b,1,source);    %滤波正常实现
figure;
subplot(121);plot(source2):title('通过切比雪夫逼近法滤波后的音乐信号');
y2=fftshift(abs(fft(source2)));
subplot(122);plot(y2);title('滤波后的信号频谱');
end


if select == 2
%音乐信号测试
[source,Fs,nbits] = wavread('source.wav');
figure;
plot(source):title('原始音乐信号');
f     =[0 0.4 0.6 1]; %给定频率轴分点;
a     =[1 1 0 0];     %给定在这些频率分点上理想的幅频响应;
weigh =[1 10];         %给定在这些频率分点上的加权;
y=fftshift(abs(fft(source)));
figure;
plot(y):title('原始信号的频谱');
sound(source,Fs);
figure;
b=remez(32,f,a,weigh);%设计出切比雪夫最佳逼近滤波器;
[h,w]=freqz(b,1,512,1);%数字滤波器的频率响应;
h=abs(h);%绝对值;
h=20*log10(h);
subplot(121)%改置定位坐标系;
stem(b,'.');
grid;
title('切比雪夫逼近滤波器的抽样值');
subplot(122);
plot(w,h);%生成参数方程的图形;
grid;
title('切比雪夫逼近滤波器幅频特性(dB)');
source2=filter(b,1,source);    %滤波正常实现
figure;
plot(source2);title('通过切比雪夫逼近法滤波后的音乐信号');
y2=fftshift(abs(fft(source2)));
figure;
plot(y2);title('滤波后的信号频谱');
sound(source2,Fs);
end