可变形卷积(Deformable Conv)原理解析与torch代码实现

Posted 2023-03-29 胖虎记录学习

1. 可变形卷积原理解析 

1.1 普通卷积原理

        传统的卷积操作是将特征图分成一个个与卷积核大小相同的部分，然后进行卷积操作，每部分在特征图上的位置都是固定的。

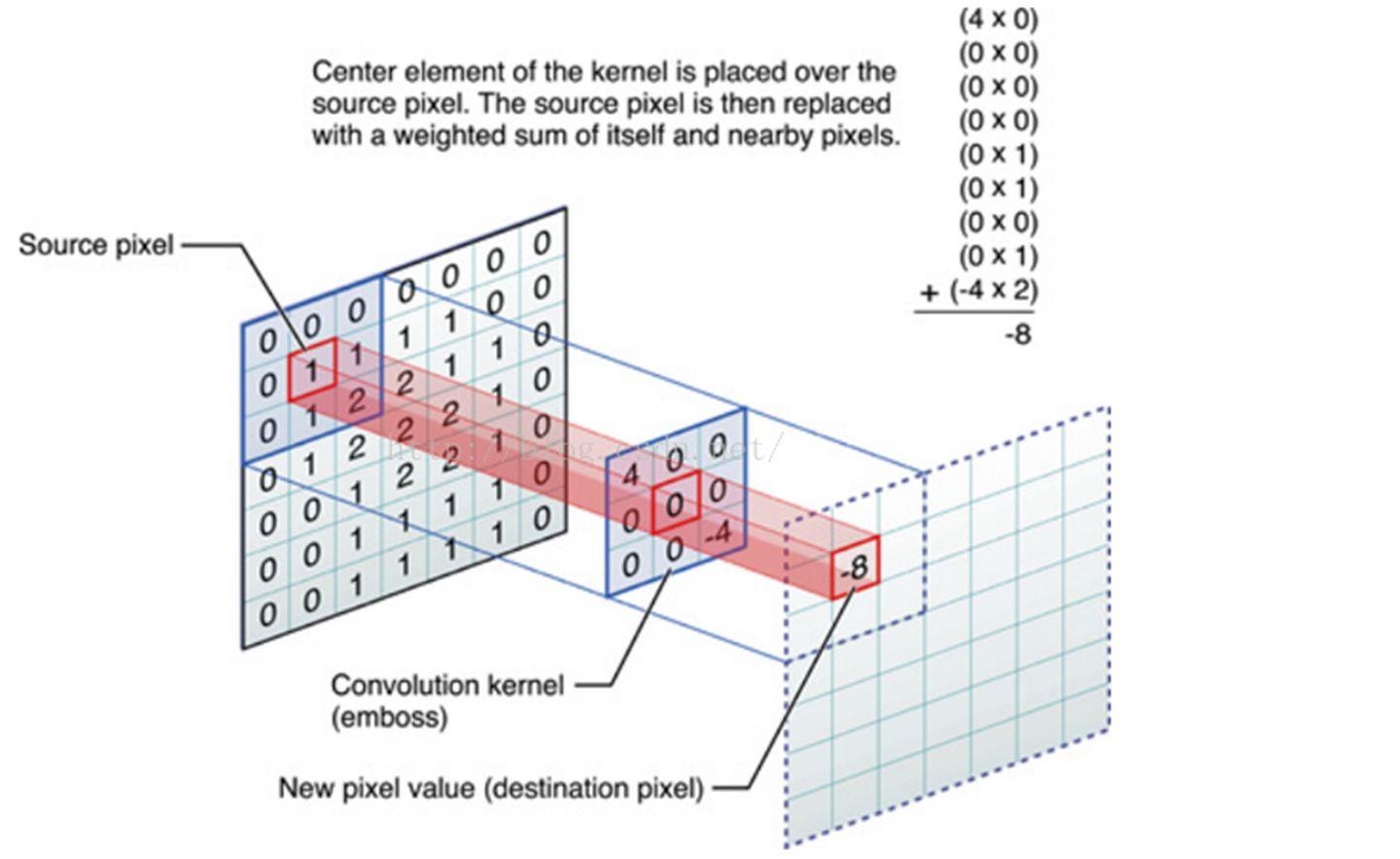
图1 普通卷积过程 

        图1所示为普通卷积在输入特征图上进行卷积计算的过程，卷积核大小为3*3，在输入特征图尺寸为7*7上进行卷积，将卷积核权重与输入特征图对应位置元素相乘并求和得到输出特征图元素，按一定方式滑动窗口就能计算得到整张输出特征图。

        因此，对于输入特征图上任意一点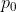，卷积操作可表示为： 

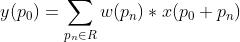
公式1 卷积操作公式 

        其中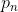，代表卷积核中每一个点相对于中心点的偏移量，可用如下公式表示（3*3卷积核为例）： 

    

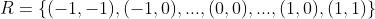
公式2 卷积核点相对偏移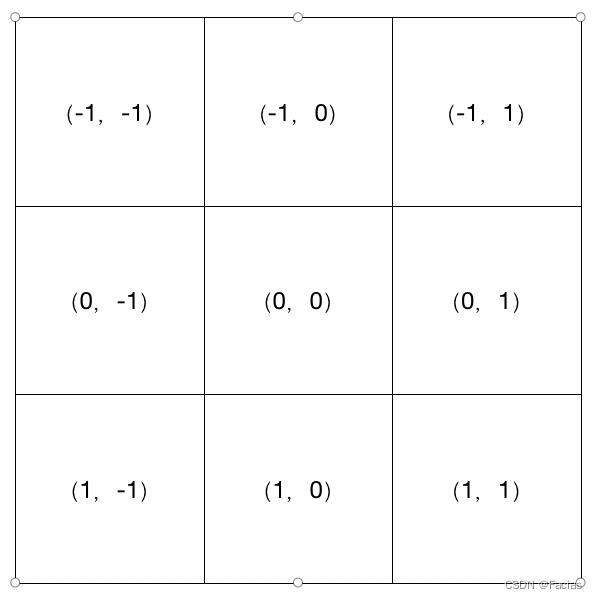

图2 3*3卷积核点相对偏移示例图

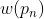 表示卷积核对应位置的权重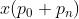，表示输入特征图上位置处的元素值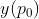，表示输出特征图上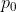位置的元素值，由卷积核与输入特征图进行卷积得到。

 1.2 可变形卷积思想

         常规卷积的卷积核为固定的大小与形状，对于形状规则的物体可能会有更好的效果，那如果遇到形变比较复杂的物体呢？

         一般来讲，可采用的做法有：丰富数据集、引入更多复杂形变的样本，使用各种数据增强和tricks，人工设计一些手工特征和算法等等，那么是否可以采用更加灵活的卷积核呢？于是可变形卷积--Deformable Conv出现了。

 先来一张图感受一下，图3为标准卷积与可变形卷积的卷积示例。

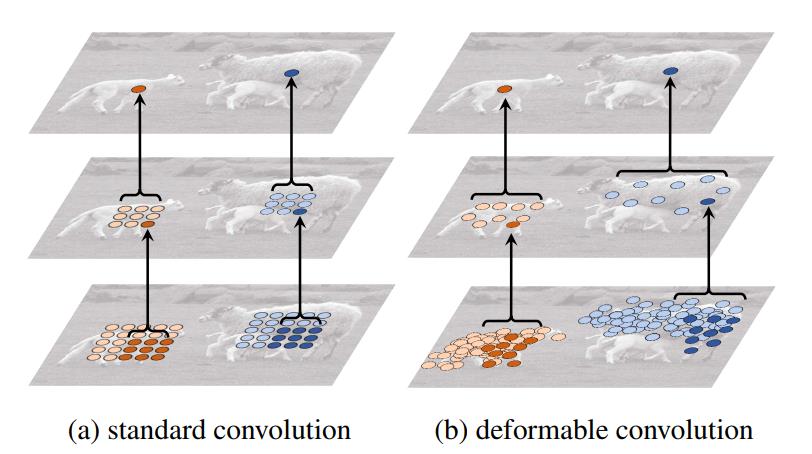
图3 标准卷积与可变形卷积的卷积示例 

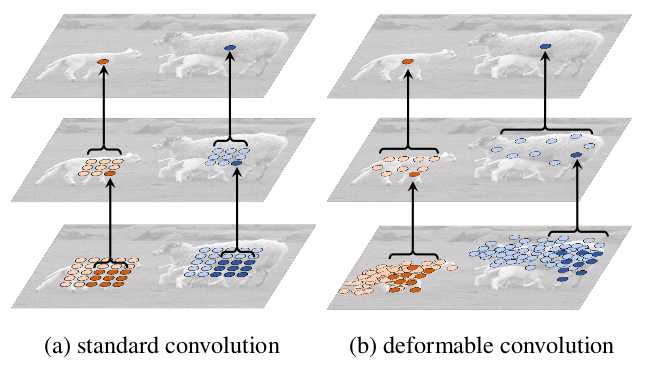
        通过左右对比可以明显的看出，可变形卷积的采样位置更符合物体本身的形状和尺寸，而标准卷积的形式却不能做到这一点。能够明显的看到可变性卷积顶层特征图中最终的特征点学习了物体的整体特征，这个特征只针对于物体本身，相比原始的卷积它更能排除背景噪声的干扰，得到更有用的信息。 

 1.3 可变形卷积原理

         从图2可以看出，可变形卷积的采样位置是可变的，或者说是可学习的，因此可变形卷积可以更好的考虑到物体形状变化。

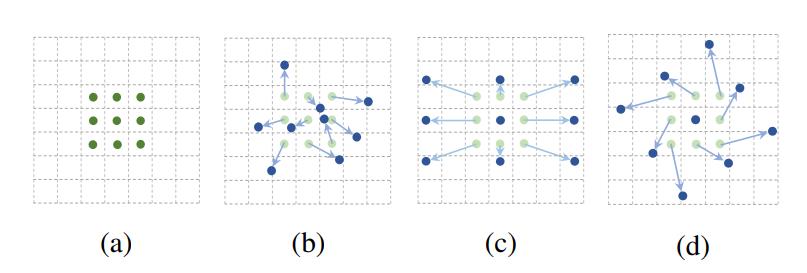
        图4 可变形卷积的不同采用点

        图4中（a）是常见的3x3卷积核的采样方式，（b）是采样可变形卷积，加上偏移量之后的采样点的变化，其中（c）(d)是可变形卷积的特殊形式。

        因此可形变卷积的原理是基于一个网络学习offset（偏移），使得卷积核在input feature map的采样点发生偏移，集中于我们感兴趣的区域或者目标。

        可变形卷积则在公式1的基础上为每个点引入了一个偏移量，偏移量是由输入特征图与另一个卷积生成的，通常是小数。 

 

公式3 可变形卷积操作公式 

        其中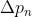， 表示偏移量。

        由于加入偏移量后的位置一般为小数，并不对应输入特征图上实际的像素点，因此需要使用插值来得到偏移后的像素值，通常可采用双线性插值，用公式表示如下：

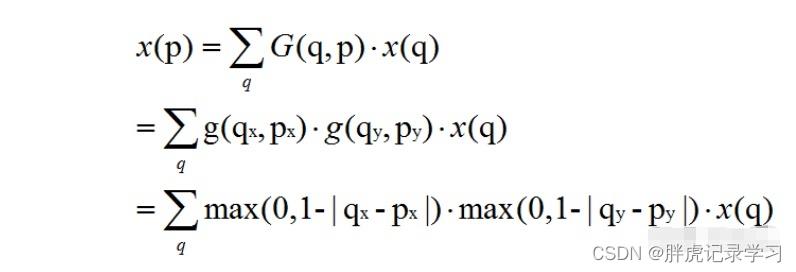
 公式4 双线性插值

        其中，公式中最后一行的max(0, 1-...)限制了插值点与邻域点不超过1个像素的距离。 

        双线性插值是指将插值点位置的像素值设为其4邻域像素点的加权和，邻域4个点是离其最近的在特征图上实际存在的像素点，每个点的加权权重则根据它与插值点横、纵坐标的距离来设置，最终得到插值点的像素值。

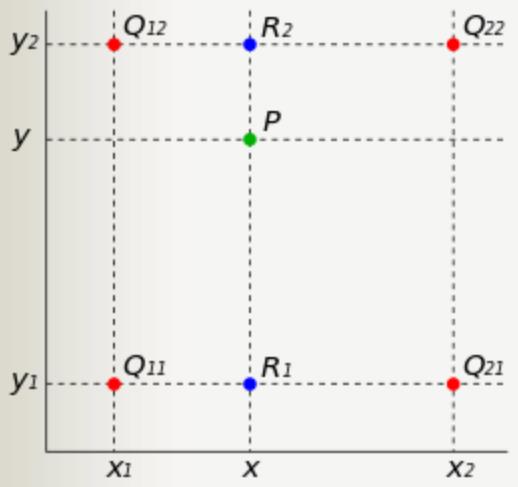
 图5 双线性插值示例图

        根据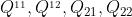4个点的加权和计算得到P点的像素值，各点权重由各点距离P点的距离确定。

1.4 可变形卷积

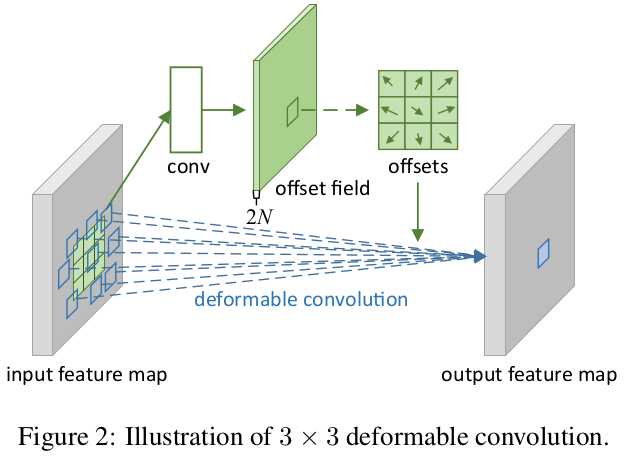
        图6为可变形卷积示意图。可以看到offsets（偏移）是额外使用一个卷积来生成的，与最终要做卷积操作那个卷积不是同一个 。图示N为卷积核区域大小，例如3*3大小的卷积核，N=9，图中绿色过程为卷积学习偏移的过程，其中offset field的通道大小为2N，表示卷积核分别学习x方向与y方向的偏移量。

        图6所示，在input feature map上普通卷积操作对应卷积采样区域是一个卷积核大小的正方形（绿框），而可变形卷积对应的卷积采样区域为一些蓝框表示的点，这就是可变形卷积与普通卷积的区别。

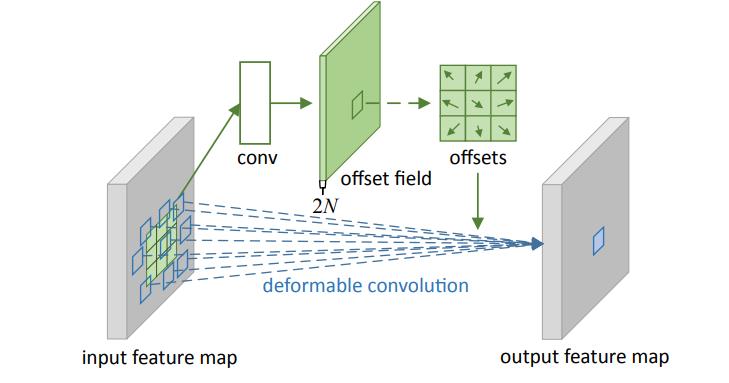
图6 可变形卷积示意图

        可变形卷积的具体细节：

1. 一个output feature map上的点对应到input feature map上的卷积采样区域大小为K*K，按照可变形卷积的操作，这K*K区域的每一个卷积采样点都要学习一个偏离量offset，而offset是用坐标表示的，所以一个output要学习2*K*K个参数。假设一个output大小为H*W，所以一共要学习2*K*K*H*W个参数。即上图的offset field(N=K*K)，其维度为B*2*K*K*H*W，其中B代表batch_size；
2. 假设input feature map的维度为B*C*H*W，一个batch内的特征图（一共C个）共用一个offset field，即一个batch内的每张特征图用到的偏移量是一样的；
3. 可变形卷积不改变input feature map的尺寸，所以output feature map也为H x W；

 2. 可变形卷积的实现

2.1 可变形卷积实现流程：

借鉴了博主Facias的代码实现逻辑图，具体实现看代码。

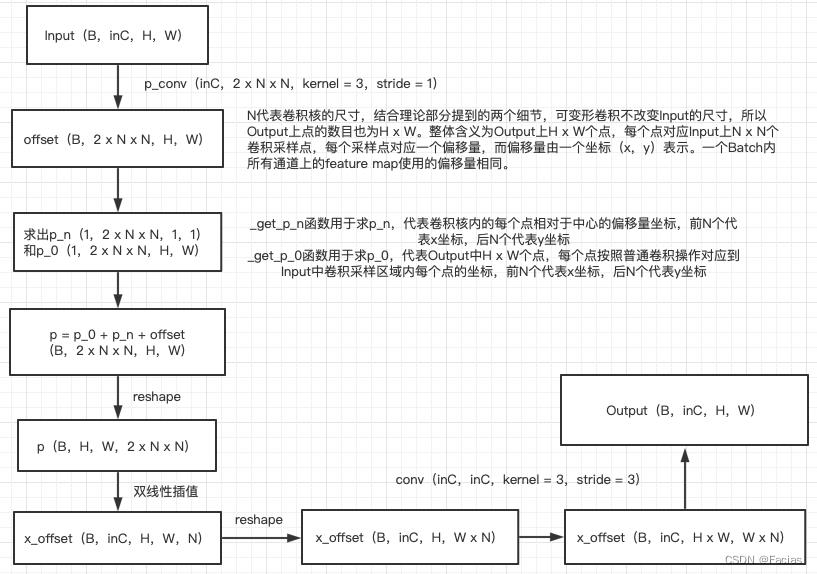
图7 可变形卷积实现流程 

 2.2 可变形卷积torch实现

class DeformConv2d(nn.Module):
    def __init__(self, inc, outc, kernel_size=3, padding=1, stride=1, bias=None, modulation=False):
        """
        Args:
            modulation (bool, optional): If True, Modulated Defomable Convolution (Deformable ConvNets v2).
        """
        super(DeformConv2d, self).__init__()
        self.kernel_size = kernel_size
        self.padding = padding
        self.stride = stride
        self.zero_padding = nn.ZeroPad2d(padding)
        # conv则是实际进行的卷积操作，注意这里步长设置为卷积核大小，因为与该卷积核进行卷积操作的特征图是由输出特征图中每个点扩展为其对应卷积核那么多个点后生成的。
        self.conv = nn.Conv2d(inc, outc, kernel_size=kernel_size, stride=kernel_size, bias=bias)
        # p_conv是生成offsets所使用的卷积，输出通道数为卷积核尺寸的平方的2倍，代表对应卷积核每个位置横纵坐标都有偏移量。
        self.p_conv = nn.Conv2d(inc, 2*kernel_size*kernel_size, kernel_size=3, padding=1, stride=stride)
        nn.init.constant_(self.p_conv.weight, 0)
        self.p_conv.register_backward_hook(self._set_lr)

        self.modulation = modulation # modulation是可选参数,若设置为True,那么在进行卷积操作时,对应卷积核的每个位置都会分配一个权重。
        if modulation:
            self.m_conv = nn.Conv2d(inc, kernel_size*kernel_size, kernel_size=3, padding=1, stride=stride)
            nn.init.constant_(self.m_conv.weight, 0)
            self.m_conv.register_backward_hook(self._set_lr)

    @staticmethod
    def _set_lr(module, grad_input, grad_output):
        grad_input = (grad_input[i] * 0.1 for i in range(len(grad_input)))
        grad_output = (grad_output[i] * 0.1 for i in range(len(grad_output)))

    def forward(self, x):
        offset = self.p_conv(x)
        if self.modulation:
            m = torch.sigmoid(self.m_conv(x))

        dtype = offset.data.type()
        ks = self.kernel_size
        N = offset.size(1) // 2

        if self.padding:
            x = self.zero_padding(x)

        # (b, 2N, h, w)
        p = self._get_p(offset, dtype)

        # (b, h, w, 2N)
        p = p.contiguous().permute(0, 2, 3, 1)
        q_lt = p.detach().floor()
        q_rb = q_lt + 1

        q_lt = torch.cat([torch.clamp(q_lt[..., :N], 0, x.size(2)-1), torch.clamp(q_lt[..., N:], 0, x.size(3)-1)], dim=-1).long()
        q_rb = torch.cat([torch.clamp(q_rb[..., :N], 0, x.size(2)-1), torch.clamp(q_rb[..., N:], 0, x.size(3)-1)], dim=-1).long()
        q_lb = torch.cat([q_lt[..., :N], q_rb[..., N:]], dim=-1)
        q_rt = torch.cat([q_rb[..., :N], q_lt[..., N:]], dim=-1)

        # clip p
        p = torch.cat([torch.clamp(p[..., :N], 0, x.size(2)-1), torch.clamp(p[..., N:], 0, x.size(3)-1)], dim=-1)

        # bilinear kernel (b, h, w, N)
        g_lt = (1 + (q_lt[..., :N].type_as(p) - p[..., :N])) * (1 + (q_lt[..., N:].type_as(p) - p[..., N:]))
        g_rb = (1 - (q_rb[..., :N].type_as(p) - p[..., :N])) * (1 - (q_rb[..., N:].type_as(p) - p[..., N:]))
        g_lb = (1 + (q_lb[..., :N].type_as(p) - p[..., :N])) * (1 - (q_lb[..., N:].type_as(p) - p[..., N:]))
        g_rt = (1 - (q_rt[..., :N].type_as(p) - p[..., :N])) * (1 + (q_rt[..., N:].type_as(p) - p[..., N:]))

        # (b, c, h, w, N)
        x_q_lt = self._get_x_q(x, q_lt, N)
        x_q_rb = self._get_x_q(x, q_rb, N)
        x_q_lb = self._get_x_q(x, q_lb, N)
        x_q_rt = self._get_x_q(x, q_rt, N)

        # (b, c, h, w, N)
        x_offset = g_lt.unsqueeze(dim=1) * x_q_lt + \\
                   g_rb.unsqueeze(dim=1) * x_q_rb + \\
                   g_lb.unsqueeze(dim=1) * x_q_lb + \\
                   g_rt.unsqueeze(dim=1) * x_q_rt

        # modulation
        if self.modulation:
            m = m.contiguous().permute(0, 2, 3, 1)
            m = m.unsqueeze(dim=1)
            m = torch.cat([m for _ in range(x_offset.size(1))], dim=1)
            x_offset *= m

        x_offset = self._reshape_x_offset(x_offset, ks)
        out = self.conv(x_offset)

        return out

    def _get_p_n(self, N, dtype):
        # 由于卷积核中心点位置是其尺寸的一半，于是中心点向左（上）方向移动尺寸的一半就得到起始点，向右（下）方向移动另一半就得到终止点
        p_n_x, p_n_y = torch.meshgrid(
            torch.arange(-(self.kernel_size-1)//2, (self.kernel_size-1)//2+1),
            torch.arange(-(self.kernel_size-1)//2, (self.kernel_size-1)//2+1))
        # (2N, 1)
        p_n = torch.cat([torch.flatten(p_n_x), torch.flatten(p_n_y)], 0)
        p_n = p_n.view(1, 2*N, 1, 1).type(dtype)

        return p_n

    def _get_p_0(self, h, w, N, dtype):
        # p0_y、p0_x就是输出特征图每点映射到输入特征图上的纵、横坐标值。
        p_0_x, p_0_y = torch.meshgrid(
            torch.arange(1, h*self.stride+1, self.stride),
            torch.arange(1, w*self.stride+1, self.stride))
        
        p_0_x = torch.flatten(p_0_x).view(1, 1, h, w).repeat(1, N, 1, 1)
        p_0_y = torch.flatten(p_0_y).view(1, 1, h, w).repeat(1, N, 1, 1)
        p_0 = torch.cat([p_0_x, p_0_y], 1).type(dtype)

        return p_0
    
    # 输出特征图上每点（对应卷积核中心）加上其对应卷积核每个位置的相对（横、纵）坐标后再加上自学习的（横、纵坐标）偏移量。
    # p0就是将输出特征图每点对应到卷积核中心，然后映射到输入特征图中的位置；
    # pn则是p0对应卷积核每个位置的相对坐标；
    def _get_p(self, offset, dtype):
        N, h, w = offset.size(1)//2, offset.size(2), offset.size(3)

        # (1, 2N, 1, 1)
        p_n = self._get_p_n(N, dtype)
        # (1, 2N, h, w)
        p_0 = self._get_p_0(h, w, N, dtype)
        p = p_0 + p_n + offset
        return p

    def _get_x_q(self, x, q, N):
        # 计算双线性插值点的4邻域点对应的权重
        b, h, w, _ = q.size()
        padded_w = x.size(3)
        c = x.size(1)
        # (b, c, h*w)
        x = x.contiguous().view(b, c, -1)

        # (b, h, w, N)
        index = q[..., :N]*padded_w + q[..., N:]  # offset_x*w + offset_y
        # (b, c, h*w*N)
        index = index.contiguous().unsqueeze(dim=1).expand(-1, c, -1, -1, -1).contiguous().view(b, c, -1)

        x_offset = x.gather(dim=-1, index=index).contiguous().view(b, c, h, w, N)

        return x_offset

    @staticmethod
    def _reshape_x_offset(x_offset, ks):
        b, c, h, w, N = x_offset.size()
        x_offset = torch.cat([x_offset[..., s:s+ks].contiguous().view(b, c, h, w*ks) for s in range(0, N, ks)], dim=-1)
        x_offset = x_offset.contiguous().view(b, c, h*ks, w*ks)

        return x_offset

参考：

更灵活、有个性的卷积——可变形卷积（Deformable Conv）

DeformableConv(可形变卷积)理论和代码分析 

仅为学习记录，侵删！ 

可变形卷积 deformable convolution 学习记录

Deformable ConvNets v1：
论文地址：https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch
工程地址：https://github.com/felixlaumon/deform-conv

论文地址： Deformable ConvNets v2: More Deformable, Better Results
工程地址：https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch

以下转摘于：https://blog.csdn.net/mykeylock/article/details/77746499
可变形卷积是指卷积核在每一个元素上额外增加了一个参数方向参数，这样卷积核就能在训练过程中扩展到很大的范围。
可变形卷积的论文为：Deformable Convolutional Networks【1】
而之前google一篇论文对这篇论文有指导意义：Spatial Transformer Networks【2】
论文【1】的github代码地址为https://github.com/felixlaumon/deform-conv
——————————————————————————————————————————
可变形卷积很好理解，但如何实现呢？实现方面需要关注两个限制：
1、如何将它变成单独的一个层，而不影响别的层；
2、在前向传播实现可变性卷积中，如何能有效地进行反向传播。
这两个问题的答案分别是：
1、在实际操作时，并不是真正地把卷积核进行扩展，而是对卷积前图片的像素重新整合，
变相地实现卷积核的扩张；
2、在图片像素整合时，需要对像素进行偏移操作，偏移量的生成会产生浮点数类型，
而偏移量又必须转换为整形，直接对偏移量取整的话无法进行反向传播，这时采用双线性差值的方式来得到对应的像素。
——————————————————————————————————————————
可变性卷积的流程为：
1、原始图片batch（大小为bhwc），记为U，经过一个普通卷积，卷积填充为same，即输出输入大小不变，
对应的输出结果为（bhw2c)，记为V，输出的结果是指原图片batch中每个像素的偏移量（x偏移与y偏移，因此为2c）。
2、将U中图片的像素索引值与V相加，得到偏移后的position（即在原始图片U中的坐标值），需要将position值限定为图片大小以内。
position的大小为（bhw*2c)，但position只是一个坐标值，而且还是float类型的，我们需要这些float类型的坐标值获取像素。
3、例，取一个坐标值（a,b)，将其转换为四个整数，floor(a), ceil(a), floor(b), ceil(b)，将这四个整数进行整合，
得到四对坐标（floor(a),floor(b)), ((floor(a),ceil(b)), ((ceil(a),floor(b)), ((ceil(a),ceil(b))。这四对坐标每个坐标都对应U
中的一个像素值，而我们需要得到(a,b)的像素值，这里采用双线性差值的方式计算
（一方面得到的像素准确，另一方面可以进行反向传播）。
4、在得到position的所有像素后，即得到了一个新图片M，将这个新图片M作为输入数据输入到别的层中，如普通卷积。
——————————————————————————————————————————

以上是可变性卷积的实现流程，但实际代码实现起来涉及到比较多的tensor操作，比较繁琐。
代码实现主要的文件有
cnn.py：采用keras定义了所有训练需要的层，可变形卷积层为ConvOffset2D，
layer.py：定义了ConvOffset2D可变形卷积类，主要包括keras中需要的call函数与init函数，
call函数首先调用普通卷积，然后调用deform_conv.py中函数实际计算。
deform_conv.py：真正实现可变形卷积计算的文件。
layer.py主要代码：

def __init__(self, filters, init_normal_stddev=0.01, **kwargs):
 
    self.filters = filters
    super(ConvOffset2D, self).__init__(
        self.filters * 2, (3, 3), padding='same', use_bias=False,
        kernel_initializer=RandomNormal(0, init_normal_stddev),
        **kwargs
    )
def call(self, x):
    """Return the deformed featured map"""
 
    #获取x大小，x大小为（b,h,w,c)，分别为batch_size,图片高度，图片宽度，特征图大小
 
    x_shape = x.get_shape()
 
    #调用普通卷积获得输出，输出结果为(b,h,w,2c)表示图片中每个像素需要偏移的量（x,y)
    offsets = super(ConvOffset2D, self).call(x)
     #reshape一下输出，方便后续操作，(b*c,h,w,2)表示共有b*c个图片，每个图片为h*w大小，每个像素对应2个方向
    # offsets: (b*c, h, w, 2)   
    offsets = self._to_bc_h_w_2(offsets, x_shape)
    #将原始输入也重新reshape一下方便后续操作
    # x: (b*c, h, w)
    x = self._to_bc_h_w(x, x_shape)
    #调用deform_conv.py中的函数根据原始图片与偏移量生成新图片数据。
    # X_offset: (b*c, h, w)
    x_offset = tf_batch_map_offsets(x, offsets)
    # x_offset: (b, h, w, c)
    x_offset = self._to_b_h_w_c(x_offset, x_shape)
    return x_offset
def compute_output_shape(self, input_shape):
    """Output shape is the same as input shape
    Because this layer does only the deformation part
    """
    return input_shape
@staticmethod
def _to_bc_h_w_2(x, x_shape):
    """(b, h, w, 2c) -> (b*c, h, w, 2)"""
    x = tf.transpose(x, [0, 3, 1, 2])
    x = tf.reshape(x, (-1, int(x_shape[1]), int(x_shape[2]), 2))
    return x
@staticmethod
def _to_bc_h_w(x, x_shape):
    """(b, h, w, c) -> (b*c, h, w)"""
    x = tf.transpose(x, [0, 3, 1, 2])
    x = tf.reshape(x, (-1, int(x_shape[1]), int(x_shape[2])))
    return x
@staticmethod
def _to_b_h_w_c(x, x_shape):
    """(b*c, h, w) -> (b, h, w, c)"""
    x = tf.reshape(
        x, (-1, int(x_shape[3]), int(x_shape[1]), int(x_shape[2]))
    )
    x = tf.transpose(x, [0, 2, 3, 1])
    return x

deform_conv.py主要代码：

def tf_flatten(a):
    """Flatten tensor"""
    return tf.reshape(a, [-1])
 
def tf_repeat(a, repeats, axis=0):
    """TensorFlow version of np.repeat for 1D"""
    # https://github.com/tensorflow/tensorflow/issues/8521
    assert len(a.get_shape()) == 1
    a = tf.expand_dims(a, -1)
    a = tf.tile(a, [1, repeats])
    a = tf_flatten(a)
    return a
def tf_repeat_2d(a, repeats):
    """Tensorflow version of np.repeat for 2D"""
    assert len(a.get_shape()) == 2
    a = tf.expand_dims(a, 0)
    a = tf.tile(a, [repeats, 1, 1])
    return a
def tf_map_coordinates(input, coords, order=1):
    """Tensorflow verion of scipy.ndimage.map_coordinates
    Note that coords is transposed and only 2D is supported
    Parameters
    ----------
    input : tf.Tensor. shape = (s, s)
    coords : tf.Tensor. shape = (n_points, 2)
    """
    assert order == 1
    coords_lt = tf.cast(tf.floor(coords), 'int32')
    coords_rb = tf.cast(tf.ceil(coords), 'int32')
    coords_lb = tf.stack([coords_lt[:, 0], coords_rb[:, 1]], axis=1)
    coords_rt = tf.stack([coords_rb[:, 0], coords_lt[:, 1]], axis=1)
 
    vals_lt = tf.gather_nd(input, coords_lt)
    vals_rb = tf.gather_nd(input, coords_rb)
    vals_lb = tf.gather_nd(input, coords_lb)
    vals_rt = tf.gather_nd(input, coords_rt)
 
 
    coords_offset_lt = coords - tf.cast(coords_lt, 'float32')
    vals_t = vals_lt + (vals_rt - vals_lt) * coords_offset_lt[:, 0]
    vals_b = vals_lb + (vals_rb - vals_lb) * coords_offset_lt[:, 0]
    mapped_vals = vals_t + (vals_b - vals_t) * coords_offset_lt[:, 1]
    return mapped_vals
def sp_batch_map_coordinates(inputs, coords):
    """Reference implementation for batch_map_coordinates"""
    coords = coords.clip(0, inputs.shape[1] - 1)
    mapped_vals = np.array([
        sp_map_coordinates(input, coord.T, mode='nearest', order=1)
        for input, coord in zip(inputs, coords)
    ])
    return mapped_vals
def tf_batch_map_coordinates(input, coords, order=1):
    """Batch version of tf_map_coordinates
    Only supports 2D feature maps
    Parameters
    ----------
    input : tf.Tensor. shape = (b, s, s)
    coords : tf.Tensor. shape = (b, n_points, 2)
    Returns
    -------
    tf.Tensor. shape = (b, s, s)
    """
    input_shape = tf.shape(input)
    batch_size = input_shape[0]
    input_size = input_shape[1]
    n_coords = tf.shape(coords)[1]
    coords = tf.clip_by_value(coords, 0, tf.cast(input_size, 'float32') - 1)
 
    #得到目标坐标左上角（left top）的整数坐标
    coords_lt = tf.cast(tf.floor(coords), 'int32')
 
    #得到又下角的整数坐标
    coords_rb = tf.cast(tf.ceil(coords), 'int32')
 
    #得到左下角的整数坐标
    coords_lb = tf.stack([coords_lt[..., 0], coords_rb[..., 1]], axis=-1)
 
    #得到右上角的整数坐标
    coords_rt = tf.stack([coords_rb[..., 0], coords_lt[..., 1]], axis=-1)
 
    #idx为索引展开，idx大小为（b*c*h*w)，形如(0,0,0,0,0,1,1,1,1,1,2,2,2,2,2,3,3,3,3,3)
 
    #b*c为5，h*w为4，总数为所有图片所有坐标总数
 
    idx = tf_repeat(tf.range(batch_size), n_coords)
    def _get_vals_by_coords(input, coords):
 
        #stack完后，每一个点表示一个坐标
 
        #形如
 
        #（0,0,0,0,0,1,1,1,1,1,2,2,2,2,2,3,3,3,3,3）
 
        # (3,2,1,2,3,1,2,3,0,0,0,3,2,1,1,2,3,2,0,0,2)
 
            # (3,2,1,0,0,2,0,3,1,2,3,0,0,2,3,0,1,2,0,2,3)
 
        indices = tf.stack([
            idx, tf_flatten(coords[..., 0]), tf_flatten(coords[..., 1])
        ], axis=-1)
        vals = tf.gather_nd(input, indices)
        vals = tf.reshape(vals, (batch_size, n_coords))
        return vals
     #以下为分别得到左上，左下，右上，右下四个点的像素值。
    vals_lt = _get_vals_by_coords(input, coords_lt)
    vals_rb = _get_vals_by_coords(input, coords_rb)
    vals_lb = _get_vals_by_coords(input, coords_lb)
    vals_rt = _get_vals_by_coords(input, coords_rt)
     #用双线性插值得到像素值。
    coords_offset_lt = coords - tf.cast(coords_lt, 'float32')
    vals_t = vals_lt + (vals_rt - vals_lt) * coords_offset_lt[..., 0]
    vals_b = vals_lb + (vals_rb - vals_lb) * coords_offset_lt[..., 0]
    mapped_vals = vals_t + (vals_b - vals_t) * coords_offset_lt[..., 1]
    return mapped_vals
def sp_batch_map_offsets(input, offsets):
    """Reference implementation for tf_batch_map_offsets"""
    batch_size = input.shape[0]
    input_size = input.shape[1]
    #生成grid，grid表示将一个图片的所有坐标变成两列，每一行两个元素表示x，y
 
    （grid的最后大小为(b*c,h*w,2)
    offsets = offsets.reshape(batch_size, -1, 2)
    grid = np.stack(np.mgrid[:input_size, :input_size], -1).reshape(-1, 2)
    grid = np.repeat([grid], batch_size, axis=0)
 
    #将原始坐标与坐标偏移量相加，得到目标坐标，coords的大小为(b*c,h*w,2)
    coords = offsets + grid
 
    #目标坐标需要在图片最大坐标范围内，将目标坐标进行切割限制
    coords = coords.clip(0, input_size - 1)
    #根据原始输入与目标坐标得到像素。
    mapped_vals = sp_batch_map_coordinates(input, coords)
    return mapped_vals
def tf_batch_map_offsets(input, offsets, order=1):
    """Batch map offsets into input
    Parameters
    ---------
    input : tf.Tensor. shape = (b, s, s)
    offsets: tf.Tensor. shape = (b, s, s, 2)
    Returns
    -------
    tf.Tensor. shape = (b, s, s)
    """
    input_shape = tf.shape(input)
    batch_size = input_shape[0]
    input_size = input_shape[1]
    offsets = tf.reshape(offsets, (batch_size, -1, 2))
    grid = tf.meshgrid(
        tf.range(input_size), tf.range(input_size), indexing='ij'
    )
    grid = tf.stack(grid, axis=-1)
    grid = tf.cast(grid, 'float32')
    grid = tf.reshape(grid, (-1, 2))
    grid = tf_repeat_2d(grid, batch_size)
    coords = offsets + grid
    mapped_vals = tf_batch_map_coordinates(input, coords)
    return mapped_vals