HDU 5895 Mathematician QSC(矩阵乘法+循环节降幂+除法取模小技巧+快速幂)——2016 ACM/ICPC Asia Regional Shenyang Online

Posted 2022-07-31 queuelovestack

此文章可以使用目录功能哟↑(点击上方[+])

 HDU 5895 Mathematician QSC

Accept: 0    Submit: 0
Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)

 Problem Description

QSC dream of becoming a mathematician, he believes that everything in this world has a mathematical law.

Through unremitting efforts, one day he finally found the QSC sequence, it is a very magical sequence, can be calculated by a series of calculations to predict the results of a course of a semester of a student.

This sequence is such like that, first of all,f(0)=0,f(1)=1,f(n)=f(n−2)+2∗f(n−1)(n≥2)Then the definition of the QSC sequence is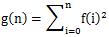. If we know the birthday of the student is n, the year at the beginning of the semester is y, the course number x and the course total score s, then the forecast mark is.

QSC sequence published caused a sensation, after a number of students to find out the results of the prediction is very accurate, the shortcoming is the complex calculation. As clever as you are, can you write a program to predict the mark?

 Input

First line is an integer T(1≤T≤1000).

The next T lines were given n, y, x, s, respectively.

n、x is 8 bits decimal integer, for example, 00001234.

y is 4 bits decimal integer, for example, 1234.

n、x、y are not negetive.

1≤s≤100000000

 Output

For each test case the output is only one integer number ans in a line.

 Sample Input

2
20160830 2016 12345678 666
20101010 2014 03030303 333

 Sample Output

1
317

 Problem Idea

解题思路:

【题意】
已知f(0)=0,f(1)=1,f(n)=f(n−2)+2∗f(n−1)(n≥2)

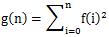
给你n,y,x,s的值

求的值

【类型】
矩阵乘法+循环节降幂+除法取模小技巧+快速幂
【分析】
一开始想简单了,对于a^x mod p这种形式的直接用欧拉定理的数论定理降幂了

结果可想而知,肯定错,因为题目并没有保证gcd(x,s+1)=1,而欧拉定理的数论定理是明确规定的

所以得另谋出路

那么网上提供了一种指数循环节降幂的方法

具体证明可以自行从网上找一找

有了这种降幂的方法之后,我们要分析一下如何求g(n)

由于f(0)=0,f(1)=1,f(n)=f(n−2)+2∗f(n−1)(n≥2)

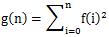
∴f(0)=0,f(1)=1,f(2)=2,f(3)=5,f(4)=12,f(5)=29,f(6)=70……

∴g(0)=f(0)*f(0)=0=f(0)*f(1)/2

  g(1)=g(0)+f(1)*f(1)=1=f(1)*f(2)/2

  g(2)=g(1)+f(2)*f(2)=5=f(2)*f(3)/2

  g(3)=g(2)+f(3)*f(3)=30=f(3)*f(4)/2

  g(4)=g(3)+f(4)*f(4)=174=f(4)*f(5)/2

  g(5)=g(4)+f(5)*f(5)=1015=f(5)*f(6)/2

  ……

可得,g(n)=f(n)*f(n+1)/2

这个是很好发现的

如果你发现不了的话,可以直接丢到OEIS里搜一下

然后,要求出g(n*y),就需要先求出f(n*y)和f(n*y+1)

这时,我们可以考虑用矩阵乘法

构造矩阵

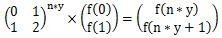
套一下矩阵快速幂的模板就可以求出f(n*y)和f(n*y+1)

然后要求g(n)还有个除以2的操作,显然除法取模要用逆元

但考虑到2与模数不一定互质,无法用乘法逆元,所以要采用一点小技巧转化一下

这样我们就可以得到简化好的最终的指数部分

这样我们用快速幂就可以求x的幂次对(s+1)取模了

【时间复杂度&&优化】
O(1ogn)

题目链接→HDU 5895 Mathematician QSC

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 2;
const int M = 100005;
const int inf = 1000000007;
//const int mod = 1000000007;
typedef struct node

    __int64 a[N][N];
    void Init()
    
        memset(a,0,sizeof(a));
        for(int i=0;i<N;i++)
            a[i][i]=1;
    
matrix;
int mod;
bool flag;
matrix mul(matrix a,matrix b)//矩阵乘法

    matrix ans;
    for(int i=0;i<N;i++)
        for(int j=0;j<N;j++)
        
            ans.a[i][j]=0;
            for(int k=0;k<N;k++)
            
                ans.a[i][j]+=a.a[i][k]*b.a[k][j];
                if(ans.a[i][j]>mod)
                    ans.a[i][j]=ans.a[i][j]%mod+mod;
            
        
    return ans;

matrix pow(matrix a,__int64 n)//求a^n

    matrix ans;
    ans.Init();
    while(n)
    
        if(n%2)
            ans=mul(ans,a);
        
        n/=2;
        a=mul(a,a);
    
    return ans;

int euler(int n)

    int ans=1,i;
    for(i=2;i*i<=n;i++)
    
        if(n%i==0)
        
            n/=i;
            ans*=i-1;
            while(n%i==0)
            
                n/=i;
                ans*=i;
            
        
    
    if(n>1)
        ans*=n-1;
    return ans;

__int64 Quick_Mod(__int64 a, __int64 b, __int64 m)

    __int64 res = 1,term = a % m;
    while(b)
    
        if(b & 1) res = (res * term) % m;
        term = (term * term) % m;
        b >>= 1;
    
    return res%m;

int main()

    int t,n,y,x,s;
    __int64 z;
    matrix ans,k;
    scanf("%d",&t);
    while(t--)
    
        k.a[0][0]=0;k.a[0][1]=1;
        k.a[1][0]=1;k.a[1][1]=2;
        ans.a[0][0]=0;ans.a[0][1]=0;
        ans.a[1][0]=1;ans.a[1][1]=0;
        scanf("%d%d%d%d",&n,&y,&x,&s);
        mod=2*euler(s+1);
        z=n;z*=y;
        ans=mul(pow(k,z),ans);
        z=(ans.a[0][0]*ans.a[1][0])%mod+mod;
        z=(z%mod+mod)/2;
        printf("%I64d\\n",Quick_Mod(x,z,s+1));
    
    return 0;

菜鸟成长记