标量向量矩阵微积分

Posted 2022-07-20 _less is more

首先引入三个重要概念
1、分子布局（Numerator-layout notation）
2、分母布局（Denominator-layout notation）
3、混合布局（Mixed layout）

接下来我们会对这三个概念进行深入了解。

一、布局公约

当我们在探究机器学习、深度学习时，时常会遇到标量与向量，向量与矩阵等之间的微分，求其导数或梯度。但我们需要知道，不同的作者或上课的教授会使用不同的布局对导数的结果进行表示，所以我们经常会看到不同源的导数和梯度看起来大致相同，但维度总是不一致，那是因为他们用了不同的布局；再者，即便同一个作者，对不同类型的公式进行描述时，为了方便，可能也会使用不同的布局来进行表示，因此我们需要非常小心地理解其背后的表示方法，才不会被困扰。

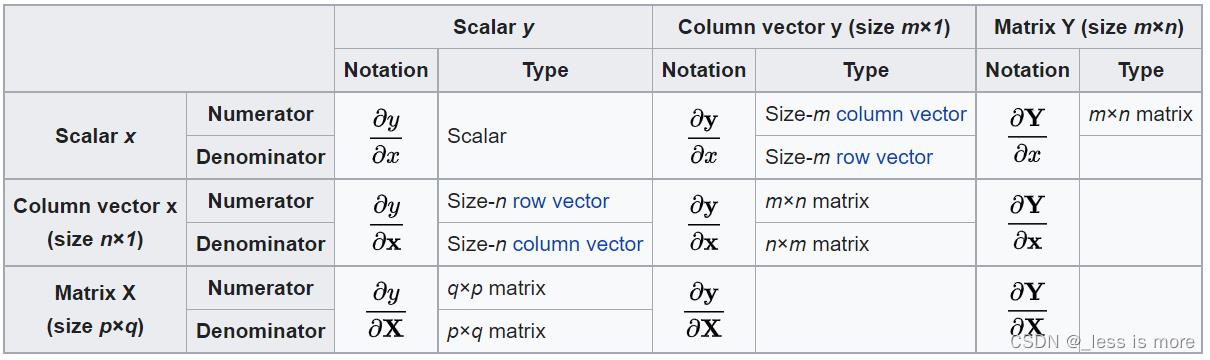
二、向量对向量求导，结果为矩阵

以$\frac{\partial y}{\partial x}$为例（都是向量）

简而言之，
分子布局以$y$和$x^T$来表示结果。
分母布局以$y^T$和$x$来表示结果。
混合布局和分子布局一样，同样以$y$和$x^T$来表示结果，但不同的是它会把$x^T$直接表示在$\frac{\partial y}{\partial x}$上，变成$\frac{\partial y}{\partial x^T}$

举例：
如果$y$是m维度的列向量，维度表示为（m，1）；$x$是n维度的列向量，表示为（n，1）。

按照分子布局，$y$仍然是（m，1），纵向排开，而$x^T$变成（1，n），横向排开，则$\frac{\partial y}{\partial x}$最终维度为（m，n），m为纵向维度，n为横向维度。

按照分母布局，$y^T$变成（1，m），横向排开，而$x$仍然是（n，1），纵向排开，则$\frac{\partial y}{\partial x}$最终维度为（n，m），n为纵向维度，m为横向维度。

按照混合布局，最终结果仍然是（m，n）维度。

三、其他资料

图片来源

如下是按分子布局来计算维度

图片来源