极智AI | 详解 遗传算法 实现

Posted 2022-07-15 极智视界

  欢迎关注我的公众号 [极智视界]，获取我的更多笔记分享

  大家好，我是极智视界，本文详细介绍一下 遗传算法的原理和实现。

  遗传算法（Genetic Algorithm, GA）起源于对生物系统所进行的计算机模拟研究，它是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，借鉴了达尔文的进化论和孟德尔的遗传学说，遵循自然界 “适者生存、优胜劣汰” 的原则。

文章目录

• • 1 遗传算法的主要步骤
  • 2 袋鼠跳例子

1 遗传算法的主要步骤

1. encode: 将问题的候选解用染色体表示，实现解空间向编码空间的映射过程,编码方式有很多，如二进制编码、实数向量编码、整数排列编码、通用数据结构编码等等。通常使用二进制编码，用 0 和 1 组成的数字串模拟染色体，可以很方便地实现基因交叉、变异等操作；

2. 种群初始化：产生代表问题可能潜在解集的一个初始群体（编码集合），从群体多样性方面考虑，群体越大越好，避免陷入局部最优；从计算效率方面考虑，群体规模越大将导致计算量的增加；

3. 计算个体适应度： 适应度函数（Fitness Function）的选取直接影响到遗传算法的收敛速度以及能否找到最优解，因为在进化搜索中基本不利用外部信息，仅以适应度函数为依据，利用种群每个个体的适应程度来指导搜索；

4. 进化计算：通过选择、交叉、变异，产生出代表新的解集的群体。选择（selection）：根据个体适应度大小，按照优胜劣汰的原则，淘汰不合理的个体；交叉（crossover）：编码的交叉重组，类似于染色体的交叉重组；变异（mutation）：编码按小概率扰动产生的变化，类似于基因突变；

5. decode： 最优解还是一个由 0 和 1 组成的数字串，要将它转换成十进制才能供我们理解和使用;

2 袋鼠跳例子

  一元函数：f(x) = x*sin(10*pi*x)+2, -1<x<2，目标是找到 最大值，这个函数图示意如下：

  这里假设每个解都是个袋鼠，我们希望它们不断的向着更高处跳去，直到跳到最高的山峰（尽管袋鼠本身不见得愿意那么做）。所以求最大值的过程就转化成一个 “袋鼠跳” 的过程。换个说法。从前，有一大群袋鼠，它们被莫名其妙的零散地遗弃于喜马拉雅山脉。于是只好在那里艰苦的生活。海拔低的地方弥漫着一种无色无味的毒气，海拔越高毒气越稀薄。可是可怜的袋鼠们对此全然不觉，还是习惯于活蹦乱跳。于是，不断有袋鼠死于海拔较低的地方，而越是在海拔高的袋鼠越是能活得更久，也越有机会生儿育女。就这样经过许多年，这些袋鼠们竟然都不自觉地聚拢到了一个个的山峰上，这样就能找到最优解。

  用 matlab 实现：

function main()
clear;
clc;
%种群大小
popsize = 100;
%二进制编码长度
chromlength = 10;
%交叉概率
pc = 0.6;
%变异概率
pm = 0.001;
%初始种群，随机生成二进制数字
pop=initpop(popsize, chromlength);
for i = 1:100
	%计算适应度值 (函数值)
	objvalue = cal_objvalue(pop);
	fitvalue = objvalue;
	%选择操作
	newpop = selection(pop, fitvalue);
	%交叉操作
	newpop = crossover(newpop, pc);
	%变异操作
	newpop = mutation(newpop, pm);
	%更新种群
	pop = newpop;
	%寻找最优解
	[bestindividual, bestfit] = best(pop, fitvalue);
	x2 = binary2decimal(bestindividual);
	x1 = binary2decimal(newpop);
	y1 = cal_objvalue(newpop);
	if mod(i, 10) == 0
		figure;
		fplot('xsin(10pix)+2', [0 10]);
		hold on;
		plot(x1, y1, '*');
		title(['迭代次数为 n=' num2str(i)]);
		%plot(x1, y1, '*');
	end
end
fprintf('The best X is --->>%5.2f\\n', x2);
fprintf('The best Y is --->>%5.2f\\n', bestfit);

%适应性函数
function [objvalue] = cal_objvalue(pop);
x = binary2decimal(pop);
%转换二进制数为 x 变量的变化域范围的数值，这里适应性函数 (fitness function) 的衡量标准就是 f(x) 即海拔高度
objvalue = xsin(10pix)+2

  自然界中，越适应的个体就越有可能繁殖后代。但是也不能说适应度越高的就肯定后代越多，只能是从概率上来说更多.代码中用轮盘赌（Roulette Wheel Selection）选择法。比如我们有 5 条染色体，他们所对应的适应度评分分别为：5，7，10，13，15。总的适应度为：

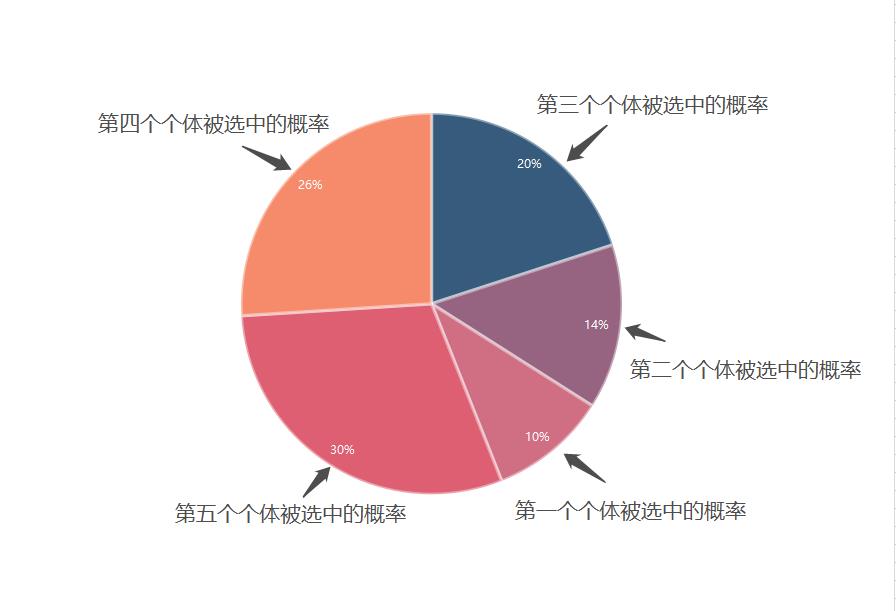
  所以适应度高被选中的几率越高:

function [newpop] = selection(pop, fitvalue)
%构造轮盘
[px, py] = size(pop);
totalfit = sum(fitvalue);
p_fitvalue = fitvalue / totalfit;
%概率求和排序
p_fitvalue = cumsum(p_fitvalue);
%从小到大排列
ms = sort(rand(px, 1));
fitin = 1;
newin = 1;
while newin <= px
	if(ms(newin)) < p_fitvalue(fitin)
		newpop(newin, :) = pop(fitin, :);
		newin = newin + 1;
	else
		fitin = fitin + 1;
	end
end

  接着进行基因交叉，即随机把其中几个位于同一位置的编码进行交换，产生新的个体：

%基因交叉
function [newpop]  = crossover(pop, pc)
[px, py] = size(pop);
newpop = ones(size(pop));
for i = 1:2:px-1
	if(rand < pc)
		cpoint = round(rand * py)
		newpop(i, :) = [pop(i, 1:cpoint), pop(i+1, cpoint+1:py)];
		newpop(i+1, :) = [pop(i+1, 1:cpoint), pop(i, cpoint+1:py)];
	else
		newpop(i, :) = pop(i, :);
		newpop(i+1, :) = pop(i+1, :);
	end
end

  然后进行基因变异，即染色体的某一个位点上基因的改变，基因串上的 “ 0” 或 “ 1” 有一定几率变成与之相反的 “ 1” 或 “ 0”：

%基因变异
function [newpop] = mutation(pop, pm)
[px, py] = size(pop);
newpop = ones(size(pop));
for i = 1:px
	if(rand < pm)
		mpoint = round(rand * py);
		if mpoint <= 0
			mpoint = 1;
		end
		newpop(i, :) = pop(i, :);
		if newpop(i, mpoint) == 0
			newpop(i, mpoint) = 1;
		else newpop(i, mpoint) == 1
			newpop(i, mpoint) = 0;
		end
	else newpop(i, :) = pop(i, :);
	end
end

  最后选择最优个体：

%求最优适应度函数
function [bestindividual, bestfit] = best(pop, fitvalue)
[px, py] = size(pop);
bestindividual = pop(1, :);
bestfit = fitvalue(1);
for i = 2:px
	if fitvalue(i) > bestfit
		bestindividual = pop(i, :);
		bestfit = fitvalue(i);
	end
end

  来看结果，迭代数 gn = 1：

  迭代数 gn = 10：

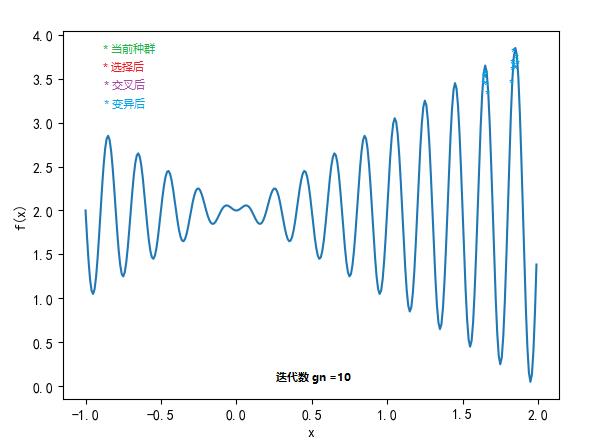
  可以看到袋鼠跳的趋势是在往上 -> 最后都在往顶峰跳，效果还可以。

  好了，以上分享了 详解 遗传算法 实现。希望我的分享能对你的学习有一点帮助。

 【公众号传送】

《极智AI | 详解 遗传算法 实现》

扫描下方二维码即可关注我的微信公众号【极智视界】，获取我的更多经验分享，让我们用极致+极客的心态来迎接AI ！