LeetCode 0110.平衡二叉树 - 自底向上

Posted 2022-07-13 Tisfy

【LetMeFly】110.平衡二叉树 - 自底向上

力扣题目链接：https://leetcode.cn/problems/balanced-binary-tree/

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

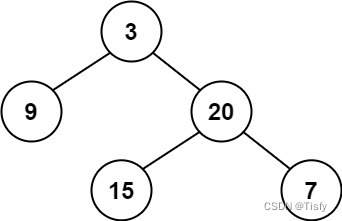
输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

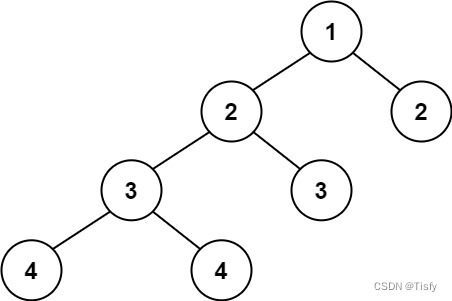
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

提示：

• 树中的节点数在范围 [0, 5000] 内
• -104 <= Node.val <= 104

方法一：110.平衡二叉树 - 自底向上

判断一棵树是否为平衡二叉树，只需要判断左子树的和右子树的高度之差的绝对值是否 ≤ 1

我们只需要求出每个节点为根的树的高度（$\max (左子树,右子树)+1$），并且在求高度的过程中，判断左右子树的高度差是否大于1即可（若大于1，则记录下来）。

bool ok = true;

int getHeight(TreeNode* root) 
	if (!root)  // 空节点高度为0
		return 0;
	int left = getHeight(root->left);  // 左子树的高度
	int right = getHeight(root->right);  // 右子树的高度
	if (abs(left - right) > 1)   // 高度差大于1
		ok = false;  // 则不是平衡二叉树
	
	return max(left, right) + 1;  // 以root为根的树的高度是max(left, right) + 1

因为递归过程中，其实是先求的叶节点的高度，因此美其名曰自底向上

• 时间复杂度$O(n)$，其中$n$是二叉树节点的个数（每个节点只需要遍历一次）
• 空间复杂度$O(n)$，空间复杂度的消耗主要来自递归

AC代码

C++

class Solution 
private:
    bool ok = true;

    int getHeight(TreeNode* root) 
        if (!root)
            return 0;
        int left = getHeight(root->left);
        int right = getHeight(root->right);
        if (abs(left - right) > 1) 
            ok = false;
        
        return max(left, right) + 1;
    
public:
    bool isBalanced(TreeNode* root) 
        getHeight(root);
        return ok;
    
;

同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/125691684