数学知识复习：第二型曲线积分

Posted 2022-07-01 UQI-LIUWJ

0 引出

        设一质点在力F的作用下，沿曲线C运动，力F在曲线C的各点处的方向和大小可以是不同的，F(x,y)是一个向量函数，那么如何计算这个质点在变力F的作用下，沿曲线C由点A运动到点B所做的功呢？

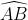          弧上从A到B依次取点，于是 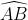被分割成n段小弧 .

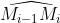        我们先考虑力F沿着小弧运动所做的功。在小弧上任取一点，以处的力F作为 小弧 上各点的力。同时近似地认为 小弧 是直线段。

        我们以内积 F ·作为力F沿着小弧运动所做的功的近似式。

        所以和式是所求功W的近似值。

         如果F(x,y)=P(x,y)i+Q(x,y)j, ,那么 ，其中

         所以

 1 定义

 

 2 性质

（1）F，G在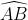 上连续，a,b是常数，则有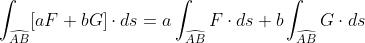

（2）如果曲线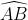 上一点C将积分路线 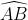 分成两段,,则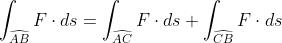

（3）

 

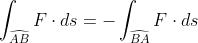
 3 计算方法

也是转化成定积分

如果曲线C的参数方程是，当参数t从α变到β时，点(x,y)从A变到B（此时不一定α比β小！）；同时在α和β之间连续，F在上连续（即P,Q在上连续）

则第二型曲线积分 可以转化为

如果弧的方程为y=y(x)，其中x从α变化到β，那么有：

 

 如果弧的方程为x=x(y)，其中y从c变化到d，那么有：

  

 4 第一型曲线积分和第二型曲线积分的关系