什么是无偏估计和有偏估计

Posted 2023-03-28

参考技术A

有偏估计（biased estimate）是指由样本值求得的估计值与待估参数的真值之间有系统误差，其期望值不是待估参数的真值。

无偏估计是用样本统计量来估计总体参数时的一种无偏推断。估计量的数学期望等于被估计参数的真实值，则称此估计量为被估计参数的无偏估计，即具有无偏性，是一种用于评价估计量优良性的准则。

假设A市有10000名小学六年级的学生，他们进行一次考试，成绩服从1～100的均匀分布。1号学生考1分，2号学生考1.01分......10000号学生考100分。

那么，他们的平均分为(1+1.01+1.02+...+100)/10000=50.5，这个值是总体期望，但实际上我们并不能知道这个值，只能通过样本估计。

可以给A市88所小学打电话，让学校老师随机选取一名学生成绩报上来，这样就可以得到88名学生的成绩，这88名学生就是我们第一个随机选取的样本，我们算出平均值，记作。

然后再重新给A市88所小学打电话，重新随机选取88名学生的成绩，这是第二个随机样本。算出样本2的平均值，记作。

然后重复n遍，获得n个样本均值，你会发现样本均值的分布符合正态分布。我们就可以用最大似然估计或距估计求得这个正态分布的期望。

而样本平均数的期望（在这里就是均值），极其接近总体的期望。我们称之为无偏估计，一次抽样计算的平均值就说是总体均值的做法就是有偏估计（biased estimator）

扩展资料

(1)无偏估计有时并不一定存在。

(2)可估参数的无偏估计往往不唯一。统计学中，将存在无偏估计的参数称为可估参数，可估参数的无偏估计往往不唯一，而且只要不唯一，则即有无穷多个。一个参数往往有不止一个无偏估计。

(3)无偏估计不一定是好估计。

参考资料来源：百度百科-有偏估计

参考资料来源：百度百科-无偏估计

方差的无偏估计如何计算？

　　我们常常被问到"方差的无偏估计如何计算？和有偏估计的区别是什么？"，心想"哎呀，又忘了"。本篇回归问题本质，带你理解这些名词背后解决的实际问题。

一、基本概念

　　解题第一步是理解题意，通过示例首先搞清楚以下几个概念。

　　假如你想调研所在大学女生的身高，你站在厕所门口（女生一般爱上厕所^~^），随机去问n个女生（独立同分布），最后通过哪些数值来反映身高呢？一般我们都会使用均值。

　　但如果在调研的时候，你发现有的女生特别高（猜测是校篮球队的），该样本并不能真实反映女生普遍身高，这就导致采集的样本存在异常数据，那么你可以通过方差来度量身高的差异。

　　由于学校的全体女生身高的均值µ 和方差σ² 未知，这里通过采样计算得到的和 S²，都只是对已知分布中的未知参数的一个估计，这就是估计量。在估计时用到的样本均值和样本方差是用来描述数据特征的，被叫做是统计量。

　　上面示例提到以下概念，严格定义如下：

• 期望

  是指随机事件中随机变量和它出现概率的乘积的总和，反映了随机变量平均取值的大小，又称"均值"。

  E(X) = Σ_ip(x_i)x_i

• 方差

  是用来度量随机变量和其均值之间的偏离程度，方差越小，偏离程度越小。

  D(X) = E([X-E(X)]²)

• 统计量

  已知样本集，由样本值计算的函数，被称为统计量，不含未知参数。比如样本平均值，样本方差，样本标准差等。

• 估计量

  设总体样本的分布函数已知，参数未知。已知样本集，需要构造适当的统计量来估计未知参数的近似值，这被称为估计量。

二、那么问题来了

　　以上示例中两个指标的计算方式如下：

　　样本均值

             

　　样本方差

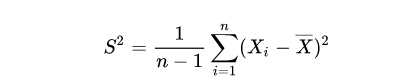
　　为什么方差的计算分母是n-1，而不是n ？

　　实际上示例中的统计量是对未知参数的估计，而估计量的选择是有评价标准的，以下是三种常见的评价指标，这里只考察估计量的无偏性。

三、估计量的评价标准

　　1. 无偏性

　　若估计量的数学期望存在，且期望等于未知参数，则称该估计量为参数的无偏估计量。

　　估计量的无偏性是指对于某些样本值来说，得到的估计量和真值相比，有的偏大，有的偏小，但就其平均而言，偏差为0。估计量的期望和真值相差被称为系统误差，无偏估计实际上是指无系统误差。

　　2. 有效性

　　设有两个无偏估计量，都是真值的估计，其中方差小的估计量较方差大的更有效。

　　估计量的有效性，是希望无偏估计量取值偏离真值的程度越小越好，所以以方差小的估计量更好。

　　3. 相合性

　　随着样本数无限增加，估计量依概率收敛于真值，则被称为相合估计量。

　　以上两个标准都是以样本数固定为前提，我们希望随着样本的增加，估计量的值趋近于参数的真值。 

四、方差的无偏性

　　由以上无偏性标准的定义可知，方差的无偏估计需要估计量的均值等于方差真值，当分母是n时，如下公式可见

　　1. 公式推导

   　   

                

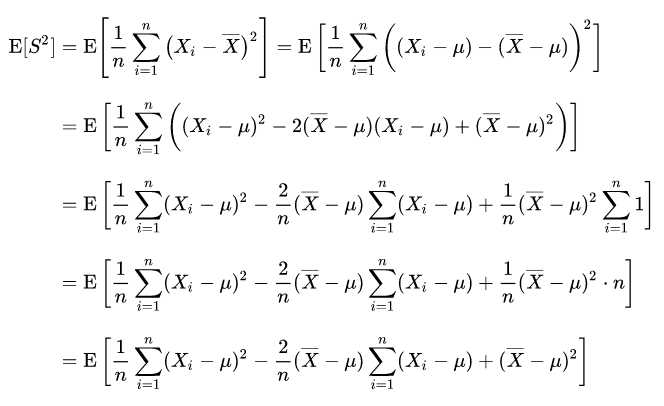
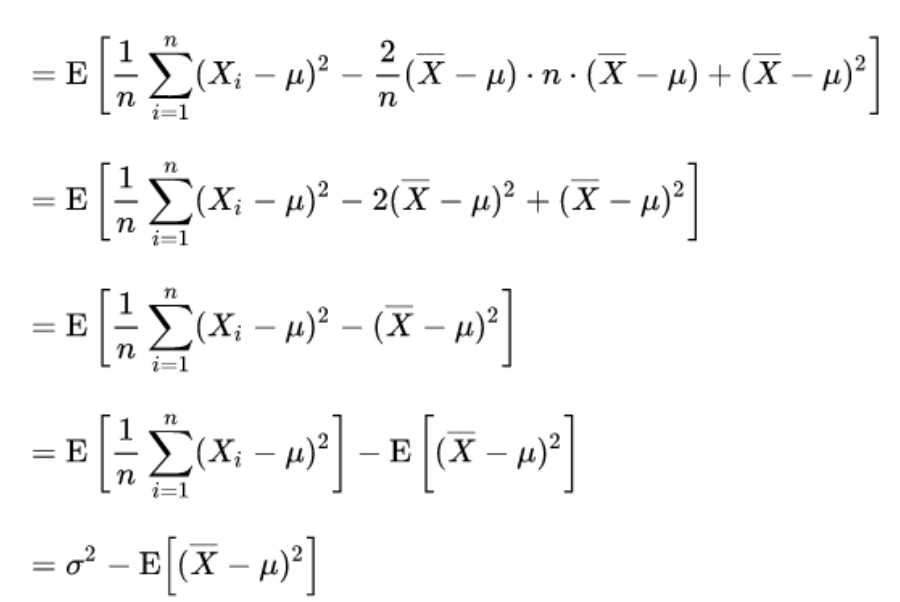
　　又由于

      

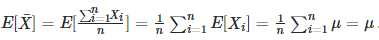
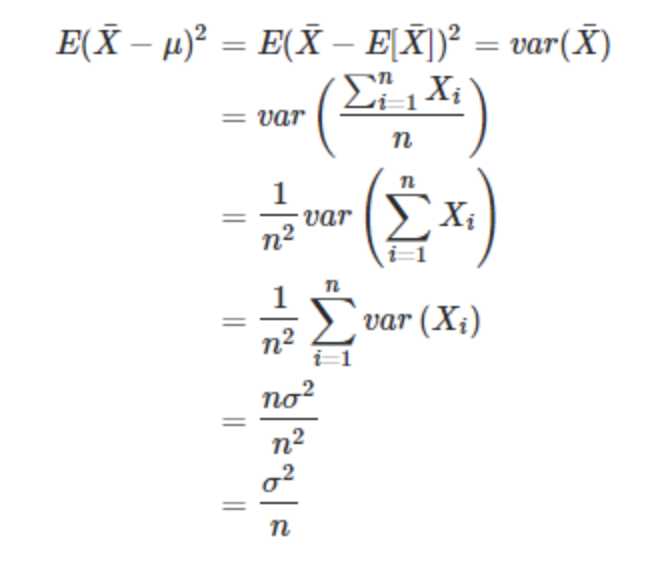
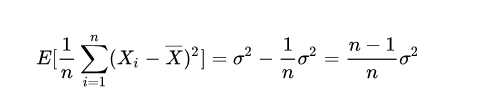
　　即：

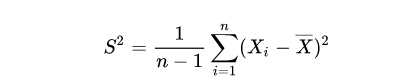
　　2.通俗理解（自由度）

　　计算估计量的样本需要独立同分布，由于分布参数未知，使用样本均值来计算样本方差时，样本均值是由各样本计算而来。假设样本容量为n，已知n-1个样本值，可由样本均值推断出最后一个样本取值，破坏了样本独立性，故该样本集的自由度为n-1，所以计算样本方差时样本数应该减去1。

 

 

参考：

https://www.zhihu.com/question/20099757

《概率论与数理统计》