综合评价方法之秩和比法（RSR）

Posted 2022-06-29 卖山楂啦prss

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了综合评价方法之秩和比法（RSR）相关的知识，希望对你有一定的参考价值。

一、概念

秩和比法是一种将古典参数统计和近代非参数统计进结合，并融其各自优点于一身的统计分析方法，1988年由田风调教授提出，适合对行列表格的资料进行综合评价，也可应用于分类及计量资料的综合评价。

秩和比（RSR）指在多指标综合评价中，表中各评价对象 n 秩次的相对平均值（若评价指标权重不同，则需要指标乘以权重），是一个非参数计量，具有0-1区间连续变量的特征。

其基本思想是在一个 n 行（n 评价对象）p 列（p 个评价指标）矩阵中，通过秩转换，获得无量纲的统计量RSR，以RSR值对评价对象的优劣进行排序或分档排序。

在综合评价中，秩和比的值能够包含所有评价指标的信息，显示出这些评价指标的综合水平，RSR值越大表明综合评价越优。

优点：因为 RSR 只使用了数据的相对大小关系，而不真正运用数值本身，所以此方法综合性强，可以显示微小变动，对离群值不敏感；能够对各个评价对象进行排序分档，找出优劣，是做比较，找关系的有效手段；能够找出评价指标是否有独立性。
缺点：通过秩替代原始指标值，会损失部分信息；不容易对各个指标进行恰当的编秩。

二、步骤

Step1：列出原始数据，一行代表一个评价对象，一列代表一个评价指标。
Step2：由原始数据进行计算秩值；
Step3：利用Step2的秩值，计算得到RSR值和RSR值排名；
Step4：列出RSR的分布表格情况并且得到Probit值；
Step5：计算回归方程；
Step6：进行排序，并且进行分档等级。

（1）列出原始数据表

根据评价的目的，选择适当的评价指标。使用专业知识区分指标是高优还是低优。一般高优指标是指效益型指标，即指标的数值越大越理想；低优指标就是成本型指标，即指标的数值越小越理想

有时，指标的属性要根据不同的研究目的加以确定，还有一些指标为不分高优与低优的指标。

列出原始数据表。假设有n个待评价样本，p项评价指标，形成原始指标数据矩阵：
$X=\\left( \\beginmatrix x_11& ...& x_1p\\\\ \\vdots& \\ddots& \\vdots\\\\ x_n1& \\cdots& x_np\\\\ \\endmatrix \\right)$

其中 $X_ij$ 表示第 i 个样本第 j 项评价指标的数值。

例如：

	GDP	就业人数	财政支出	人均可支配收入
北京	xx	xx	xx	xx
上海	xx	xx	xx	xx
广州	xx	xx	xx	xx
深圳	xx	xx	xx	xx
成都	xx	xx	xx	xx
重庆	xx	xx	xx	xx
天津	xx	xx	xx	xx

（2）计算秩值

根据每一个具体的评价指标按其指标值的大小进行排序，得到秩次R，用秩次R来代替原来的评价指标值。

根据编秩结果建立各指标的秩次数据矩阵。
$R=\\left( \\beginmatrix R_11& R_12& \\cdots& R_1p\\\\ R_21& R_22& \\cdots& R_2p\\\\ \\vdots& \\vdots& & \\vdots\\\\ R_n1& R_n2& \\cdots& R_np\\\\ \\endmatrix \\right)$

$R_ij$ ：表示第 i 个样本第 j 项评价指标的秩次。

这里的秩可以理解成是一种顺序或者排序，它是根据原始数据的排序位置进行求解

例如：
高优指标j  [-0.8，1.1，-2，4.2，-3.1]

排序

[-3.1，-2，-0.8，1.1，4.2]

秩 3  4  2 5 1

编出每个指标各对象的秩，这是秩和比法运用成败的关键之一。编秩时，应充分体现专业要求，力求所编秩次无逻辑上的混乱。

编制方法：

共有两种方法，分别是整次法和非整次法；二者在于计算秩的时候公式不一样

整秩法

高优指标从小到大编秩，低优指标从大到小编秩，同一指标数据相同者取平均值。

非整秩法

对于高优指标： $R_ij=1+\\left( n-1 \\right) \\fracX_ij-X_\\minX_\\max-X_\\min$
对于低优指标：
$R_ij=1+\\left( n-1 \\right) \\fracX_\\max-X_ijX_\\max-X_\\min$

其中 $X_\\max=\\max \\left( X_1j,X_2j,\\cdots ,X_nj \\right) \\text，X_\\min=\\min \\left( X_1j,X_2j,\\cdots ,X_nj \\right)$

一般使用整秩法

例如

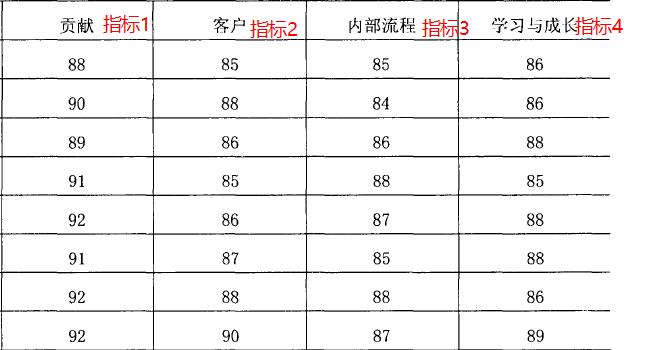
均是高优指标，按从小到大编秩

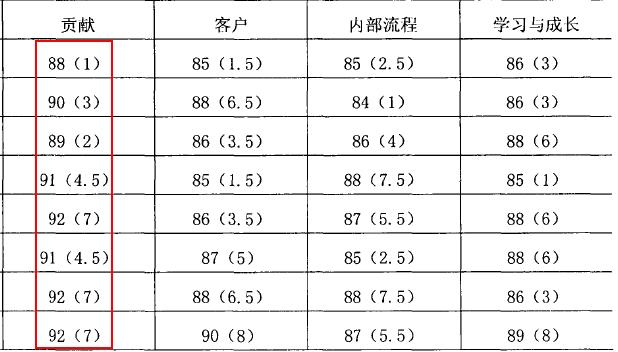
（3）计算秩和比RSR值及排名

在一个 n 行（ n 个评价对象）p 列（ p 个评价指标）矩阵中，RSR的计算公式为：
$RSR_i=\\frac1n\\times p\\sum_j=1^pR_ij$

上式中， $i=1,2,\\cdots ,n\\ \\text；\\ j=1,2,\\cdots ,p$