白话空间统计之：空间自相关

Posted 2022-06-21 虾神说D

白话空间统计之：空间自相关

空间自相关，肯定是空间统计里面第一个拦路虎了，很多人遇上了这个高大上的词汇，立刻就发现，这五个字我好像都认识，但是到底说了啥？不知道。

如果翻开各种教材，从统计学到数学到物理学，各种解释都摆出了一副“老子就是高大上学霸，屌丝学渣勿扰”的样子，这个东西真得就那么难么？虾神我就不信了，所以：I have a dream，就是写出一个最接地气的空间统计解释来。（好大的宏愿，阿弥陀佛老天保佑，别吹炸了。）

首先，要明白一下空间自相关这个神奇的概念，不得不先说一个神奇的人物。他就是号称“近代地理学界的牛顿”的Waldo Tobler（金都 托布勒）教授。

Waldo教授1930年生于瑞士，1961年在美国华盛顿大学获得博士学位，这一年也是风起云涌的一年，当今美利坚大统领奥巴马同学就是1961年出生的。

似乎是老天爷见物理已经有了三大定律，而地理学一个也没有，于是在1969年（也有说1970年）的时候，上帝一挥手，让Waldo教授照亮地理学的天空吧。所以那一年，他发表了史称“地理学第一定律”的“Tobler’s First Law”（简称TFL），即为“all attribute values on a geographic surface are related to each other, but closer values are more strongly related than are more distant ones”翻译成大白话，就是：任何事情呢，都是有关系，只不过靠得越近，关系就越紧密。

正如牛顿的三大定律开创了经典力学体系，地理学的第一定律也为计量革命提供了理论基础，从此，空间分析和空间统计领域再也离不开这个定律了。

正如明代学者茅无仪评价孙子兵法“前孙子者,孙子不遗;后孙子者,不能遗孙子”，TFL也在地理学界做到了前者不遗，后者不能遗的境界。

依照定律，空间中的每一个事务，都是有联系的，近的事务之间的联系紧密程度，要高于距离远的事务之间的联系程度。所谓的联系紧密程度，自然也可以说，两个事务会在某一方面，有相似的地方。

那么空间自相关这个概念就被带出来了。

什么是空间自相关呢？首先我们来看看下面一个例子：

时间：课间操。

地点：学校操场。

当广播响起来的时候，所有学生都一路狂奔冲向操场（迟到要挨罚的），所以，校长在楼上，看见的应该是这样的一个场面：

怎是一个乱字了得，那么这就是所谓的“随机分布”，谁也不知道，哪个学生是哪个班的。

随着体育老师的口令，慢慢得变成了下面这个场面：

学生整整齐齐的占成了队列，每个人前后左右的距离都是一样，这个就是所谓的“均匀分布”，在这种均匀分布的情况下，照样没办法看出学生之间的关系。

5分钟后，广播体操结束，同样随着体育老师的一声口令，解散，学生们就变成了下面这个样子：

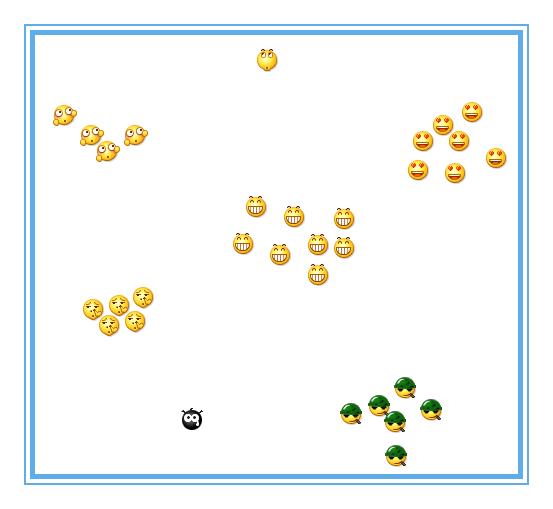
OK，现在就很明显的看出，不同的学生，自己就组成了自己的一个个小团体，这就是所谓的聚类。

那么你作为校长，自然会在脑中脑补，为什么这几个学生会自然的聚在一起呢？肯定是共同的爱好或者共同的目的，至于这个团体，有哪些共同的爱好和共同目的，就是学生之间的某种特征了，比如学习好的会自动凑在一起；或者是喜欢打球的，会凑在一起。

这种，每个学生，与他周围的学生之间，一般有一些共有的某种特征。理论上，如果有一个带有这种特征的学生出现在操场上，那么他身边出现的，就有很大可能与他有同样的特征，而且他们之间会产生潜在的依赖性。比如喜欢打球的学生，一个人肯定没办法打，所以自然需要有共同爱好的小伙伴在旁边。

这种潜在的（因为没有很明显的表现出来，所以肯定是潜在的）的相互依赖性，就是所谓的“空间自相关”。

对空间自相关的研究，是揭示空间数据分布的一个很重要的概念，而对空间自相关中的关联性程度的计算，就是研究空间自相关的主要方法了。

那么，下一期，我们来聊聊衡量空间自相关的最重要的关联程度计算指标之一：Moran’s I（莫兰斯 I）值。