Codeforces Round #799（Div. 4，CF1692）全题解
Posted hans774882968
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Codeforces Round #799（Div. 4，CF1692）全题解相关的知识，希望对你有一定的参考价值。
文章目录
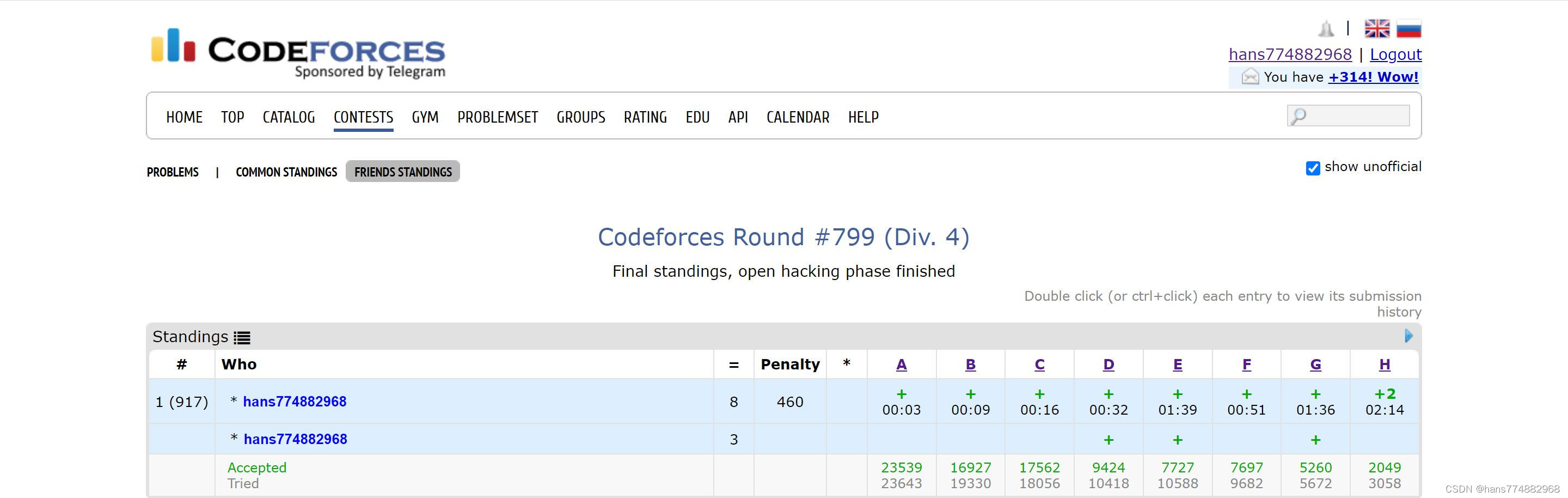
第一次AK CF纪念，虽然只是个div4。以前也有div3差点AK的经历，现在div3难度上来了，这种机会永远不会再有了吧……
为什么E水题写得尤其慢？因为中途洗了个澡。
这套题的概况：应该是最难的一场div4了。A~D不是算法题，E~H是算法题，H的dp有点难，想了我不少时间，差点没过。
作者：hans774882968以及hans774882968
A
签到。
B
设sz是集合大小。n - sz为偶数，则答案恰好为sz，否则需要多删一个元素，答案sz-1。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
#define rep(i,a,b) for(int i = (a);i <= (b);++i)
#define re_(i,a,b) for(int i = (a);i < (b);++i)
#define dwn(i,a,b) for(int i = (a);i >= (b);--i)
const int N = 3e5 + 5;
int n, a[N];
void dbg()
puts ("");
template<typename T, typename... R>void dbg (const T &f, const R &... r)
cout << f << " ";
dbg (r...);
template<typename Type>inline void read (Type &xx)
Type f = 1;
char ch;
xx = 0;
for (ch = getchar(); ch < '0' || ch > '9'; ch = getchar() ) if (ch == '-') f = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar() ) xx = xx * 10 + ch - '0';
xx *= f;
void read()
template<typename T, typename ...R>void read (T &x, R &...r)
read (x);
read (r...);
int main()
int T;
read (T);
while (T--)
read (n);
rep (i, 1, n) read (a[i]);
map<int, int> mp;
rep (i, 1, n) mp[a[i]]++;
printf ("%d\\n", mp.size() - ( (n - mp.size() ) % 2) );
return 0;
C
题意：8*8棋盘，给出bishop的攻击范围，找bishop的位置。
水。当前点和对角线4个邻居都是'#'的点就是。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
#define rep(i,a,b) for(int i = (a);i <= (b);++i)
#define re_(i,a,b) for(int i = (a);i < (b);++i)
#define dwn(i,a,b) for(int i = (a);i >= (b);--i)
const int N = 3e5 + 5;
int n;
char s[15][15];
void dbg()
puts ("");
template<typename T, typename... R>void dbg (const T &f, const R &... r)
cout << f << " ";
dbg (r...);
template<typename Type>inline void read (Type &xx)
Type f = 1;
char ch;
xx = 0;
for (ch = getchar(); ch < '0' || ch > '9'; ch = getchar() ) if (ch == '-') f = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar() ) xx = xx * 10 + ch - '0';
xx *= f;
void read()
template<typename T, typename ...R>void read (T &x, R &...r)
read (x);
read (r...);
int main()
int T;
read (T);
while (T--)
re_ (i, 0, 8) scanf ("%s", s[i]);
rep (i, 1, 6) rep (j, 1, 6)
if (s[i][j] == '#' && s[i - 1][j + 1] == s[i + 1][j + 1] && s[i - 1][j + 1] == s[i - 1][j - 1] && s[i - 1][j + 1] == s[i + 1][j - 1] && s[i - 1][j + 1] == '#')
printf ("%d %d\\n", i + 1, j + 1);
return 0;
D
题意：给出当前时刻（用%02d:%02d表示，如05:50）和delta，表示从当前时刻开始，每delta分钟看一次闹钟，注意该过程是永久的。问总共能看到几个回文时刻。
虽然过程是永久的，但只需要处理到下一次走到当前时刻，即lcm(1440,delta)分钟。这个过程只需要枚举1440 // gcd(1440,delta)次，很稳。
from collections import defaultdict
from math import gcd
def get_time(v):
return "%02d:%02d" % (v // 60, v % 60)
def lcm(a, b):
return a // gcd(a, b) * b
for _ in range(int(input())):
time_s, d = input().split()
d = int(d)
h, m = map(int, time_s.split(':'))
cur = h * 60 + m
ans = 0
las = cur + lcm(1440, d)
for ti in range(cur, las, d):
time_s = get_time(ti % 1440)
if time_s == time_s[::-1]:
ans += 1
print(ans)
E
题意：给出01数组，每次你可以删除数组首元素和末尾元素，问最少删除几次可以得到一个和为s的子数组。如果无法得到输出-1。
双指针老模板题了。枚举所得子数组的右边界r，然后找到最小的l，使得a[l~r]等于s，则r-l+1为一个候选。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
#define rep(i,a,b) for(int i = (a);i <= (b);++i)
#define re_(i,a,b) for(int i = (a);i < (b);++i)
#define dwn(i,a,b) for(int i = (a);i >= (b);--i)
const int N = 3e5 + 5;
int n, s, a[N];
void dbg()
puts ("");
template<typename T, typename... R>void dbg (const T &f, const R &... r)
cout << f << " ";
dbg (r...);
template<typename Type>inline void read (Type &xx)
Type f = 1;
char ch;
xx = 0;
for (ch = getchar(); ch < '0' || ch > '9'; ch = getchar() ) if (ch == '-') f = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar() ) xx = xx * 10 + ch - '0';
xx *= f;
void read()
template<typename T, typename ...R>void read (T &x, R &...r)
read (x);
read (r...);
int main()
int T;
read (T);
while (T--)
read (n, s);
rep (i, 1, n) read (a[i]);
int tot = accumulate (a + 1, a + n + 1, 0);
if (tot < s)
puts ("-1");
continue;
int l = 1, cur = 0, ans = 0;
rep (i, 1, n)
cur += a[i];
if (cur < s)
continue;
while (l < i && cur > s)
cur -= a[l++];
ans = max (ans, i - l + 1);
printf ("%d\\n", n - ans);
return 0;
F
题意：给你一个数组，求是否存在3个不同下标，使得a[i]+a[j]+a[k]以3结尾。
以3结尾，即模10余3，故只需要扔到模10的桶里，然后3重循环枚举。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
#define rep(i,a,b) for(int i = (a);i <= (b);++i)
#define re_(i,a,b) for(int i = (a);i < (b);++i)
#define dwn(i,a,b) for(int i = (a);i >= (b);--i)
const int N = 10 + 5;
int n, a[N];
void dbg()
puts ("");
template<typename T, typename... R>void dbg (const T &f, const R &... r)
cout << f << " ";
dbg (r...);
template<typename Type>inline void read (Type &xx)
Type f = 1;
char ch;
xx = 0;
for (ch = getchar(); ch < '0' || ch > '9'; ch = getchar() ) if (ch == '-') f = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar() ) xx = xx * 10 + ch - '0';
xx *= f;
void read()
template<typename T, typename ...R>void read (T &x, R &...r)
read (x);
read (r...);
bool jdg()
rep (i, 0, 9)
if (!a[i]) continueCodeforces Round #799 (Div. 4)
Codeforces Round #799 (Div. 4)
Codeforces Round #799（Div. 4，CF1692）全题解
Codeforces Round #413, rated, Div. 1 + Div. 2 C. Fountains（贪心 or 树状数组）
Playrix Codescapes Cup (Codeforces Round #413, rated, Div. 1 + Div. 2) C. Fountains 树状数组维护区间最大值(示(代