深度学习：《PyTorch入门到项目实战》卷积神经网络：填充(padding)和步幅(stride)

Posted 2022-06-15 JoJo的数据分析历险记

【深度学习】：《PyTorch入门到项目实战》（十二）填充(padding)和步幅(stride)

• ✨本文收录于【深度学习】：《PyTorch入门到项目实战》专栏，此专栏主要记录如何使用PyTorch实现深度学习笔记，尽量坚持每周持续更新，欢迎大家订阅！
• 🌸个人主页：JoJo的数据分析历险记
• 📝个人介绍：小编大四统计在读，目前保研到统计学top3高校继续攻读统计研究生
• 💌如果文章对你有帮助，欢迎✌关注、👍点赞、✌收藏、👍订阅专栏
• 参考资料：本专栏主要以沐神《动手学深度学习》为学习资料，记录自己的学习笔记，能力有限，如有错误，欢迎大家指正。同时沐神上传了的教学视频和教材，大家可以前往学习。
• 视频：动手学深度学习
• 教材：动手学深度学习

文章目录

• 【深度学习】：《PyTorch入门到项目实战》（十二）填充(padding)和步幅(stride)
• 前言
• 1. padding
• 2.步幅(stride)
• 3.代码实现
• • 3.1 padding实现
  • 3.2 stride实现

前言

在之前，我们介绍了卷积核对输入特征的影响。假设输入特征为$n\times n$,核形状为$f\times f$，那么经过卷积核作用后，得到的输出形状为$(n-f+1)\times (n-f+1)$。可以看出，通常情况下输出特征会由于卷积核的作用而减小。而深度神经网络中，由于卷积核的作用，会导致我们的输出过早的变的很小，导致我们无法构建深层的神经网络。本章介绍另外两个影响输出形状的方法，扩充(padding)和步幅(stride)。

• 有时候，输出远远小于输入，这是因为卷积核的影响，而在原始图像较小的情况下，任意丢失很多信息，这个时候我们需要使用填充是解决此问题。
• 有时，我们可能希望大幅降低图像的宽度和高度。例如，我们发现一个图像实在是太大了。这个时候使用步幅可以快速将输出变小。

1. padding

为了构建深度神经网络，你需要学会使用的一个基本的卷积操作就是padding。首先让我们来回忆一下卷积是如何计算的：

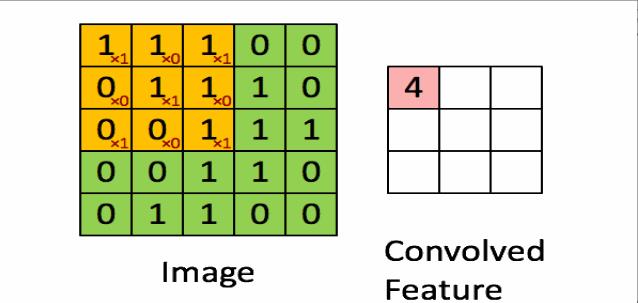
这其实有两个缺陷：

• 第一个是如果每一次使用一个卷积操作，我们的图像都会缩小。 例如我们从 6x6 通过一个 3x3的卷积核，做不了几次卷积，我们的图片就会变得非常小，也许它会缩小到只有1x1。

• 第二个缺陷是图片角落或者边际上的像素只会在输出中被使用一次 因为它只通过那个3x3的过滤器（filter）一次 然而图片中间的一个像素，会有许多3x3的过滤器（filter）在那个像素上重叠 所以相对而言 角落或者边界上的像素被使用的次数少很多，这样我们就丢失了许多图片上靠近边界的信息。

所以为了同时解决上述的两个问题。我们能做的是在使用卷积操作前，对图片进行填充，通常是用0来进行填充，具体如下所示。

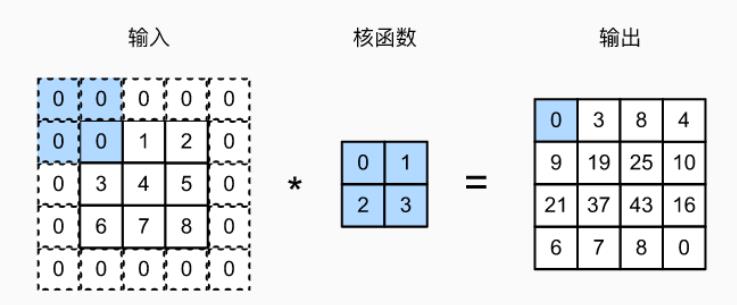
我们可以沿着图像边缘再填充一层像素。这样那么3×3的图像就被我们填充成了一个5×5的图像。如果你用2×2的卷积核对这个5×5的图像卷积，我们得到的输出就不是2×2，而是4×4的图像，你就得到了一个尺寸比原始图像3×3还大图像。习惯上，我们都用用0去填充，如果$p$是填充参数，在这个案例中，$p=1$，因为我们在周围都填充了一个像素点，输出也就变成了$(n+2p-f+1)\times (n+2p-f+1)$。所以，要是我们想要保持图像大小不变，则意味着$2p-f+1=0$,则$p=\frac{f-1}{2}$,在后面我们的卷积核通常会设置为奇数。

为了指定卷积操作中的padding，我们可以指定$p$的值。以上就是padding，下面我们讨论一下如何在卷积中设置步长。

2.步幅(stride)

卷积窗口从输入张量的左上角开始，向下、向右滑动。 在前面的例子中，我们默认每次滑动一个元素。 但是，有时候为了高效计算或是缩减采样次数，卷积窗口可以跳过中间位置，每次滑动多个元素。卷积中的步幅是另一个构建卷积神经网络的基本操作，例如，下面是一个步幅为3的情况。

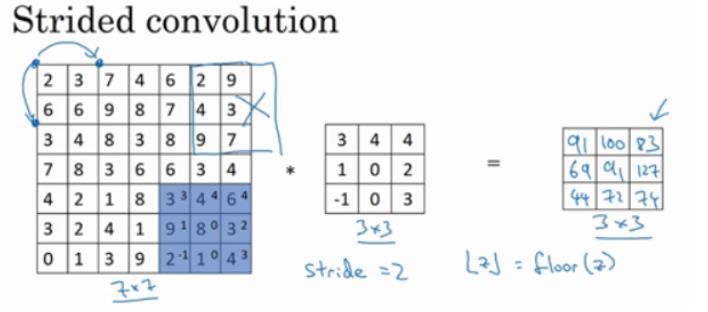
如果我们用一个$f\times f$的过滤器卷积一个$n\times n$的图像，padding为$p$，步幅为$s$，在这个例子中$s=3$，因为现在我们不是一次移动一个步长，而是一次移动$s$步，输出于是变为$[\frac{n+2p-f}{s}+1][\times \frac{n+2p-f}{s}+1]$。[] 表示向下取整。

3.代码实现

3.1 padding实现

在pytorch中，padding和stride的都可以在nn中实现

# 导入相关库
import torch
from torch import nn
# 定义计算卷积层函数
def comp_conv2d(conv2d, X):
    # 这里的（1，1）表示批量大小和通道数都是1
    X = X.reshape((1, 1) + X.shape)
    Y = conv2d(X)
    # 省略前两个维度：批量大小和通道
    return Y.reshape(Y.shape[2:])

# 请注意，padding参数这里每边都填充了1行或1列，因此总共添加了2行或2列
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)#因此这里相当于是一个3×3的kernel加padding=1，那么根据我们的公式可以得到，最终得到的输出和输入一致
X = torch.rand(size=(8, 8))
comp_conv2d(conv2d, X).shape

torch.Size([8, 8])

3.2 stride实现

步幅使用stride参数实现，具体代码如下，设置步幅为2，padding为1，kernel_size为3×3，那么这样根据公式$[\frac{n+2p-f}{s}+1]$这里n为8，p=1，f=3，s=2，会返回一个4×4的输出。

conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)
comp_conv2d(conv2d, X).shape

torch.Size([4, 4])

本章的介绍到此介绍，如果文章对你有帮助，请多多点赞、收藏、评论、关注支持！！