数学知识整理：极值&最值，驻点，拉格朗日乘子

Posted 2022-06-13 UQI-LIUWJ

1 极值

1.1 驻点

• 如果函数z=f(x,y)在点处有极值，且偏微商存在，那么z=f(x,y)在处的偏微商必为0，即
• 称满足的点为函数z=f(x,y)的驻点，也称为平衡点
• z=f(x,y)的极值点必然是它的驻点或者偏微商不存在的点；但是驻点不一定是极值点
  • 比如z=f(x,y)=xy，在(0,0)处显然有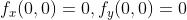，也即(0,0)是f(x,y)的一个驻点，但是(0,0)并不是函数的极值点（只是一个鞍点）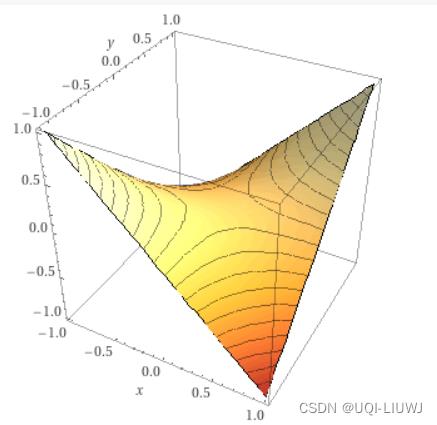

   1.1.1 驻点是极值点的充分条件

设z=f(x,y)在定义域内一点处有二阶连续偏微商，且

我们记 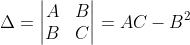，，则

• 当Δ>0,A>0时，f(x,y)在 点处有极小值

• 当Δ>0,A<0时，f(x,y)在 点处有极大值

• 当Δ<0时， f(x,y)在 点处无极值

 2 最值

求函数在区域D上的最值的一般方法是，先求出函数在区域D内部的极值，在于函数在D的边界上的最值进行比较。

 

对于有些问题而言，我们可以知道函数最值存在，且在区域D的内部。如果此时函数在区域D内偏微分存在，且又只有唯一的驻点，那此驻点为最值

3 条件极值

求函数z=f(x,y)满足条件的条件极值

3.1 将条件极值化为普通极值

从条件方程中解出y=g(x),代入z=f(x,y)中

3.2 拉格朗日乘子

（1）写出辅助函数

（2）x,y,λ满足的方程组

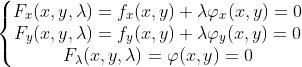
（3）由上述方程组解出的(x,y)就是可能取条件极值的点

求m元函数+n个约束条件同理