深度学习系列36：交叉熵笔记
Posted IE06
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了深度学习系列36：交叉熵笔记相关的知识，希望对你有一定的参考价值。
1 熵
出现概率p越高的信息，编码长度L越短。这样的话，总的编码长度能够最小化。
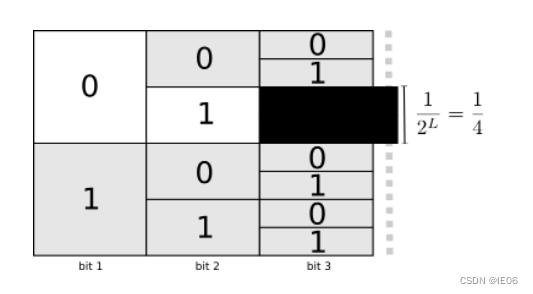
L与p之间的关系可以用下图的二分搜索来展示。概率为p的实体，对应的编码长度为
log
2
1
/
p
\\log_21/p
log21/p能够将期望编码长度最小化。
熵则是编码长度的期望：
H
=
−
p
log
2
p
H = -p\\log_2p
H=−plog2p
2 交叉熵和KL散度
交叉熵用来计算非最优分布的期望编码长度。
与最优编码之间的差值称为KL散度：
D
q
(
p
)
=
H
q
(
p
)
−
H
(
p
)
D_q(p)=H_q(p)-H(p)
Dq(p)=Hq(p)−H(p)
一般预测模型中会使用softmax函数将列表转化为概率分布，用来计算交叉熵。
3. InfoNCE
如果类别特别多，要计算softmax的话会非常耗时，因此改成NCE损失。抽象来说，就是：
原先要计算N分类的概率列表然后结合标签计算交叉熵，现在改成计算标签和预测结果是否匹配的2分类问题（负样本需要随机采样）。
InfoNCE则是将采样出来的k个负样本还是看做k个类，计算交叉熵。InfoNCE loss的任务是一个k+1类的分类任务，目的就是想把样本图片分到标签这个类里。
开发者涨薪指南
48位大咖的思考法则、工作方式、逻辑体系
以上是关于深度学习系列36：交叉熵笔记的主要内容，如果未能解决你的问题，请参考以下文章