bezier曲线的一个计算问题

Posted 2023-03-23

给定四点P1(0,0,0),P2(1,1,1),P3(2,-1,-1),P4(3,0,0)，用其作为特征多边形来构造一条三次Bezier曲线，并计算参数为0，1/3，2/3，1的值。
怎么做啊.谢谢帮忙!!!!!!!!!

参考技术A 编程语言 C++

#include<stdio.h>

void Bezier(int x1,int y1,int z1,int x2,int y2,int z2,int x3,int y3,int z3,int x4,int y4,int z4,float u)
double a[4][4],b[4][4],c[4][4];
a[0][0]=x1;
b[0][0]=y1;
c[0][0]=z1;
a[0][1]=x2;
b[0][1]=y2;
c[0][1]=z2;
a[0][2]=x3;
b[0][2]=y3;
c[0][2]=z3;
a[0][3]=x4;
b[0][3]=y4;
c[0][3]=z4;
for(int i=1;i<=3;i++)
for(int j=0;j<4-i;j++)

a[i][j]=(1-u)*a[i-1][j]+u*a[i-1][j+1];
b[i][j]=(1-u)*b[i-1][j]+u*b[i-1][j+1];
c[i][j]=(1-u)*c[i-1][j]+u*c[i-1][j+1];

printf("%10lf%10lf%10lf\n",a[3][0],b[3][0],c[3][0]);


void main()
int x1,y1,z1,x2,y2,z2,x3,y3,z3,x4,y4,z4;float u;
printf("输入Bezier曲线第控制顶点\n");
scanf("%d%d%d%d%d%d%d%d%d%d%d%d",&x1,&y1,&z1,&x2,&y2,&z2,&x3,&y3,&z3,&x4,&y4,&z4);
for(;;)
fflush(stdin);
printf("输入u=");
scanf("%f",&u);
Bezier(x1,y1,z1,x2,y2,z2,x3,y3,z3,x4,y4,z4,u);

参考资料：自编

12月学习进度6/31——计算机图形学期末准备03Bezier曲线及MATLAB实现

贝塞尔曲线

参考GAMES101计算机图形学视频
↑
讲得超级棒！

定义

Bezier曲线 —— 用给定的控制点定义曲线，控制点控制曲线的弯曲，不一定要全部经过所有控制点

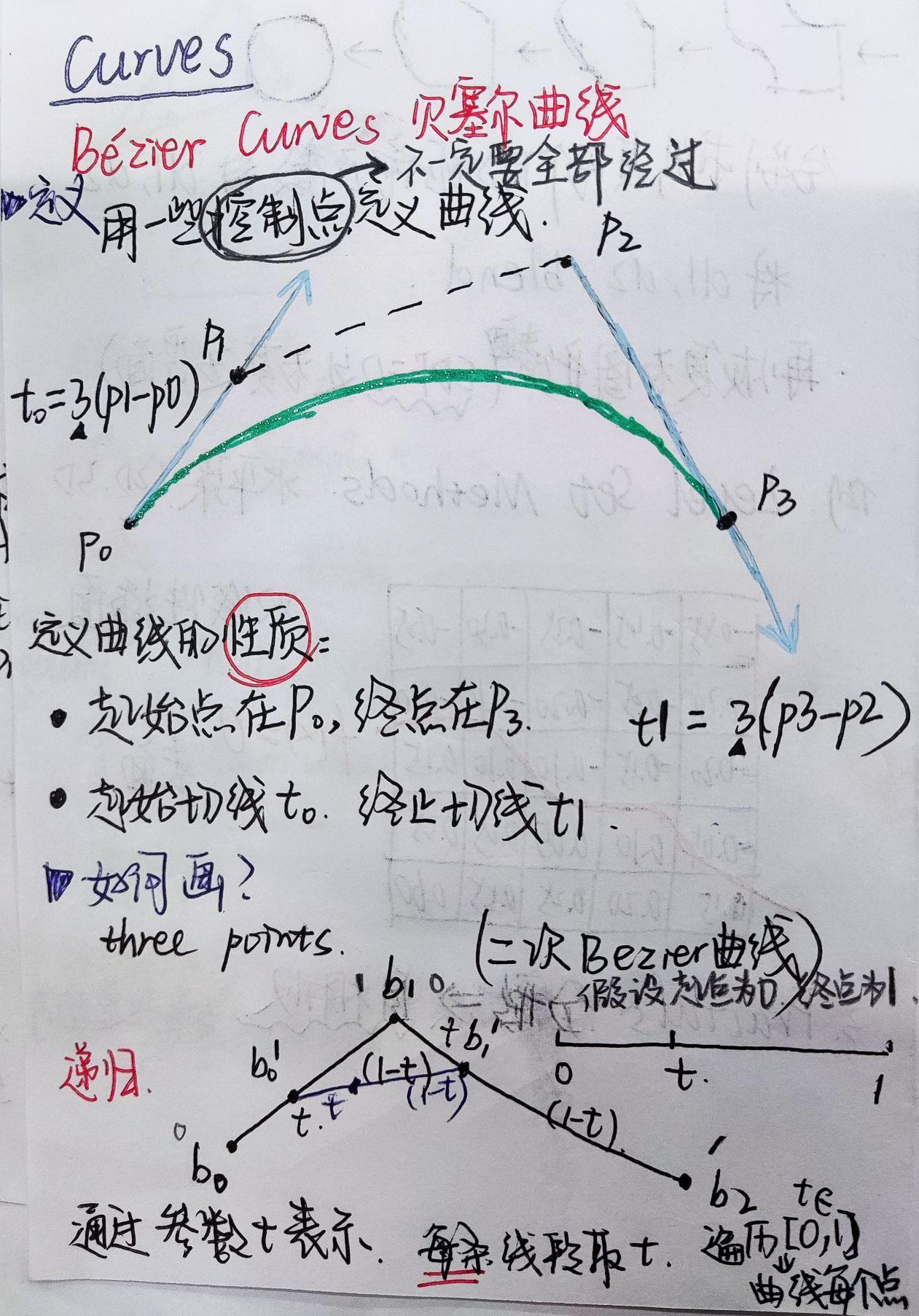
1.如何画Bezier曲线（递归过程）

参数 $t\in [0,1]$
对于每一个 $t$ ：

1. 针对每一个控制点所连的线段 $b_i{b}_{i+1}$ 取点 $b_i^{\prime }$，使得:
   • $|b_i{b}_i^{\prime }|=t$
   • $|b_i^{\prime }{b}_{i+1}|=1-t$
2. 连接 $b_i^{\prime }$ 和 $b_{i+1}^{\prime }$ ，新构成的所有线段，重复上述取点 $b_i^{\prime \prime }$ 操作
3. 重复1,2操作，直到线段数为1，则该线段上取的点就是该 $t$ 对应的曲线上的点

遍历所有 $t\in [0,1]$ ，则可以画出该组控制点对应的Bezier曲线

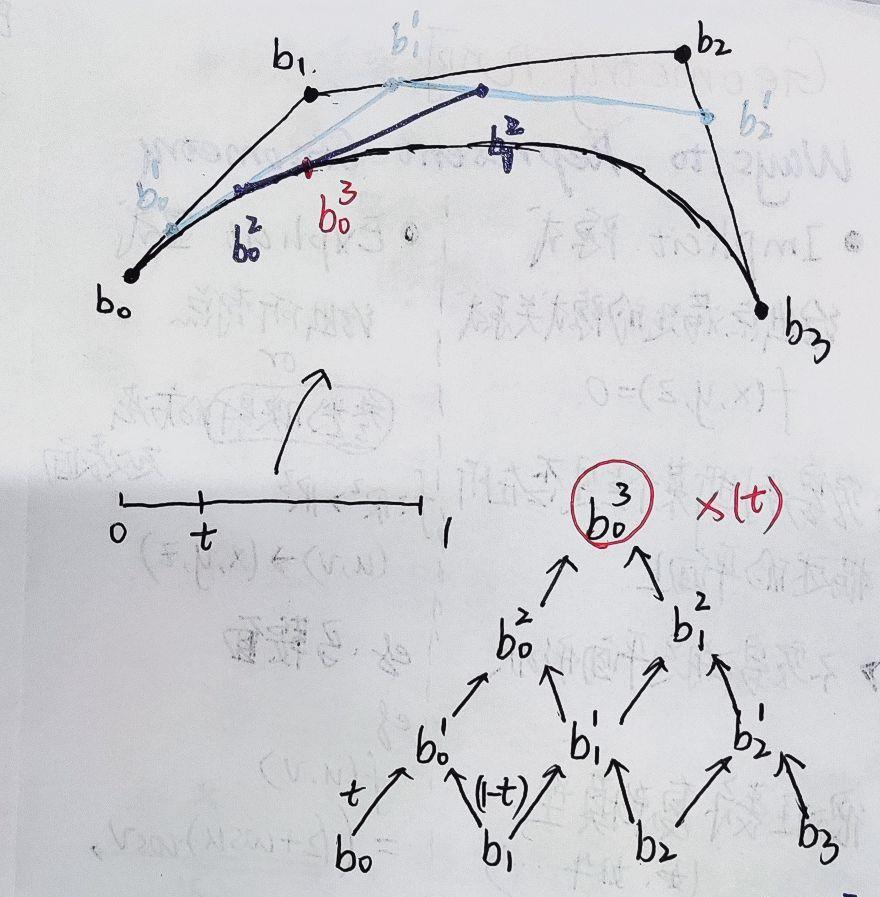
2.Bezier曲线的代数形式

$b^n(t)={\Sigma }_{j=0}^n{b}_j\ast B_j^n(t)$

其中 $B_j^n(t)=C_n^i\ast t^i\ast (1-t{)}^{n-i}$
多项式对称： $C_n^i=C_n^{n-i}$

该公式可看做：

1. 控制点 $b_j$ 对多项式 $B_j^n(t)$ 的加权和；
2. 多项式 $B_j^n(t)$ 对控制点 $b_j$ 的加权和；

Bezier曲线的性质

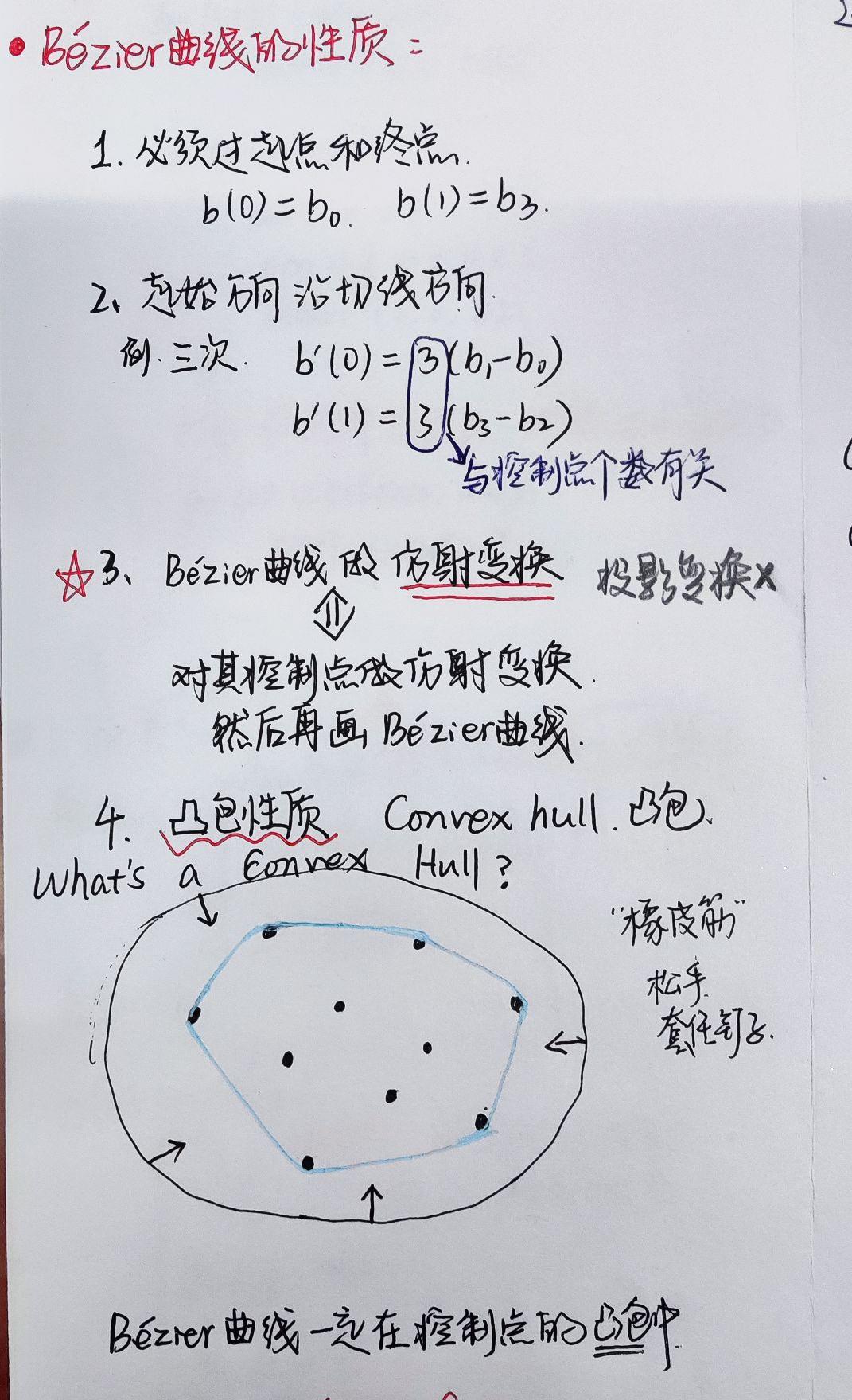
Bezier曲线一定在其控制点的凸包中：
当控制点共线时 → 形成的Bezier曲线就是这条直线

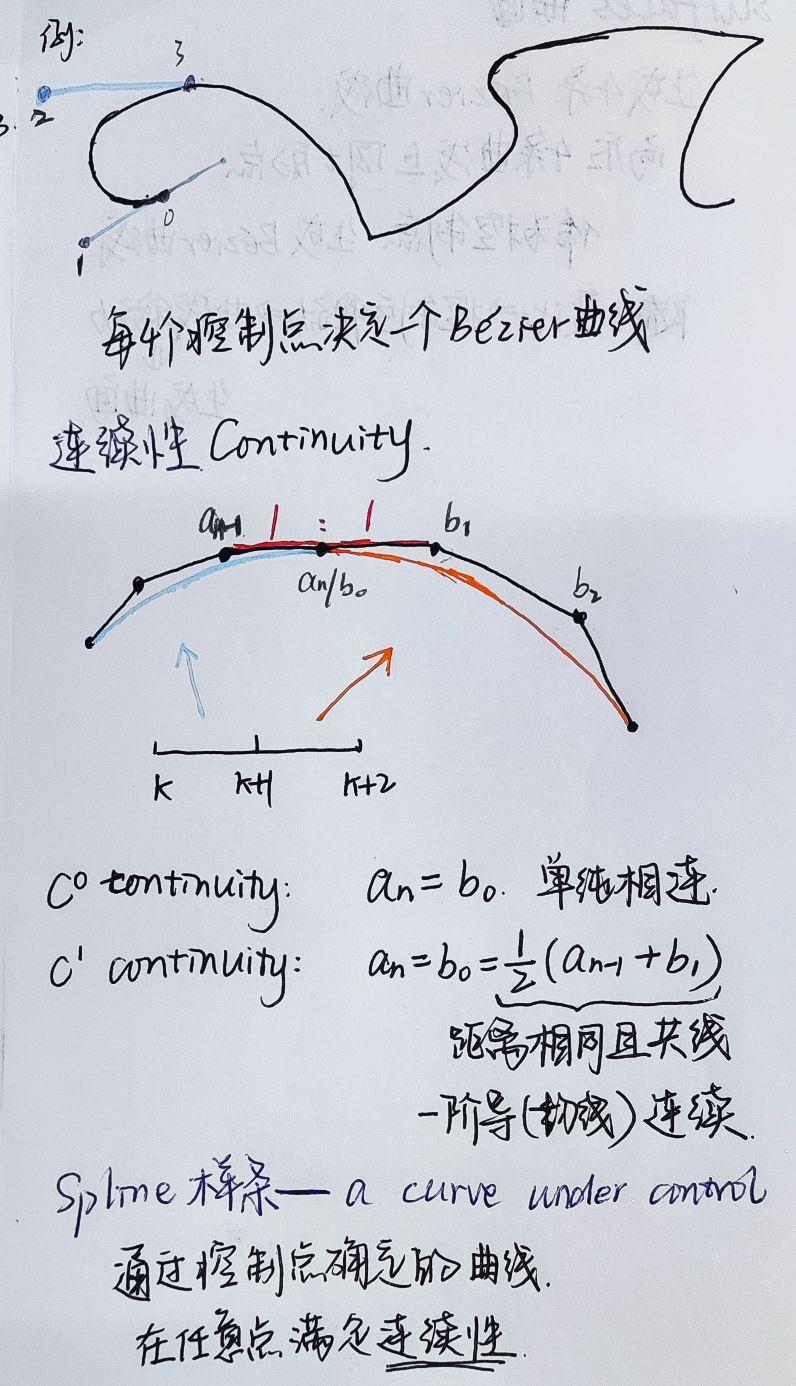
分段Bezier曲线及连续性

当控制点较多时，不好控制，曲线较平滑，单个控制点的改变对曲线形状影响较小
常用：三次Bezier曲线（4个控制点）

矩阵形式表示

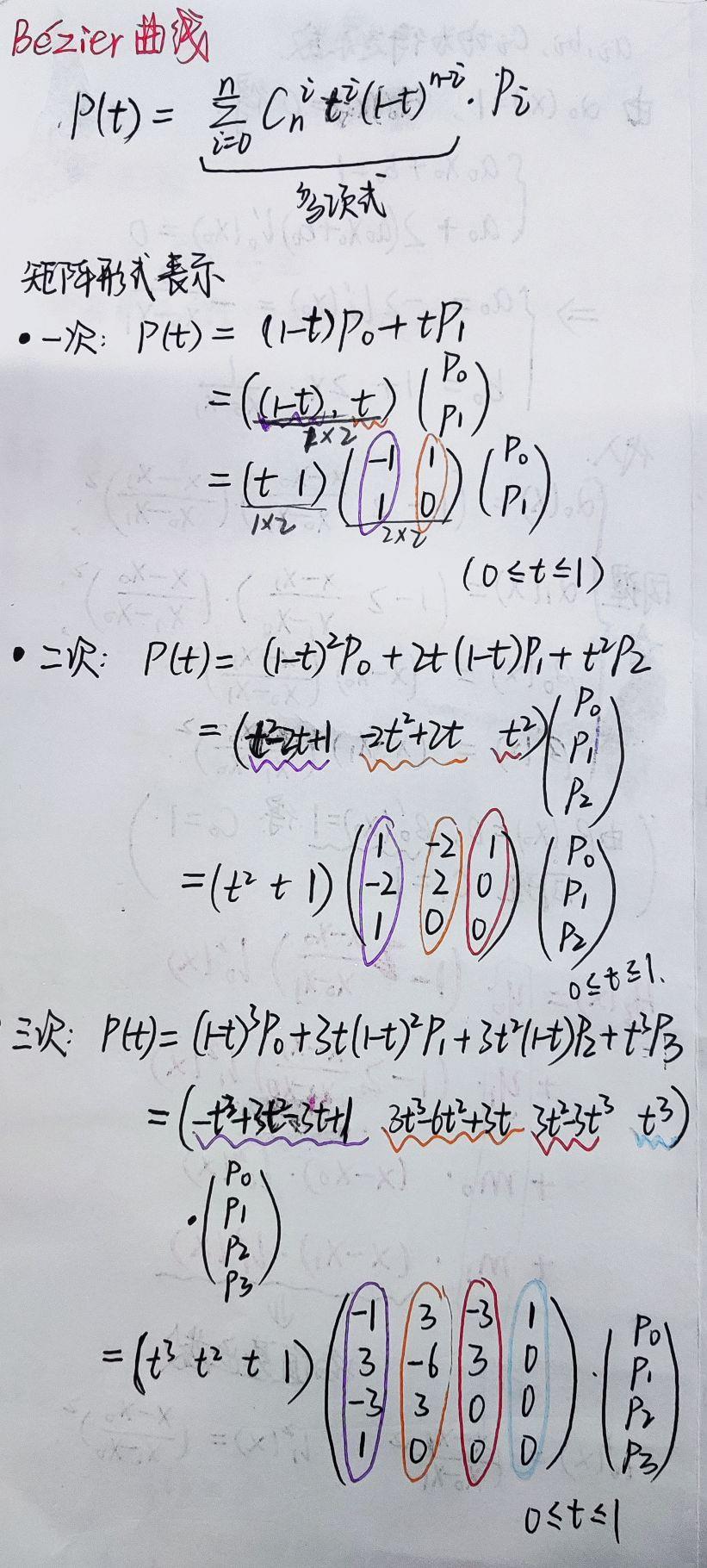
MATLAB实现（二维点）

function bezier(p0,p1,p2,p3)
%p0-p3是控制点
x_t = [];%存放曲线上x的坐标
y_t = [];%存放曲线上y的坐标
A = [-1 3 -3 1;3 -6 3 0;-3 3 0 0;1 0 0 0];
%三次的矩阵表示
for t = 0:0.001:1
    %遍历每个t
    x_it = [t^3 t^2 t 1] * A * [p0(1);p1(1);p2(1);p3(1)];
    y_it = [t^3 t^2 t 1] * A * [p0(2);p1(2);p2(2);p3(2)];
    x_t = [x_t,x_it]; %将本次计算的结果加入到结果矩阵中
    y_t = [y_t,y_it];
end
 
plot(x_t,y_t);

【例子】
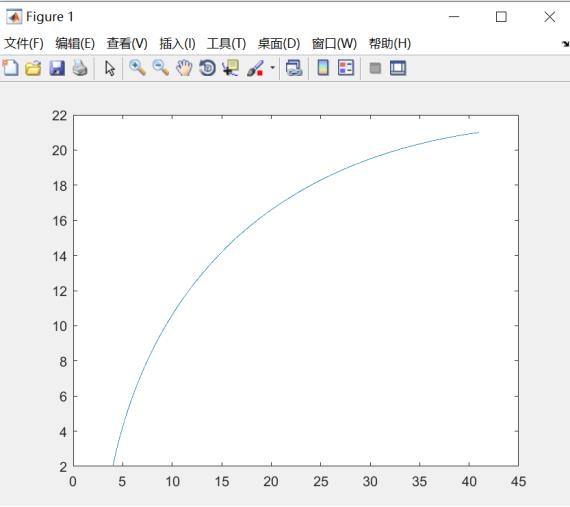
example 1:

p0 = [4 2];
p1 = [7 10];
p2 = [16 19];
p3 = [41 21];
bezier(p0,p1,p2,p3);

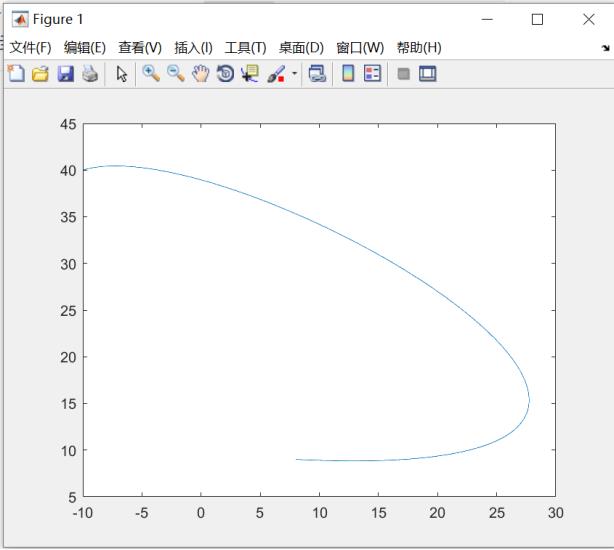
example 2:

p0=[-10,40];
p1=[3,45];
p2=[56,6];
p3=[8,9];
bezier(p0,p1,p2,p3);