学习笔记图神经网络库 DGL 入门教程（backend pytorch）

Posted 2022-05-19 囚生CY

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了学习笔记图神经网络库 DGL 入门教程（backend pytorch）相关的知识，希望对你有一定的参考价值。

dgl库笔记

DGL官方文档

DGL是目前非常流行的用于以知识图谱为代表的图神经网络研究的python包，在阅读项目代码GitHub@RE-Net 时发现该库非常重要, 几乎目前涉及GNN训练的情况需要使用该库进行网络搭建, 该项目代码的相关论文摘要参考【论文阅读】时间序列中的变量是一张知识图谱 ; 这篇paper目前应该算是时序知识图谱中的标杆, 它的模型评估是当前最好的, 主要使用的是自回归的神经网络以及一个RGCN的近邻聚合器;

笔者在本机CPU上跑通代码后开始尝试去跑GPU, 发现4G显存完全吃不住, 连预训练的部分都无法跑通, 于是决定先看一遍DGL官方文档 ; 不得不说这个User Guide真的写得实在是太好了, 区别于那些只是把接口函数的调用说明列得老长老长的库(比如torch, sklearn, 还有tensorflow), DGL的User Guide层次清晰, 以图神经网络的搭建到训练的任务时间线为线索, 非常详细地介绍了如何使用DGL, 并且这篇User Guide更像是一篇综述性质地paper, 学一遍不仅是对GNN能有所了解, 而且对很多方法, 如消息传递, 近邻采样的数学原理也能了解, 图文并茂, 实乃不可多得的资源;

本文笔者主要是对DGL官方文档的一个翻译, 截至本文发布, Chapter1-4部分官方文档已经有了中文翻译, 笔者在此基础上添加了一些个人理解的备注, 以供查阅; Chapter5-7目前只有英文, 笔者主要是做了一些翻译和备注, 使得阅读起来更加容易;

注意: 本文全部是以pytorch为后端的DGL使用;

PS:

tensorflow可能并不是DGL的最佳选择, 在Chapter 7中可以看到, 分布式训练仅仅支持pytorch, 而无法使用tensorflow作为后端实现, 看来Google圈地自萌在自己的TPU上搞早晚是要与主流脱节了… (笔者瞎猜的…);
此外本文的学习本质上也是对torch的一个巩固, 其实DGL里面很多数据处理, 训练模型, 模型搭建, 包括自定义模块都与torch是类似的, 总之强烈推荐去看一遍官方文档, 笔者大概前后看了整整两天, 个人认为花时间完整过一遍一定不会吃亏的;
目录里的杂记章节可能会不定期更新;

dgl库笔记
1 DGL的安装
2 DGL的后端
3 一个有趣的入门示例
- 3.1 从"Zachary's karate club" Problem讲起
- 3.2 第一步: 使用DGL创建图
- 3.3 第二步: 为图的边和图的节点赋值
- 3.4 第三步: 定义图卷积网络(GCN)
- 3.5 第四步: 数据预处理与初始化
- 3.6 第五步: 图模型训练与可视化
Chapter 1: 图
- 1.1 关于图的基本概念
- 1.2 图, 节点和边
- 1.3 节点与边的特征
- 1.4 从外部源创建图
- 1.5 异构图
- 1.6 在GPU上使用DGLGraph
Chapter 2: 消息传递
- 2.1 内置的消息传递接口函数
- 2.2 如何编写高效的消息传递代码
- 2.3 在图的一部分上进行消息传递
- 2.4 在消息传递中使用边权重
- 2.5 在异构图上进行消息传递
Chpater 3: 构建图神经网络(GNN)模块
- 3.1 dgl.nn模块的构造函数
- 3.2 编写dgl.nn模块的forward函数
- 3.3 异构图上的GraphConv模块
Chapter 4: 图数据管道
- 4.1 DGLDataset类
- 4.2 下载原始数据(可选)
- 4.3 数据处理
- 4.4 保存与加载数据
- 4.5 使用ogb库加载OGB数据集
Chapter 5: 训练图神经网络(GNN)
- 5.1 节点分类/回归
- 5.2 边分类/回归
- 5.3 链接预测
- 5.4 整图分类
Chapter 6: 大规模图上的随机训练
- 6.1 训练GNN来进行近邻采样的节点分类
- 6.2 训练GNN来进行近邻采样的边分类
- 6.3 训练GNN来进行近邻采样的链接预测
- 6.4 自定义近邻采样器
- 6.5 实现用于mini-batch训练的自定义GNN模块
- 6.6 大规模图上的精确线下推断
Chapter 7: 分布式训练
- 7.1 分布式训练的预处理
- 7.2 分布式接口函数
- 7.3 分布式训练的一些工具
杂记
- 1 dgl.DGLGraph.add_edges
- 2 关于dgl创建图的本质
- 专题一消息传递函数
- - 小节附录: 消息函数杂记
附录: 接口索引

1 DGL的安装

DGL官方文档的安装方法似乎有些繁琐, 直接下载wheel文件安装即可;

非CUDA版本的dgl库, 去清华镜像dgl仓库下载对应版本的whl文件直接用pip install安装即可;
CUDA版本的dgl库, 目前有五种不同的dgl库对应不同的CUDA版本:

清华镜像dgl-cu90仓库 ;
清华镜像dgl-cu92仓库 ;
清华镜像dgl-cu100仓库 ;
清华镜像dgl-cu101仓库 ;
清华镜像dgl-cu102仓库 ;
备注:
- 安装所有依赖CUDA的库之前一定先把CUDA安装好, dgl直接在库命名上就给定了对应的CUDA版本, tensorflow-gpu则还要查表看不同版本库需要的CUDA支持标准, torch和torchvision可以在https://download.pytorch.org/whl/torch_stable.html 下载, 该repository中也注明了对应的CUDA版本;
- 虽然不同库对CUDA版本的依赖会有区别, 但是总之CUDA版本越高越好, 低版本的CUDA早晚会被淘汰, dgl最低都到CUDA9.0了, tensorflow-gpu从2.0.0开始就至少需要CUDA10.0, 所以建议跑GPU的PC机就不要装乱七八糟的软件了, 不如多装几个版本的CUDA来得实在; 现在CUDA安装配置还挺快捷, 笔者WIN10+1650Ti显卡(N卡)+固态硬盘的配置十几分钟就能装配好一个版本的CUDA, 而且从NVIDIA官网下载安装包似乎非常快, 3G左右的离线安装包用半小时不到就能下载好, 似乎是有国内代理, 比以前靠谱多了;

2 DGL的后端

通过修改C:\\Users\\caoyang\\.dgl\\config.json中的配置值可以修改dgl库的默认后端, 一般来说就pytorch和tensorflow两种, DGL官方文档额外提到一种MXNet的后端, 不过它后面的章节基本上以pytorch为例写的, 其他两种后端都没有怎么提及, 看起来似乎torch的势头有点反超tensorflow, Google的tensorflow在自己的TPU上圈地自萌, 把N卡A卡让给其他开源开发者, 总之笔者是觉得tensorflow越来越不好用了, 各种意义上的不好用… 而且近期看得几篇近一年内发表的paper, 项目代码都是基于torch写的, 见仁见智吧, 对于打工人可能也只有全都学一条路可走…

3 一个有趣的入门示例

DGL官方文档给了一个非常有趣的入门示例;

3.1 从"Zachary’s karate club" Problem讲起

如下图所示, “Zachary’s karate club” Problem定义在一个包括34个成员的空手道俱乐部里的社交网络上, 俱乐部分为两个社区, 由教员(节点0)和俱乐部主席(节点33)领导, 分别以不同颜色的圆点表示, 问题目标是希望能够预测出每个成员将更倾向于加入哪一个社区;

"Zachary’s karate club" Problem 图描述:

3.2 第一步: 使用DGL创建图

DGL定义图的方法并非常见的邻接矩阵或出入度链表形式, 而是直接将所有边的出节点和入节点用两个list存储, 这样的好处是对于稀疏图(即邻接矩阵系数)可以大大减少存储成本, 且无需额外记录图的节点, 直接将两个list拼接后去重就可以得到所有节点, 不过离群点(出度与入度都为零的节点)是不会被考虑进来的;

建图代码如下所示:

import dgl
import numpy as np

def build_karate_club_graph():
	# All 78 edges are stored in two numpy arrays. One for source endpoints
	# while the other for destination endpoints.
	src = np.array([1, 2, 2, 3, 3, 3, 4, 5, 6, 6, 6, 7, 7, 7, 7, 8, 8, 9, 10, 10,
		10, 11, 12, 12, 13, 13, 13, 13, 16, 16, 17, 17, 19, 19, 21, 21,
		25, 25, 27, 27, 27, 28, 29, 29, 30, 30, 31, 31, 31, 31, 32, 32,
		32, 32, 32, 32, 32, 32, 32, 32, 32, 33, 33, 33, 33, 33, 33, 33,
		33, 33, 33, 33, 33, 33, 33, 33, 33, 33])
	dst = np.array([0, 0, 1, 0, 1, 2, 0, 0, 0, 4, 5, 0, 1, 2, 3, 0, 2, 2, 0, 4,
		5, 0, 0, 3, 0, 1, 2, 3, 5, 6, 0, 1, 0, 1, 0, 1, 23, 24, 2, 23,
		24, 2, 23, 26, 1, 8, 0, 24, 25, 28, 2, 8, 14, 15, 18, 20, 22, 23,
		29, 30, 31, 8, 9, 13, 14, 15, 18, 19, 20, 22, 23, 26, 27, 28, 29, 30,
		31, 32])
	# Edges are directional in DGL; Make them bi-directional.
	u = np.concatenate([src, dst])
	v = np.concatenate([dst, src])
	# Construct a DGLGraph
	return dgl.DGLGraph((u, v))

G = build_karate_club_graph()
print('We have %d nodes.' % G.number_of_nodes())
print('We have %d edges.' % G.number_of_edges())

输出结果:
```
We have 34 nodes.
We have 156 edges.
```

使用networkx对图进行可视化:

如果希望在jupyter notebook中显示nx.draw()得到的绘图结果, 需要在代码中添加%matplotlib inline注解;

可视化代码如下所示:

import networkx as nx
%matplotlib inline
# Since the actual graph is undirected, we convert it for visualization
# purpose.
nx_G = G.to_networkx().to_undirected()
# Kamada-Kawaii layout usually looks pretty for arbitrary graphs
pos = nx.kamada_kawai_layout(nx_G)
nx.draw(nx_G, pos, with_labels=True, node_color=[[.7, .7, .7]])

可视化结果:

3.3 第二步: 为图的边和图的节点赋值

DGLGraph图的边和节点都可以进行赋值, 所谓赋值可以理解为添加特征, 特征当然可以不止一个, 下面的示例是给所有节点添加名为feat的特征, 如果需要给边赋值则将ndata替换为edata即可;

代码示例:

# In DGL, you can add features for all nodes at once, using a feature tensor that
# batches node features along the first dimension. The code below adds the learnable
# embeddings for all nodes:

import torch
import torch.nn as nn
import torch.nn.functional as F

embed = nn.Embedding(34, 5)  # 34 nodes with embedding dim equal to 5
G.ndata['feat'] = embed.weight

# print out node 2's input feature
print(G.ndata['feat'][2])

# print out node 10 and 11's input features
print(G.ndata['feat'][[10, 11]])

输出结果:

tensor([ 0.4228, -1.1062, -0.1551,  1.1317,  0.9008], grad_fn=<SelectBackward>)
tensor([[ 0.3872,  0.9674, -0.0219,  0.3755, -0.6305],
		[-0.7338, -0.4529,  1.1352, -0.6787, -1.0478]],
	   grad_fn=<IndexBackward>)

3.4 第三步: 定义图卷积网络(GCN)

图卷积网络(Graph Convolutional Network, 下简称为GCN)最初在https://arxiv.org/abs/1609.02907 被提出, 简而言之就是在GCN的第 $l$ 层, 图中每个节点 $v_i^l$ 都会带有一个特征向量 $h_i^l$ , 然后每个节点会通过图中的有向边进行特征传输, 一个最简单的例子如下图所示, 即每个节点的特征值更新为所有指向它的节点的特征值之和, 然后使用一个激活函数 $f$ 映射后的结果:

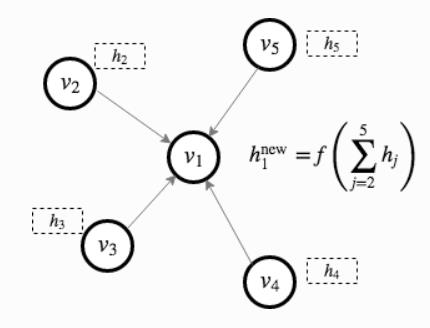
这其中就包含了一个消息传递的概念, 在DGL官方文档中有详细说明;

创建GCN的示例代码:

from dgl.nn.pytorch import GraphConv

class GCN(nn.Module):
	def __init__(self, in_feats, hidden_size, num_classes):
		super(GCN, self).__init__()
		self.conv1 = GraphConv(in_feats, hidden_size)
		self.conv2 = GraphConv(hidden_size, num_classes)

	def forward(self, g, inputs):
		h = self.conv1(g, inputs)
		h = torch.relu(h)
		h = self.conv2(g, h)
		return h

# The first layer transforms input features of size of 5 to a hidden size of 5.
# The second layer transforms the hidden layer and produces output features of
# size 2, corresponding to the two groups of the karate club.
net = GCN(5, 5, 2)

3.5 第四步: 数据预处理与初始化

简单定义所有的节点编号以及分类标签的编号, 以及模型的输入初始值inputs;

inputs = embed.weight
labeled_nodes = torch.tensor([0, 33])  # only the instructor and the president nodes are labeled
labels = torch.tensor([0, 1])  # their labels are different

3.6 第五步: 图模型训练与可视化

模型训练本质与torch模型训练没有区别, 代码与输出结果如下所示:

训练代码示例:

import itertools

optimizer = torch.optim.Adam(itertools.chain(net.parameters(), embed.parameters()), lr=0.01)
all_logits = []
for epoch in range(50):
	logits = net(G, inputs)
	# we save the logits for visualization later
	all_logits.append(logits.detach())
	logp = F.log_softmax(logits, 1)
	# we only compute loss for labeled nodes
	loss = F.nll_loss(logp[labeled_nodes], labels)

	optimizer.zero_grad()
	loss.backward()
	optimizer.step()

	print('Epoch %d | Loss: %.4f' % (epoch, loss.item()))

输出结果:

Epoch 0 | Loss: 0.8385
Epoch 1 | Loss: 0.8092
Epoch 2 | Loss: 0.7829
Epoch 3 | Loss: 0.7614
Epoch 4 | Loss: 0.7426
Epoch 5 | Loss: 0.7266
Epoch 6 | Loss: 0.7128
Epoch 7 | Loss: 0.6996
Epoch 8 | Loss: 0.6895
Epoch 9 | Loss: 0.6809
Epoch 10 | Loss: 0.6723
Epoch 11 | Loss: 0.6639
Epoch 12 | Loss: 0.6555
Epoch 13 | Loss: 0.6467
Epoch 14 | Loss: 0.6376
Epoch 15 | Loss: 0.6282
Epoch 16 | Loss: 0.6188
Epoch 17 | Loss: 0.6095
Epoch 18 | Loss: 0.5996
Epoch 19 | Loss: 0.5893
Epoch 20 | Loss: 0.5783
Epoch 21 | Loss: 0.5670
Epoch 22 | Loss: 0.5552
Epoch 23 | Loss: 0.5430
Epoch 24 | Loss: 0.5300
Epoch 25 | Loss: 0.5170
Epoch 26 | Loss: 0.5037
Epoch 27 | Loss: 0.4903
Epoch 28 | Loss: 0.4767
Epoch 29 | Loss: 0.4621
Epoch 30 | Loss: 0.4471
Epoch 31 | Loss: 0.4316
Epoch 32 | Loss: 0.4163
Epoch 33 | Loss: 0.4006
Epoch 34 | Loss: 0.3838
Epoch 35 | Loss: 0.3662
Epoch 36 | Loss: 0.3481
Epoch 37 | Loss: 0.3295
Epoch 38 | Loss: 0.3103
Epoch 39 | Loss: 0.2908
Epoch 40 | Loss: 0.2716
Epoch 41 | Loss: 0.2526
Epoch 42 | Loss: 0.2339
Epoch 43 | Loss: 0.2157
Epoch 44 | Loss: 0.1981
Epoch 45 | Loss: 0.1812
Epoch 46 | Loss: 0.1647
Epoch 47 | Loss: 0.1483
Epoch 48 | Loss: 0.1326
Epoch 49 | Loss: 0.1179

可视化方法:

画出训练时单个Epoch的图结构:

import matplotlib.animation as animation
import matplotlib.pyplot as plt

def draw(i):
	cls1color = '#00FFFF'
	cls2color = '#FF00FF'
	pos = 
	colors = []
	for v in range(34):
		pos[v] = all_logits[i][v].numpy()
		cls = pos[v].argmax()
		colors.append(cls1color if cls else cls2color)
	ax.cla()
	ax.axis('off')
	ax.set_title('Epoch: %d' % i)
	nx.draw_networkx(nx_G.to_undirected(), pos, node_color=colors,
			with_labels=True, node_size=300, ax=ax)

fig = plt.figure(dpi=150)
fig.clf()
ax = fig.subplots()
draw(0)  # draw the prediction of the first epoch
plt.close()

绘图结果:
通过添加下面的代码可以实现动态图(但是笔者并没有实现怎么动态化… 可能是jupyter notebook缺少相应插件):
```
ani = animation.FuncAnimation(fig, draw, frames=len(all_logits), interval=200)
```

Chapter 1: 图

1.1 关于图的基本概念

详见DGL官方文档文字描述;

这里主要有同构图(homogeneous graph)和异构图(heterogeneous graph)两个概念需要注意, 这在paper里是经常会被提到的;

大部分深度学习考虑的问题通过数学抽象得到的图都是异构图, 即不同的节点会有不同的属性, 不同的边代表不同的含义, 最常见的异构图就是由RDF三元组 $(s, r, o)$ 构建的知识图谱, 每个节点表示不同的实体, 由不同的嵌入表示, 不同的边表示不同的实体关系;
同构图相对简单, 每个节点和每条边本质上都是相同的, 如在考虑社交网络分布时, 每个人都被同等的看待, 关系也视为单纯的社交关系, 一般来说像运筹优化领域的最大流, 旅行商等问题的抽象都是可以视为是一种同构图, 可以通过数学方法进行求解; 通常一个运筹优化问题从同构图拓展到异构图上就会变得复杂无比…
异构图在本章第5节被详细描述;

1.2 图, 节点和边

正如在入门示例章节中提到的那样, dgl库通过存储所有边的出入节点来构建图, 节点一般使用自然数进行编号;
使用dgl.graph()可以创建一个DGLGraph对象, 本章第4节介绍了从其他图网络库的实例化对象直接构建图的方法(如networkx库);

创建图示例代码:

import dgl
import torch as th
# edges 0->1, 0->2, 0->3, 1->3
u, v = th.tensor([0, 0, 0, 1]), th.tensor([1, 2, 3, 3])
g = dgl.graph((u, v))
print(g) # number of nodes are inferred from the max node IDs in the given edges
# Node IDs
print(g.nodes())
# Edge end nodes
print(g.edges())
# Edge end nodes and edge IDs
print(g.edges(form='all'))
# If the node with the largest ID is isolated (meaning no edges),
# then one needs to explicitly set the number of nodes
g = dgl.graph((u, v), num_nodes=8)

输出结果:

Graph(num_nodes=4, num_edges=4,
	  ndata_schemes=
	  edata_schemes=)
tensor([0, 1, 2, 3])
(tensor([0, 0, 0, 1]), tensor([1, 2, 3, 3]))
(tensor([0, 0, 0, 1]), tensor([1, 2, 3, 3]), tensor([0, 1, 2, 3]))

特别地, 可以通过为每条边都创建两个方向的边, 来实现定义无向图, 此时可以使用dgl.to_bidirected()函数来实现这个目的, 该函数可以把原图转换成一个包含反向边的图;

反向图示例代码:
```
bg = dgl.to_bidirected(g)
bg.edges()
```

输出结果:

(tensor([0, 0, 0, 1, 1, 2, 3, 3]), tensor([1, 2, 3, 0, 3, 0, 0, 1]))

最后教程提到尽量使用tensor作为dgl.graph()的参数输入, 不过也支持array和list进行快速测试, 前者相对来说在资源处理上更优化; 且可以通过配置dgl.graph()的参数idtype来修正图存储的数据类型, 比如将默认值int64改为int32就可以大大节约存储空间; 具体数据类型转换如下所示:

数据类型示例代码:

edges = th.tensor([2, 5, 3]), th.tensor([3, 5, 0])  # edges 2->3, 5->5, 3->0
g64 = dgl.graph(edges)  # DGL uses int64 by default
print(g64.idtype)
g32 = dgl.graph(edges, idtype=th.int32)  # create a int32 graph
g32.idtype
g64_2 = g32.long()  # convert to int64
g64_2.idtype
g32_2 = g64.int()  # convert to int32
g32_2.idtype

输出结果:

torch.int64
torch.int32
torch.int64
torch.int32

相关接口方法:

dgl.graph();
dgl.DGLGraph.nodes();
dgl.DGLGraph.edges();
dgl.to_bidirected();
dgl.DGLGraph.int();
dgl.DGLGraph.long();
dgl.DGLGraph.idtype;

1.3 节点与边的特征

正如入门示例中提到的那样, 每个特征都会由一个特征名, 以类似字典的形式存储在DGLGraph对象的ndata和edata中:

节点与边的特征定义代码示例:

import dgl
import torch as th
g = dgl.graph(([0, 0, 1, 5], [1, 2, 2, 0])) # 6 nodes, 4 edges
print(g)
g.ndata['x'] = th.ones(g.num_nodes(), 3)               # node feature of length 3
g.edata['x'] = th.ones(g.num_edges(), dtype=th.int32)  # scalar integer feature
print(g)
# different names can have different shape以上是关于学习笔记图神经网络库 DGL 入门教程（backend pytorch）的主要内容，如果未能解决你的问题，请参考以下文章 
 CUDA 下 DGL 库安装
 比较图神经网络PyTorch Geometric 与 Deep Graph Library，帮助团队选出适合的GNN库
 基于注意力机制的图神经网络且考虑关系的R-GAT的一些理解以及DGL代码实现
 图卷积神经网络GCN的一些理解以及DGL代码实例的一些讲解
 DGL的图数据结构的创建图的特征dgl.batch及一些理解
 Tree-LSTM的一些理解以及DGL代码实现

学习笔记图神经网络库 DGL 入门教程（backend pytorch）

dgl库笔记

目录

1 DGL的安装

2 DGL的后端

3 一个有趣的入门示例

3.1 从"Zachary’s karate club" Problem讲起

3.2 第一步: 使用DGL创建图

3.3 第二步: 为图的边和图的节点赋值

3.4 第三步: 定义图卷积网络(GCN)

3.5 第四步: 数据预处理与初始化

3.6 第五步: 图模型训练与可视化

Chapter 1: 图

1.1 关于图的基本概念

1.2 图, 节点和边

1.3 节点与边的特征