论文阅读基于层级关系的词向量：双曲空间词嵌入

Posted 2022-05-19 囚生CY

树状/层级架构的实体集合有其本身特殊的性质，一般的欧式空间的向量表达难以切实表达每个节点间的关系，从而很难在后续的训练中挖掘实体间的关系。因此有些人开始试图在非欧空间中进行词向量建模，双曲空间由于其与树状结构相恰的特殊几何性质，是目前诸如社交网络等复杂网络图节点的嵌入的主流度量空间，本文主要在文档级别的命名实体识别上比较了双曲空间与欧氏空间词向量的效果。
其实之前旁听过一些组会了解过这种基于上下文建模词向量的方法，似乎还是有很大局限性的，总之深度学习这块的方法都挺玄学。

论文标题：Fine-Grained Entity Typing in Hyperbolic Space
论文下载地址：https://arxiv.org/abs/1906.02505
项目地址：https://github.com/AmitMY/chimera

Step-by-Step: Fine-Grained Entity Typing in Hyperbolic Space
论文下载地址：https://arxiv.org/abs/1906.02505
项目地址: https://github.com/AmitMY/chimera

目录

• 摘要 Abstract
• 1. 引入 Introduction
• 2. 背景: 庞加莱嵌入 Background: Poincare Embeddings
• 3. 双曲空间中的实体类别 Entity Typing in Hyperbolic Space
• • 3.1 任务定义 Task Definition
  • 3.2 目标 Objective
  • 3.3 方法 Method
  • 3.4 实体与上下文表示 Mention and Context Representations
  • 3.5 映射到球 Projection into the Ball
  • 3.6 模型优化 Optimization of the Model
• 4. 层级类别集合 Hierarchical Type Inventory
• • 4.1 数据 Data
  • 4.2 获取层级结构 Deriving the Hierarchies
• 5. 实验 Experiments
• 6. 结果与讨论 Result and Discussion
• • 6.1 层级结构的比较 Comparison of the Hierarchies
  • 6.2 空间的比较 Comparison of the Spaces
  • 6.3 误差分析 Error analysis
  • 6.4 案例分析: OntoNotes
• 7. 相关工作 Related Work
• 8. 结论 Conclusions

摘要 Abstract

1. 问题: 如何在大量类别的实体中来表示有层次的信息, 从而进行实体类型识别
2. 本文研究双曲线嵌入在共享向量空间中, 捕获上下文中的实体与对应的目标类别间有层次的关系的能力
3. 本文在两个数据集上验证并调研两种用于创造大量有层次的实体类型数据的技术:

• 一种是通过专家生成的本体论(expert-generated ontology)???
• 一种是通过自动化挖掘类型的co-occurances网络???

4. 本文发现双曲线模型能够在一些情况下相对欧式方法能有所提升
5. 这种几何方法的完全度取决于类型库的颗粒度以及层次关系确定所参照的方法

1. 引入 Introduction

1. 细颗粒度的实体类型分类对于关系挖掘, 问答系统的设计等领域具有重要意义
2. 但是实体分类数量过多会导致很难挖掘实体间的内在联系, 一种解决方案是对大量的实体进行层次分级, 如person–politician–diplomat就是一条层级分类, 这样就可以实现知识的传递
3. 前人通过使用层级感知(hierarchy-aware)损失函数来构建层级实体类别信息, 或者在欧式空间中表示单词和类别的词向量表示

• 事实上不可能在欧氏空间中进行任意嵌入
• 此时我们提出双曲线嵌入, 因为双曲线是成指数增长的, 就像层级结构随层数增加是成指数增长的

4. 双曲线嵌入的下游任务是很困难的:

• 双曲线嵌入很难应用到神经模型中, 因为此时优化方法都要在双曲线空间中进行
• 目前这些问题在学术上仍然不是很清晰

5. 本文的工作:

• 在双曲线空间中构建一个细颗粒度的实体类别模型, 它同时编码了entity types和entity
• 比较两个不同的实体类别层级结构在数据集上的完全度:
  • 一个是由专家生成(WordNet)
  • 另一个是自动化生成
• 比较欧式几何和双曲线在实体类别模型, 发现双曲线的效果在超细精度的类别上表现得更好

关于双曲线嵌入在层级分类上的说明https://zhuanlan.zhihu.com/p/68104722
hyperbolic space: 对于hyperbolic space而已, 一个有限的regular tree是可以通过二维双曲空间完全表示的, 即设 r为点距中心的距离, 当$r=l$时, 认为该点对应着l所对应点等级; 而$r<l$时, 认为该点是更高等级的点; 反之更低; 双曲空间中的ball的周长与面积的计算分别是arsin和arcos都是呈指数上升的, 因此适合我们的模型;

2. 背景: 庞加莱嵌入 Background: Poincare Embeddings

1. 双曲几何是非欧空间中一类的负曲率空间
2. 二维双曲线空间可以用单位圆盘(open unit disk)表示, 即所谓庞加莱圆盘(Poincare disk)
3. 推广到多维空间圆盘模型就升级成庞加莱球

• 庞加莱球: $x\in R^n|||x||<1$ 其中$||x||$是欧式距离
• u,v两点距离: $d_H(u,v)=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}(1+\frac{2||u-v|{|}^2}{(1-||u|{|}^2)(1-||v|{|}^2)})$
  • 性质1: 若x,y接近圆盘的边缘, 即$||x||,||y||\to 1$, 则$d_H(u,v)\to d_H(x,O)+d_H(y,O)$这种性质可以视为树状层级结构里连续的指针, 即兄弟结点间的最短距离是以父节点为中介的
  • 性质2: $x$,$y$的距离随$x$,$y$的远离原点移动呈指数级增长, 与节点数随树深增长呈指数级增长类似
• 因此双曲空间是树状及层级结构的一种很合理的表征
  • 树根位于庞加莱球的原点, 下位节点接近无穷远
  • 拥有同一父节点的节点距离相对接近
  • 由此引出的庞加莱嵌入, 它的范数即表示树深, 距离即表示相似度
  • Figure2是对WordNet中的名词层级架构在二维欧氏空间与庞加莱圆盘中的表现情况
    

3. 双曲空间中的实体类别 Entity Typing in Hyperbolic Space

3.1 任务定义 Task Definition

1. 给定一个提及实体$m$的上下文句子$c$, 预测该实体的类别标签$t_m$, 其中$t_m\in T$, $T$为所有的类型集合, 目前有超过10000种不同的类型, $m$可以是命名实体, 名词或代词
2. 特别地, $t_m$可以是多标签的, 这是一个多标签分类问题

3.2 目标 Objective

1. 本文目的是分析双曲空间与欧氏空间在建模层级结构信息的效果
2. 猜想双曲空间要比欧氏空间表现得好得多
3. 为了确定度量空间(metric space)与层级结构的关系, 本文提出一个回归模型来检验
4. 本文学习了一个用于将实体与它所在的上下文映射成向量空间的方法, 因此实体将被嵌入得更接近他们的目标类别
5. 目前用于超细颗粒京都的数据集的先进模型也只能达到不足40%的精确度
6. 因此本文的验证仍然是知识性的典型实体, 能够让读者对于不同度量空间下层级结构的嵌入有更好的感知

3.3 方法 Method

1. 给定上下文$c$与实体$m$, 记为$e(m,c)\in R^{n^{\prime }}$

2. 目标学习映射函数$f:R^{n^{\prime }}\to S^n$其中$S^n$是目标向量空间

3. Figure3是模型的可视化介绍
   

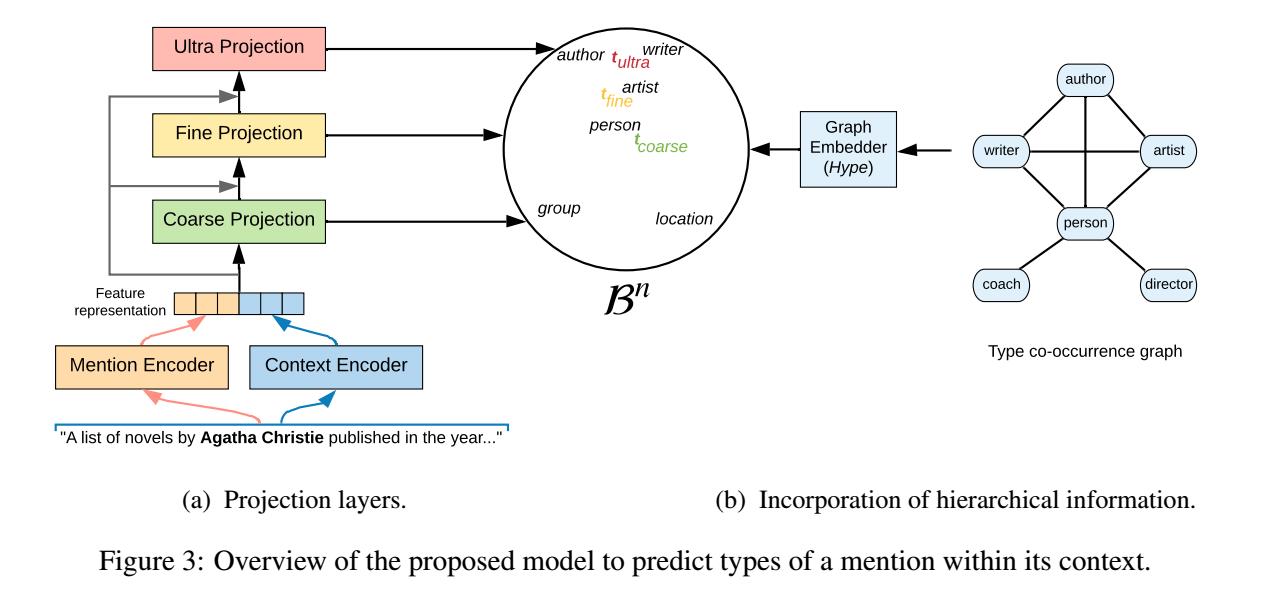
4. 由图可知类别被分为三种级别, 由粗到细分别为coarse, fine, ultra-fine, 对于三种不同级别的类别我们给出不同的映射函数$f_{coarse},f_{fine},f_{ultra}$

5. 显然随着类别变细, 映射函数的难度会更大, 因此coarse级别的映射位于模型的底层, 而ultra-fine级别的映射位于模型顶层

• 层与层之间引入归纳性的偏差, 用于指导映射到的目标区域
• 此外我们使用了残差网络中的捷径连接, 因此顶层可以直接访问编码层的向量表示

3.4 实体与上下文表示 Mention and Context Representations

1. 本文对于上下文$c$与实体$m$的编码主要基于前人的研究, 并使用单词位置嵌入$p_i$取代了位置嵌入, 用于表示第i个单词与实体间的相对位置距离; 该变动可以归纳出注意力层的偏差, 使得较少的注意力在实体上, 更多的注意力在上下文中, 最后本文在顶层采用标准的双向LSTM与自注意力编码器从而获得上下文的特征表示$C\in R^{d_c}$
2. 本文使用一个字符级别的CNN来获得实体的特征表示, 然后再与GloVe词向量拼接, 得到$M\in R^{d_m}$, 最终的模型输入为$[M;C]\in R^{d_m+d_c}$

3.5 映射到球 Projection into the Ball

1. 将实体与上下文特征表示映射到目标空间, 使用一种重参数化的变体技术

• 计算一个方向向量r与一个范数λ, 详见equation(2)
• 注意这种嵌入到庞加莱球中的方法不需要校正梯度或使用SGD优化, 但是可以用深度学习中如adam的优化方法来进行学习
  

3.6 模型优化 Optimization of the Model

1. 模型优化的目标是让映射函数$f_i$的结果接近相应的目标类别的向量, 在给定的目标类别向量空间$S^n$, 我们比较在庞加莱球$B^n$与欧式单位球$R^n$上的表现
2. $B^n$与$R^n$都是度量空间, 因此都有距离函数分别为$d_H$与$d_E$, 这是用于最小化的损失函数
3. 此外庞加莱模型是双曲空间中具有保角性质的模型, 即欧式与双曲空间中的角是相等的, 余弦距离也同样可以使用
4. 事实上最小化的是距离的线性组合, 因为这种距离不符合柯西施瓦兹不等式, 因此不是一种传统的距离度量, 但是它
5. 为了缓和双曲距离的不稳定性(y趋于x时, x,y的双曲距离偏导x趋于无穷), 我们引入前人的方法:

• 庞加莱球中的距离之所以要平方是因为不平方的话在$B^n$没有连续的导数
• 超参数$\alpha$与$\beta$是对余弦距离函数的图像边缘的在区间[0,1]补偿(原文: The hyperparameters $\alpha$ and $\beta$ are added to compensate the bounded image of the cosine distance function in [0,1])
  d B ( u , v ) = α ( d H ( u , v ) ) 2

  以上是关于论文阅读基于层级关系的词向量：双曲空间词嵌入的主要内容，如果未能解决你的问题，请参考以下文章

  句子编码和语境化词嵌入有啥区别？

  通俗讲解pytorch中nn.Embedding原理及使用

  机器人--寒暄库

  机器人--寒暄模型

  二、词向量和语义

  论文阅读 A SIMPLE BUT TOUGH-TO-BEAT BASELINE FOR SEN- TENCE EMBEDDINGS