读取GPS星历文件读取GPS的星历文件,并动态显示卫星移动效果
Posted fpga&matlab
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了读取GPS星历文件读取GPS的星历文件,并动态显示卫星移动效果相关的知识,希望对你有一定的参考价值。
1.软件版本
matlab2013b
2.本算法理论知识
GPS卫星轨道周期几乎是24小时,而自己的卫星在太阳同步轨道上的周期大概是1.5个小时,那么就是说太阳同步轨道已经绕几周了,GPS卫星才饶一周。所以当算多普勒频移的时候只需要算出GPS一个周期时间内的多普勒频移就好了。就是说,如果在算多普勒频移的时候,如果算多过24小时,那么多普勒频移就会重复了。我只需要24小时GPS轨道周期内的多普勒频移就好了。
这里,首先介绍一下星历文件的含义:
| Prn | 卫星编号 |
| iode | 电文中给出的当前参考历元的有效期 |
| Crs | 电文中给出的轨道半径角距的改正项—正弦振幅 |
| delta_n | 电文中给出的平地点角改正值 |
| M_zero | 电文中给出的参考时刻平近点角 |
| Cuc | 电文中给出的升交点赤经的改正项—余弦振幅 |
| e1 | 电文中给出的轨道椭圆偏心率 |
| Cus | 电文中给出的升交点赤经的改正项—正弦振幅 |
| sqrt_a | 电文中给出的卫星轨道椭圆长半轴的平方根 |
| toe | 电文中给出的参考时刻 |
| Cic | 电文中给出的倾角角距的改正项—余弦振幅 |
| OMEGA_zero | 电文中给出的参考时刻升交点赤经 |
| Cis | 电文中给出的倾角角距的改正项—正弦振幅 |
| i_zero | 电文中给出的参考时刻轨道倾角 |
| Crc | 电文中给出的轨道半径角距的改正项—余弦振幅 |
| omega | 电文中给出的轨道近地点角距 |
| OMEGA_dot | 电文中给出的升交点赤经变化率 |
| i_dot | 电文中给出的轨道倾角变化率 |
这里需要注意的时候,由于GPS距离地面的高度一般为20000km,而这里的同步卫星只有350km,所以看上去会效果不明显,所以这里我们把这里的参数设置的大些,这样看上去效果稍微明显点。然后你再写论文的时候,如果用到其中的数据,只要把他改回350即可。另外,其周期为1.5小时,这样在房子的时候,速度太快,不容易观察,这里稍微设置的大些,使用周期为6小时。
3.部分源码
clc;
clear;
close all;
warning off;
addpath 'func\\'
%读取星历文件
NavData = func_ReadNavFile('file.02n');
%参数初始化
Gravitational_constant = 3986005e+8; %引力常数
Earth_rotation_angular_velocity = 7.2921151467e-5; %地球自转角速度
%显示卫星标号
Prns = [1:24];
%卫星信号发射时刻
SIZE = size(NavData);
EphemerisNum = SIZE(1);
startTime = (NavData(EphemerisNum,19)+NavData(1,19))/2 - 21600;
%时间量,以10分钟为间隔,共144个点
Days = 144;
%定义6个轨道面
GDNUM = 6;
%速度变量
Vx_GPS = zeros(length(Prns),Days);
Vy_GPS = zeros(length(Prns),Days);
Vz_GPS = zeros(length(Prns),Days);
%位置变量
Px_GPS = zeros(length(Prns),Days);
Py_GPS = zeros(length(Prns),Days);
Pz_GPS = zeros(length(Prns),Days);
%频偏变量
Fx_GPS = zeros(length(Prns),Days);
Fy_GPS = zeros(length(Prns),Days);
Fz_GPS = zeros(length(Prns),Days);
%速度变量
Vx_SAT = zeros(length(Prns),Days);
Vy_SAT = zeros(length(Prns),Days);
Vz_SAT = zeros(length(Prns),Days);
%位置变量
Px_SAT = zeros(length(Prns),Days);
Py_SAT = zeros(length(Prns),Days);
Pz_SAT = zeros(length(Prns),Days);
%一个轨道周期
E = [0:2*pi/Days:2*pi];
Height = 20000e3;
%一个轨道周期2
Cycle = 6;
E2 = [0:24/Cycle*2*pi/Days:24/Cycle*2*pi];
Height1 = 7000e3;
Height2 = 14000e3;
%解析读取的星历文件
for i = 1:length(Prns)
for j = 1:Days
t = startTime + j*600;
x = Height*cos(E(j));
y = Height*sin(E(j));
z = 0;
%根据时间选择历元
%根据时间选择历元
min = 604800;
for k= 1:EphemerisNum
Prn = NavData(k,1);
toe = NavData(k,19);
if (Prn == Prns(i))
if (abs(t-toe) < min)
min = abs(t-toe);
PRNS_SEL = k;
end
end
end
%计算GPS卫星轨道
%计算GPS卫星轨道
Prn = NavData(PRNS_SEL,1);
%电文中给出的当前参考历元的有效期
iode = NavData(PRNS_SEL,11);
%电文中给出的轨道半径角距的改正项—正弦振幅
Crs = NavData(PRNS_SEL,12);
%电文中给出的平地点角改正值
delta_n = NavData(PRNS_SEL,13);
%电文中给出的参考时刻平近点角
M_zero = NavData(PRNS_SEL,14);
%电文中给出的升交点赤经的改正项—余弦振幅
Cuc = NavData(PRNS_SEL,15);
%电文中给出的轨道椭圆偏心率
es = NavData(PRNS_SEL,16);
%电文中给出的升交点赤经的改正项—正弦振幅
Cus = NavData(PRNS_SEL,17);
%电文中给出的卫星轨道椭圆长半轴的平方根
sqrt_a = NavData(PRNS_SEL,18);
%电文中给出的参考时刻(周积秒)
toe = NavData(PRNS_SEL,19);
%电文中给出的倾角角距的改正项—余弦振幅
Cic = NavData(PRNS_SEL,20);
%电文中给出的参考时刻升交点赤经
OMEGA_zero = NavData(PRNS_SEL,21);
%电文中给出的倾角角距的改正项—正弦振幅
Cis = NavData(PRNS_SEL,22);
%电文中给出的参考时刻轨道倾角
i_zero = NavData(PRNS_SEL,23);
%电文中给出的轨道半径角距的改正项—余弦振幅
Crc = NavData(PRNS_SEL,24);
%电文中给出的轨道近地点角距
omega = NavData(PRNS_SEL,25);
%电文中给出的升交点赤经变化率
OMEGA_dot = NavData(PRNS_SEL,26);
%电文中给出的轨道倾角变化率
i_dot = NavData(PRNS_SEL,27);
%计算观测时刻GPS卫星的坐标
%计算观测时刻GPS卫星的坐标
n_initial = sqrt(Gravitational_constant)/(sqrt_a*sqrt_a*sqrt_a);
%计算平均角速度
n = n_initial + delta_n;
%计算观测时刻到参考时刻的规化时间
t_k = func_tk_limits(t,toe);
%观测时刻的卫星平近点角
M_k = M_zero + n * t_k + 2*pi;
E_k = M_k;
E_k1= M_k - es*sin(E_k);
%计算观测时刻的偏近点角
while (abs(E_k - E_k1) > 1e-9)
E_k1 = E_k;
E_k = M_k + es * sin(E_k1);
end;
%计算真近点角
v_k = 2*atan(sqrt((1+es)/(1-es))*tan(E_k/2));
%计算升交距角
phi_k = v_k + omega;
%计算摄动校正项
C_u = Cus*sin(2*phi_k) + Cuc*cos(2*phi_k);
C_r = Crs*sin(2*phi_k) + Crc*cos(2*phi_k);
C_i = Cis*sin(2*phi_k) + Cic*cos(2*phi_k);
%计算摄动校正后的升交距角、卫星矢径、轨道倾角
u_k = phi_k + C_u;
r_k = sqrt_a*sqrt_a*(1-es*cos(E_k)) + C_r;
i_k = i_zero + i_dot*t_k + C_i;
%计算卫星在轨道坐标系中的位置
x_k = r_k * cos(u_k);
y_k = r_k * sin(u_k);
%计算观测时刻卫星的升交点经度
OMEGA_k = OMEGA_zero + (OMEGA_dot-Earth_rotation_angular_velocity)*t_k - Earth_rotation_angular_velocity*toe;
%计算卫星在平面坐标系中的位置
X_k = x_k*cos(OMEGA_k) - y_k*cos(i_k)*sin(OMEGA_k);
Y_k = x_k*sin(OMEGA_k) + y_k*cos(i_k)*cos(OMEGA_k);
Z_k = y_k*sin(i_k);
%实际空间轨道坐标
A1=[32.8,92.8,152.8,212.8,272.8,332.8];
for k=1:GDNUM
A(k) = A1(k)*pi/180;
B(k) = 55*pi/180;
C(k) = pi/100;
R1= [1 0 0;
0 cos(B(k)) -sin(B(k));
0 sin(B(k)) cos(B(k))];
R2= [cos(C(k)) -sin(C(k)) 0;
sin(C(k)) cos(C(k)) 0;
0 0 1];
R3= [cos(A(k)) -sin(A(k)) 0;
sin(A(k)) cos(A(k)) 0;
0 0 1];
R312 = R3*R1*R2;
Ans = R312*[x;y;z];
x1(k,j) = Ans(1,:);
y1(k,j) = Ans(2,:);
z1(k,j) = Ans(3,:);
end
%计算信号发射时刻的E_k_dot
M_k_dot = n;
E_k_dot = M_k_dot/[1 - es*cos(E_k)];
%计算信号发射时刻的phi_k_dot
v_k_dot = sqrt(1-es*es)*E_k_dot/(1-es*cos(E_k));
phi_k_dot = v_k_dot;
C_i_dot = 2*phi_k_dot*(Cis*cos(2*phi_k)-Cic*sin(2*phi_k));
C_r_dot = 2*phi_k_dot*(Crs*cos(2*phi_k)-Crc*sin(2*phi_k));
C_u_dot = 2*phi_k_dot*(Cus*cos(2*phi_k)-Cuc*sin(2*phi_k));
%计算发射时刻的C_u_dot,C_i_dot,C_r_dot
u_k_dot = phi_k_dot + C_u_dot;
r_k_dot = sqrt_a*sqrt_a*es*E_k_dot*sin(E_k) + C_r_dot;
i_k_dot = i_dot + C_i_dot;
OMEGA_k_dot = OMEGA_dot - Earth_rotation_angular_velocity;
%计算信号发射时刻的u_k_dot,r_k_dot,i_k_dot,OMEGA_k_dot
x_k_dot = r_k_dot*cos(u_k) - r_k*u_k_dot*sin(u_k);
y_k_dot = r_k_dot*sin(u_k) + r_k*u_k_dot*cos(u_k);
%计算信号发射时刻卫星在轨道平面直角坐标系中的速度
X_k_dot = x_k_dot*cos(OMEGA_k) - Y_k*OMEGA_k_dot - (y_k_dot*cos(i_k)-Z_k*i_k_dot)*sin(OMEGA_k);
Y_k_dot = x_k_dot*sin(OMEGA_k) + X_k*OMEGA_k_dot + (y_k_dot*cos(i_k)-Z_k*i_k_dot)*cos(OMEGA_k);
Z_k_dot = y_k_dot*sin(i_k) + y_k*i_k_dot*cos(i_k);
%速度变量
Vx_GPS(i,j) = X_k_dot;
Vy_GPS(i,j) = Y_k_dot;
Vz_GPS(i,j) = Z_k_dot;
%位置变量
Px_GPS(i,j) = X_k;
Py_GPS(i,j) = Y_k;
Pz_GPS(i,j) = Z_k;
%人工模拟自己的太阳轨道同步卫星
Px_MY(j) = (Height1+6300e3)*cos(E2(j))*cos(pi*(98-90)/180);
Py_MY(j) = (Height2+6300e3)*sin(E2(j));
Pz_MY(j) = (Height1+6300e3)*cos(E2(j))*sin(pi*(98-90)/180);
%计算每个时刻的频偏
%计算每个时刻的频偏
if j == 1
Fx_GPS(i,j) = 0;
Fy_GPS(i,j) = 0;
Fz_GPS(i,j) = 0;
else
Fx_GPS(i,j) = 1575.42e6/3e8*abs(Vx_GPS(i,j)-Vx_GPS(i,j-1));
Fy_GPS(i,j) = 1575.42e6/3e8*abs(Vy_GPS(i,j)-Vy_GPS(i,j-1));
Fz_GPS(i,j) = 1575.42e6/3e8*abs(Vz_GPS(i,j)-Vz_GPS(i,j-1));
end
end
end
for i = 1:24
for j = 1:144
Frei(j,:) = [Fx_GPS(i,j), Fy_GPS(i,j), Fz_GPS(i,j)];
end
end
%显示卫星轨迹,动态显示
%显示卫星轨迹,动态显示
L = length(x1);
X1 = x1;
Y1 = y1;
Z1 = z1;
X2 = [x1(:,round(1*L/4)+1:end),x1(:,1:round(1*L/4))];
Y2 = [y1(:,round(1*L/4)+1:end),y1(:,1:round(1*L/4))];
Z2 = [z1(:,round(1*L/4)+1:end),z1(:,1:round(1*L/4))];
X3 = [x1(:,round(2*L/4)+1:end),x1(:,1:round(2*L/4))];
Y3 = [y1(:,round(2*L/4)+1:end),y1(:,1:round(2*L/4))];
Z3 = [z1(:,round(2*L/4)+1:end),z1(:,1:round(2*L/4))];
X4 = [x1(:,round(3*L/4)+1:end),x1(:,1:round(3*L/4))];
Y4 = [y1(:,round(3*L/4)+1:end),y1(:,1:round(3*L/4))];
Z4 = [z1(:,round(3*L/4)+1:end),z1(:,1:round(3*L/4))];
colortable;
figure;
%根据计算得到的速度,模拟动态的卫星运动效果
for time = 1:Days
for i=1:GDNUM
plot3(x1(i,:),y1(i,:),z1(i,:),colorsi);
hold on
plot3(X1(i,time),Y1(i,time),Z1(i,time),colors1i);
hold on
plot3(X2(i,time),Y2(i,time),Z2(i,time),colors2i);
hold on
plot3(X3(i,time),Y3(i,time),Z3(i,time),colors3i);
hold on
plot3(X4(i,time),Y4(i,time),Z4(i,time),colors4i);
hold on
end
plot3(Px_MY(:),Py_MY(:),Pz_MY(:),'r','linewidth',2);
hold on
plot3(Px_MY(time),Py_MY(time),Pz_MY(time),'--rs','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g','MarkerSize',5);
hold on
func_earth();
pause(0.01);
axis([-30e6,30e6,-30e6,30e6,-30e6,30e6]);
xlabel('X');
xlabel('Y');
xlabel('Z');
title('GPS卫星动态模拟效果');
grid on;
hold off;
end
%计算各个时刻各个卫星的频移,并以表格形式输出
%计算各个时刻各个卫星的频移,并以表格形式输出
4.仿真分析
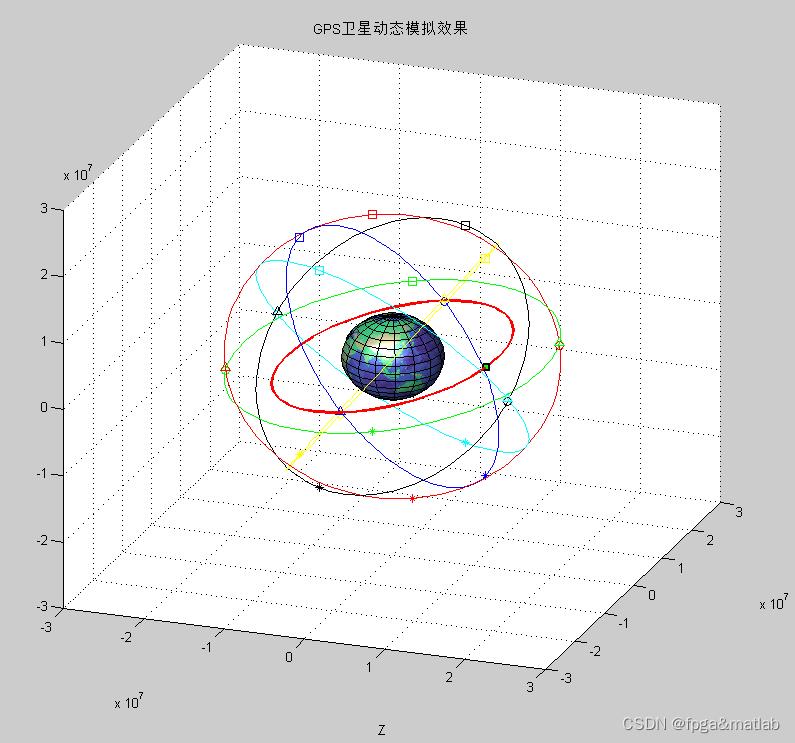
5.参考文献
[1]张妮, 王标标. 基于Matlab读取标准RINEX格式的GPS星历数据[J]. 电子设计工程, 2010, 18(8):3.A01-82
以上是关于读取GPS星历文件读取GPS的星历文件,并动态显示卫星移动效果的主要内容,如果未能解决你的问题,请参考以下文章