边长为6，7，8的三角形最大角与最小角的和是多少？

Posted 2023-03-21

结果为：120度

解题过程如下（因有度数和角符号无法编辑，故只能截图）：

扩展资料

诱导公式：

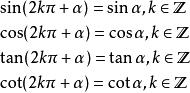
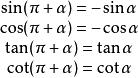
三角函数性质：

在直角三角形中，当平面上的三点A、B、C的连线，AB、AC、BC，构成一个直角三角形，其中角ACB为直角。对角BAC而言，对边（opposite）a=BC、斜边（hypotenuse）c=AB、邻边（adjacent）b=AC。

如果一个函数f（x）的所有周期中存在一个最小的正数，那么这个最小的正数就叫做f（x）的最小正周期（minimal positive period）。例如，正弦函数的最小正周期是2π。

对于正弦函数y=sin x，自变量x只要并且至少增加到x+2π时，函数值才能重复取得。正弦函数和余弦函数的最小正周期是2π。

参考技术A 根据大边对大角，中间的角所对边
是7
,设此角为
B
7^2
=
5^2
+
8^2
-
2
*
5
*
8
*
cosB
49
=
25
+
64
-
80cosB
cosB
=
1/2
B
=
60
则另两个角，也就是最大角与最小角之和=
120

边长为5、7、8的三角形的最大角与最小角之和是多少

请写出解题步骤，说明这类题应怎样做，谢谢

结果为：120度

解题过程如下（因有度数和角符号无法编辑，故只能截图）：

扩展资料

诱导公式：

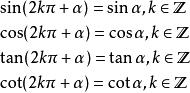
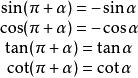
三角函数性质：

在直角三角形中，当平面上的三点A、B、C的连线，AB、AC、BC，构成一个直角三角形，其中角ACB为直角。对角BAC而言，对边（opposite）a=BC、斜边（hypotenuse）c=AB、邻边（adjacent）b=AC。

如果一个函数f（x）的所有周期中存在一个最小的正数，那么这个最小的正数就叫做f（x）的最小正周期（minimal positive period）。例如，正弦函数的最小正周期是2π。

对于正弦函数y=sin x，自变量x只要并且至少增加到x+2π时，函数值才能重复取得。正弦函数和余弦函数的最小正周期是2π。

参考技术A 用余弦公式
解：设三角形ABC中 a=5 b=7 c=8
则锐角三角形中最大角与最小角为C和A
b方=a方+c方-2ac*cosB
解得cosB=1/2
B=60度
A+C=120度本回答被提问者采纳 参考技术B 由余弦定理可以知道边长7对应角为60度,所以最大角和最小角之和,也就是5和8所对应的2个角之和为180-60=120度 参考技术C 可以设定5,7,8对应的角为:A,C,B
cos(A+B)=cosAcosB-sinAsinB
有余璇定理得:cosα=(B^2+C^2-A^2)/2BC
COSA=11/14
COSB=1/7
然后求出SINA SINB
带入cos(A+B)=cosAcosB-sinAsinB
得cos(A+B)=-0.5
因为0<A+B<180
所以A+B=120 参考技术D 余弦定理吧
角最大就是余弦值最小
反之

所以不难求出