数据结构与算法: 使用栈解决计算器问题

Posted 2022-05-12 android超级兵

数据结构与算法:使用栈解决计算器问题

Tips: 采用java语言, 关注博主,底部附有完整代码

使用到的知识点:

• 栈
• 中后缀表达式
• 后缀表达式
• 中缀表达式转后缀表达式

支持范围: + - * / 小括号() 小数点

例如: 
案例一: 20 - 5 + 25 / 5 + 20 / 5 + 100 - 24 - 0.4
案例二: (3 + 5 + 2.5) - 2 * 5 

效果图

案例一	案例二

案例二思路分析图:

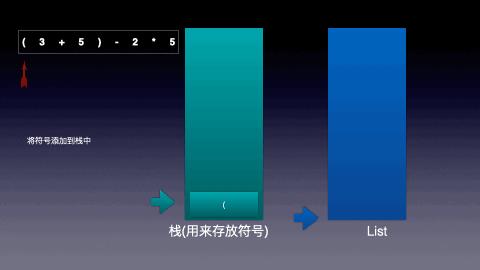
案例一(不带括号)

注释我写的很详细,直接看完整代码:

/**
 * @author: android 超级兵
 * @create: 2022-05-07 11:08
 * TODO 使用栈来解决计算器计算问题
 **/
public class Client 
    public static void main(String[] args) 

        // 结果 = 100
        String str = "20-5+25/5+20/5+100-24-0.4";
        // 用来存放数字
        CalculatorStack numberStack = new CalculatorStack(str.length());
        // 用来存放符号
        CalculatorStack operatorStack = new CalculatorStack(str.length());

        // 解析公式
        List<String> parse = parseInfixFormula(str);

        // 循环每一次 合理的入栈
        for (String value : parse) 
            if (value == null) 
                continue;
            

            // 判断是否是数字
            if (isNumber(value)) 
                // 数字
                numberStack.push(Float.parseFloat(value));
             else 
                // 符号

                char operator = value.charAt(0);
//                System.out.println("符号:" + operator);

                // 判断符号栈是否为null
                if (operatorStack.isEmpty()) 
                    // 符号第一次加载的时候 直接添加进去
                    operatorStack.push(operator);
                 else 
                    // 不是第一次加载

                    // 先判断优先级
                    if (getLevel(operator) < getLevel((char) operatorStack.seeHeadData())) 
                        // 如果当前优先级 < 顶部的优先级
                        // 例如 即将添加的符号为 + , 顶部的符号为 *
                        // 那么先取出数栈中2个数，和符号栈中一个数 计算
                        // 最终将计算结果在添加到数栈中...

                        float num1 = numberStack.pop();
                        float num2 = numberStack.pop();
                        char oper = (char) operatorStack.pop();
                        float result = result(num1, num2, oper);
                        System.out.printf("先计算:%.1f %c %.1f = %.1f\\n", num2, oper, num1, result);
                        numberStack.push(result);
                        operatorStack.push(operator);
                     else 
                        // 如果优先级相等 则直接加入
                        operatorStack.push(operator);
                    
                
            
        

        // 反转数据！
        numberStack.reverse();
        operatorStack.reverse();

        // 计算最终结果
        while (!operatorStack.isEmpty()) 
            float num1 = numberStack.pop();
            float num2 = numberStack.pop();
            char operator = (char) operatorStack.pop();
            float result = result(num2, num1, operator);
            System.out.printf("计算:%.1f %c %.1f = %.1f\\n", num1, operator, num2, result);
            numberStack.push(result);
        

        System.out.println("最终结果为:" + str + " = " + numberStack.seeHeadData());
    

使用数组模拟栈

/**
 * @author: android 超级兵
 * @create: 2022-05-07 11:10
 **/
public class CalculatorStack 

    // 用来存放数据
    float[] mStacks;

    // top的坐标
    int currentIndex = -1;

    /**
     * @param max 栈的最大值
     */
    public CalculatorStack(int max) 
        mStacks = new float[max];
    

    public synchronized void push(float value) 
        // 判断栈是否满
        if (isFull()) 
            System.out.println("栈满了～～");
            return;
        


        currentIndex++;
        mStacks[currentIndex] = value;
    

    // 懒的判断是否为null了
    public float seeHeadData() 
        try 
            return mStacks[currentIndex];
         catch (Exception e) 
            return 0;
        
    

    // 弹出
    public synchronized float pop() 
        if (isEmpty()) 
            throw new NullPointerException("栈空了");
        
        float value = mStacks[currentIndex];
        mStacks[currentIndex] = 0;
        currentIndex--;
        return value;
    

    public synchronized void show() 
        for (int i = mStacks.length - 1; i >= 0; i--) 
            if (mStacks[i] != 0) 
                System.out.println(mStacks[i]);
            
        
        System.out.println();
    

    public void showChar() 
        for (int i = mStacks.length - 1; i >= 0; i--) 
            if (mStacks[i] != 0) 
                System.out.println((char) mStacks[i]);
            
        
        System.out.println();
    

    /*
     * @author: android 超级兵
     * @create: 2022/5/7 18:09
     * TODO 反转数据
     */
    public synchronized void reverse() 
        float[] tempInts = new float[mStacks.length];

        int index = 0;
        while (!isEmpty()) 
            tempInts[index++] = pop();
        

        for (float value : tempInts) 
            if (value != 0) 
                push(value);
            
        
    

    /*
     * @author: android 超级兵
     * @create: 2022/5/7 11:15
     * TODO 是否栈满
     */
    public boolean isFull() 
        return currentIndex == mStacks.length;
    

    /*
     * @author: android 超级兵
     * @create: 2022/5/7 11:15
     * TODO 是否栈空
     */
    public boolean isEmpty() 
        return currentIndex == -1;
    

运行结果:

先计算:25.0 / 5.0 = 5.0
先计算:20.0 / 5.0 = 4.0
计算:20.0 - 5.0 = 15.0
计算:15.0 + 5.0 = 20.0
计算:20.0 + 4.0 = 24.0
计算:24.0 + 100.0 = 124.0
计算:124.0 - 24.0 = 100.0
计算:100.0 - 0.4 = 99.6
最终结果为:20-5+25/5+20/5+100-24-0.4 = 99.6

案例二(带括号)

/**
 * @author: android 超级兵
 * @create: 2022-05-09 00:43
 * TODO 解决计算器中带有括号的优先级
 * 例如: 中缀表达式: ( 3 + 4 ) * 5 - 6 = 29
 * 后缀表达式:  3 4 + 5 * 6 -
 **/
public class Client 
    public static void main(String[] args) 

//        后缀
//        String formula = "3 4 + 5 * 6 -";
//        // 解析后缀表达式
//        List<String> str = FormulaUtil.parseSuffixFormula(formula);

        // 中缀
        String formula = "(3 + 5 + 2.5) - 2 * 5";
        // 中缀 转 后缀
        List<String> str = FormulaUtil.inFixToSuffix(formula);

        Stack<String> numberStack = new Stack<>();

        for (String item : str) 
            if (FormulaUtil.isNumber(item)) 
                // 数字
//                System.out.println("数字:" + item);
                // 数字直接入栈
                numberStack.push(item);
             else 
                // 符号
//                System.out.println("符号:" + item);
                float number1 = Float.parseFloat(numberStack.pop());
                float number2 = Float.parseFloat(numberStack.pop());
                char oper = item.charAt(0);
                float res = FormulaUtil.result(number1, number2, oper);
                System.out.printf("计算:%.1f %c %.1f = %.1f\\n", number2, oper, number1, res);
                numberStack.push(String.valueOf(res));
            
        
        System.out.println("最终结果为:" + numberStack.pop());
    

FormulaUtil 辅助类

/**
 * @author: android 超级兵
 * @create: 2022-05-09 00:48
 * TODO 公式辅助类
 **/
public class FormulaUtil 

    /*
     * @author: android 超级兵
     * @create: 2022/5/9 01:21
     * TODO 中缀转后缀
     * 例如 (3 + 5) * 2 - 5 => 3 5 + 2 * 5 -
     * (4 + (8 - 5) * 3 - 5 => 4 8 5 - + 3 * 5 -
     */
    public static List<String> inFixToSuffix(String infix) 

        List<String> infixList = parseInfixFormula(infix);

        // 存放符号元素
        Stack<String> elementStack = new Stack<>();

        // 存放符号 + 数字元素
        ArrayList<String> elementList = new ArrayList<>();


        for (String item : infixList) 
            if (isNumber(item)) 
                // 数字
                elementList.add(item);
             else if (item.equals("(")) 
                elementStack.push(item);
             else if (item.equals(")")) 
                while (!elementStack.peek().equals("(")) 
                    String pop = elementStack.pop();
                    elementList.add(pop);
                
                // 弹出 )
                elementStack.pop();
             else 
                // 符号
//                System.out.println("符号为:" + item);


                if (elementStack.size() != 0 && getLevel(elementStack.peek().charAt(0)) > getLevel(item.charAt(0))) 
                    // 如果 栈顶等级 > 当前符号的等级
                    elementList.add(elementStack.pop());
                

                // 将当前符号压入栈中
                elementStack.push(item);
            
        

        // 将 elementStack 中剩余元素 添加到 elementList中
        while (elementStack.size() != 0) 
            elementList.add(elementStack.pop());
        

        System.out.println("中缀为:" + infix);
        System.out.println("中缀转后缀最终结果为:");
        for (String o : elementList) 
            System.out.println(o);
        
        return elementList;
    

    /*
     * @author: android 超级兵
     * @create: 2022/5/9 01:05
     * TODO 解析后缀表达式 例如str = "3 4 + 5 * 6 -";
     * 解析后:
     * 3
     * 4
     * +
     * 5
     * *
     * 6
     * -
     * tips: 注意后缀表达式格式，每个元素之间空格隔开!
     */
    public static List<String> parseSuffixFormula(String str) 
        return Arrays.asList(str.split(" "));
    

    /*
     * @author: android 超级兵
     * @create: 2022/5/7 15:41
     * TODO 解析中缀表达式 例如 str = "62-5+25/5";
     * 解析后:
     *  62
     *  -
     *  5
     *  +
     *  25
     *  /
     *  5
     */
    public static ArrayList<String> parseInfixFormula(String str) 
        StringBuilder temp = new StringBuilder();
        ArrayList<String> numbers = new ArrayList<>();

        // 消除所有的空格
        str = str.replaceAll(" ", "");

        for (int i = 0; i < str.length(); i++) 
            char indexValue = str.charAt(i);

            // 判断是否是符号
            if (isOperator(indexValue)) 
//                System.out.println("符号:" + indexValue);
                // 是符号
                numbers.add(String.valueOf(indexValue));
             else 
                // 是数字
//                System.out.println("数字:" + indexValue);

                int check = (int) indexValue - 48;
                // 46代表小数点
                // ASCII码对照表: https://www.habaijian.com/
                if ((check < 0 || check > 9) && indexValue != 46) 
                    throw new RuntimeException("存在特殊符号");
                

                // 是否是最后一位数字
                if (i == str.length() - 1) 
                    // 直接添加
                    numbers.add(String.valueOf(temp) + indexValue);
                 else 
                    // 如果不是符号，则一直记录
                    temp.append(indexValue);
                    // 判断下一位是否是符号
                    if (isOperator(str.charAt(i + 1))) 
                        // 符号
                        numbers.add(temp.toString());
                        // 清空stringBuilder
                        temp = new StringBuilder();
                    
                
            
        
        System.out.println("解析完成:");
        for (String number : numbers) 
            if (null != number) 
                System.out.println(number);
            
        
        System.out.println();
        return numbers;
    

    /**
     * TODO 是否是符号(+ , - , * , /)
     */
    public static boolean isOperator(char value) 
        return value == '+'
                以上是关于数据结构与算法: 使用栈解决计算器问题的主要内容，如果未能解决你的问题，请参考以下文章
 
 数据结构与算法中缀表达式转后缀表达式以及后缀表达式的计算
 基础算法与数据结构前缀中缀后缀表达式
 飞行日记之数据结构与算法分析——栈与四则运算
 中缀表达式与后缀表达式
 学习数据结构笔记=====＞栈
 数据结构-栈的应用之中缀表达式的计算