队列练习之Example001-用两个栈 s1 和 s2 来模拟一个队列,实现队列的出队入队队是否为空的运算
Posted 二木成林
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了队列练习之Example001-用两个栈 s1 和 s2 来模拟一个队列,实现队列的出队入队队是否为空的运算相关的知识,希望对你有一定的参考价值。
Example001
题目
请利用两个栈 s1 和 s2 来模拟一个队列,假设栈中元素为 int 型,栈中元素最多为 maxSize。已知栈的 3 个运算定义如下:
push(ST, x):元素 x 入 ST 栈。pop(ST, &x):ST 栈顶元素出栈,赋给变量 x。isEmpty(ST):判断 ST 栈是否为空。
如何利用栈的运算来实现该队列的 3 个运算:enQueue(元素入队列)、deQueue(元素出队列)、isQueueEmpty(判断队列是否为空,空返回 1,不空返回 0)。
分析
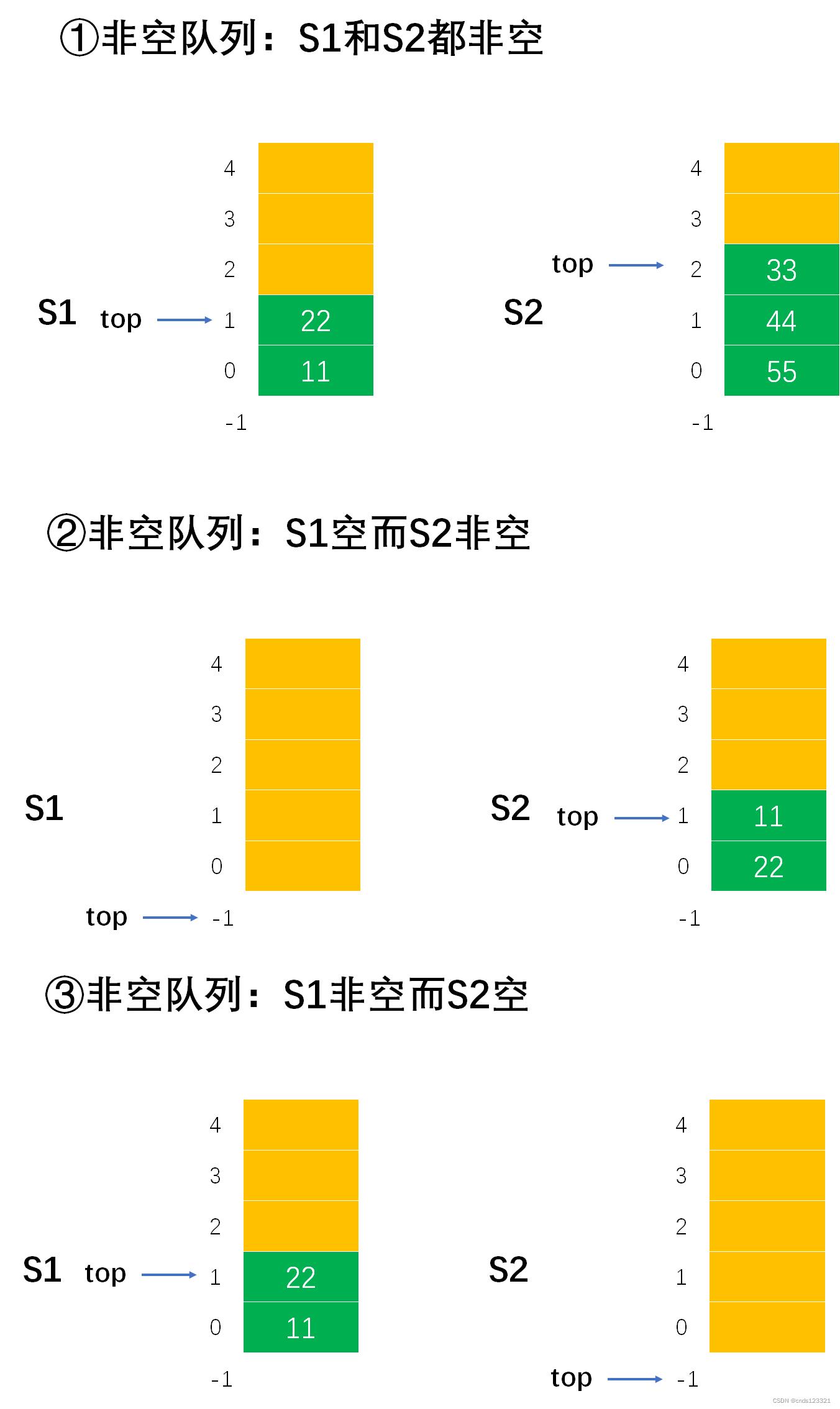
利用两个栈 S1 和 S2 来模拟一个队列,当需要向队列中插入一个元素时,用栈 S1 来存放入队的元素,即 S1 执行入栈操作。当需要出队时,则对栈 S2 执行出栈操作。由于从栈中取出元素的顺序是原顺序的逆序,所以必须先将 S1 中的所有元素全部出栈并压入到 S2 栈中,再在 S2 中执行出栈操作,即可实现出队操作,而在执行此操作前必须判断 S2 是否为空,否则会导致顺序混乱。当 S1 和 S2 都为空时队列才为空。
之前也写过这题,可以参考:考研数据结构之队列(3.3)——练习题之利用两个栈s1和s2来模拟一个队列,然后利用栈的运算来实现队列的enQueue、deQueue及isQueueEmpty运算(C表示)。
图解
- 空队列

- 非空队列
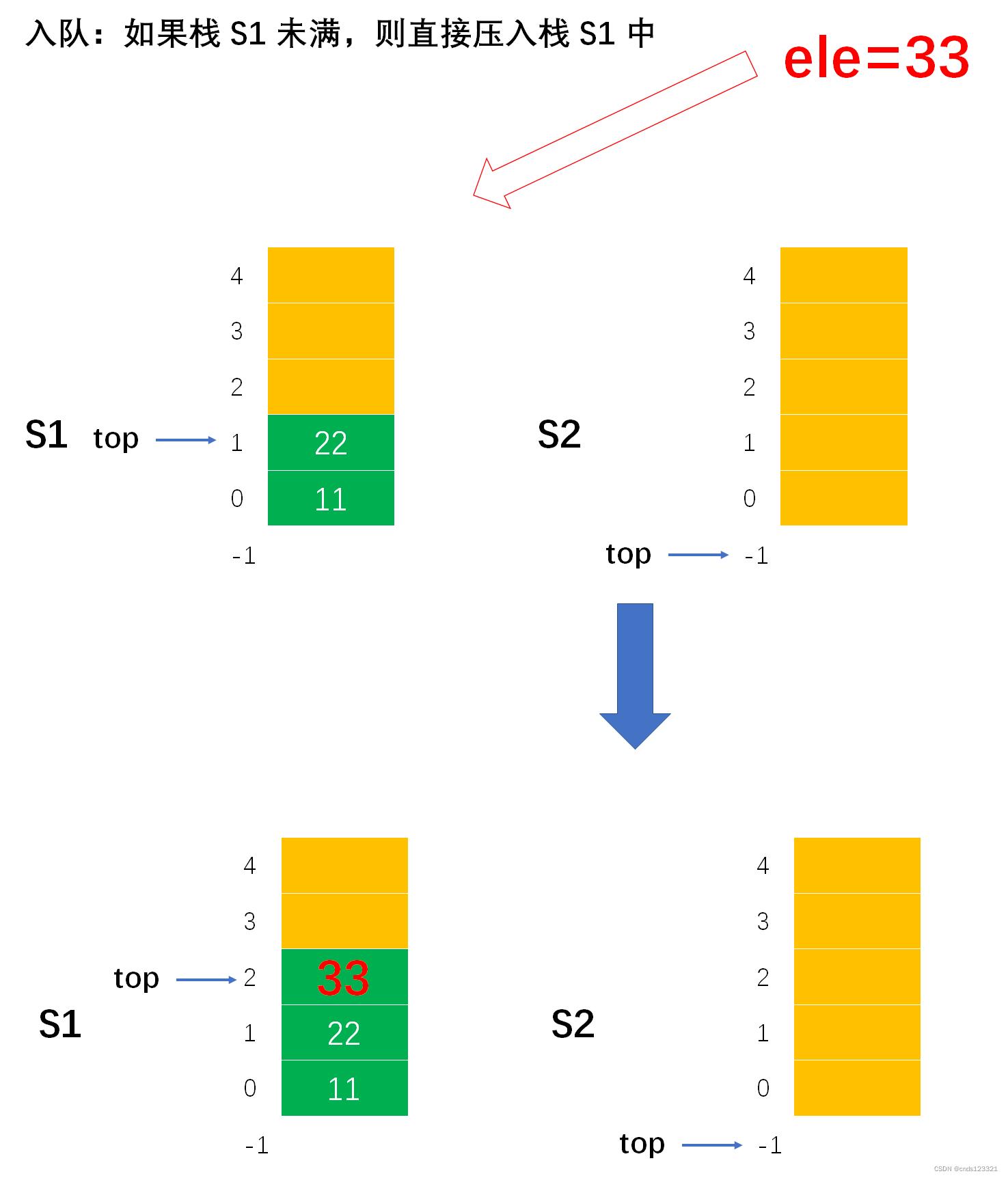
- 入队

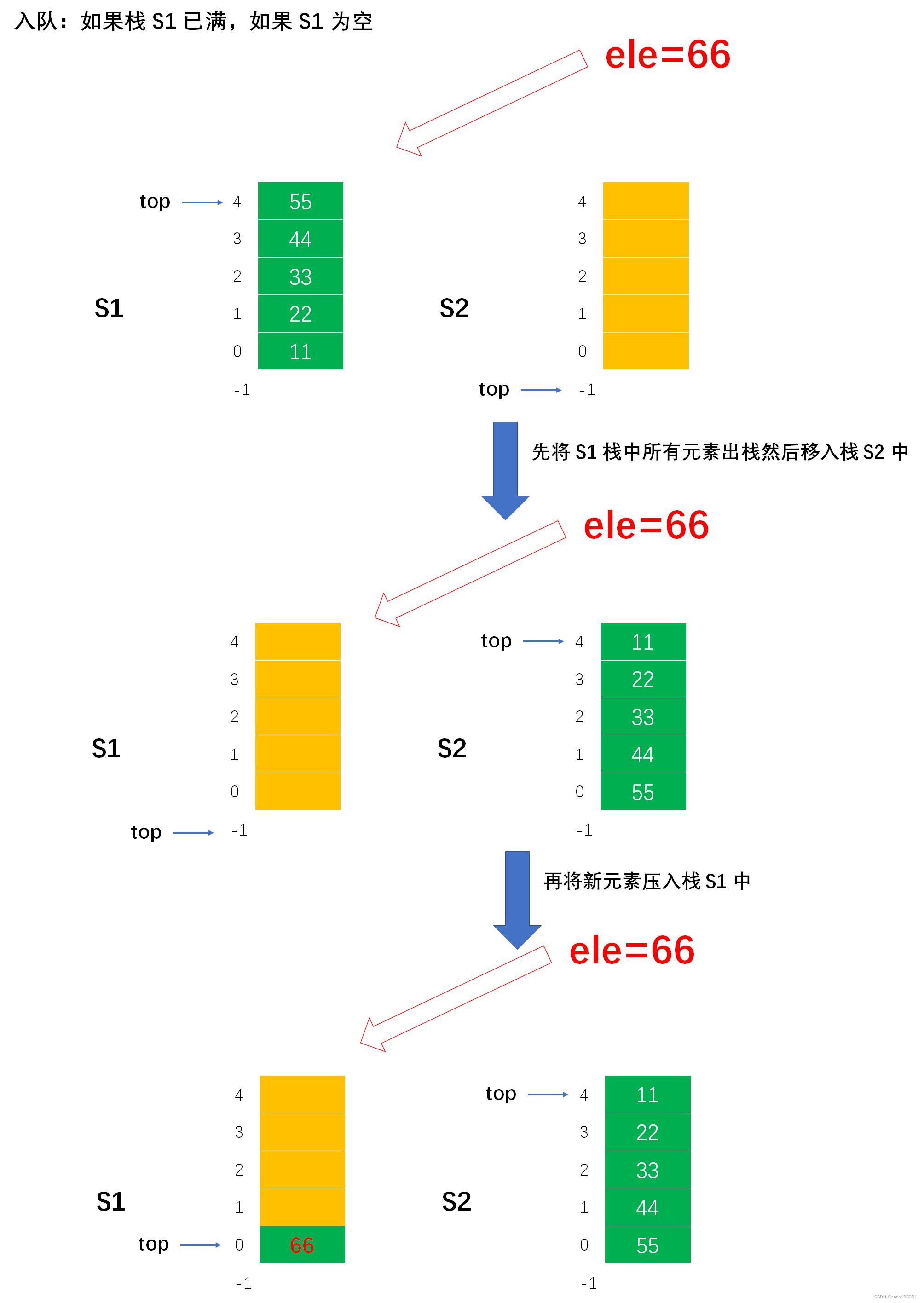
- 出队

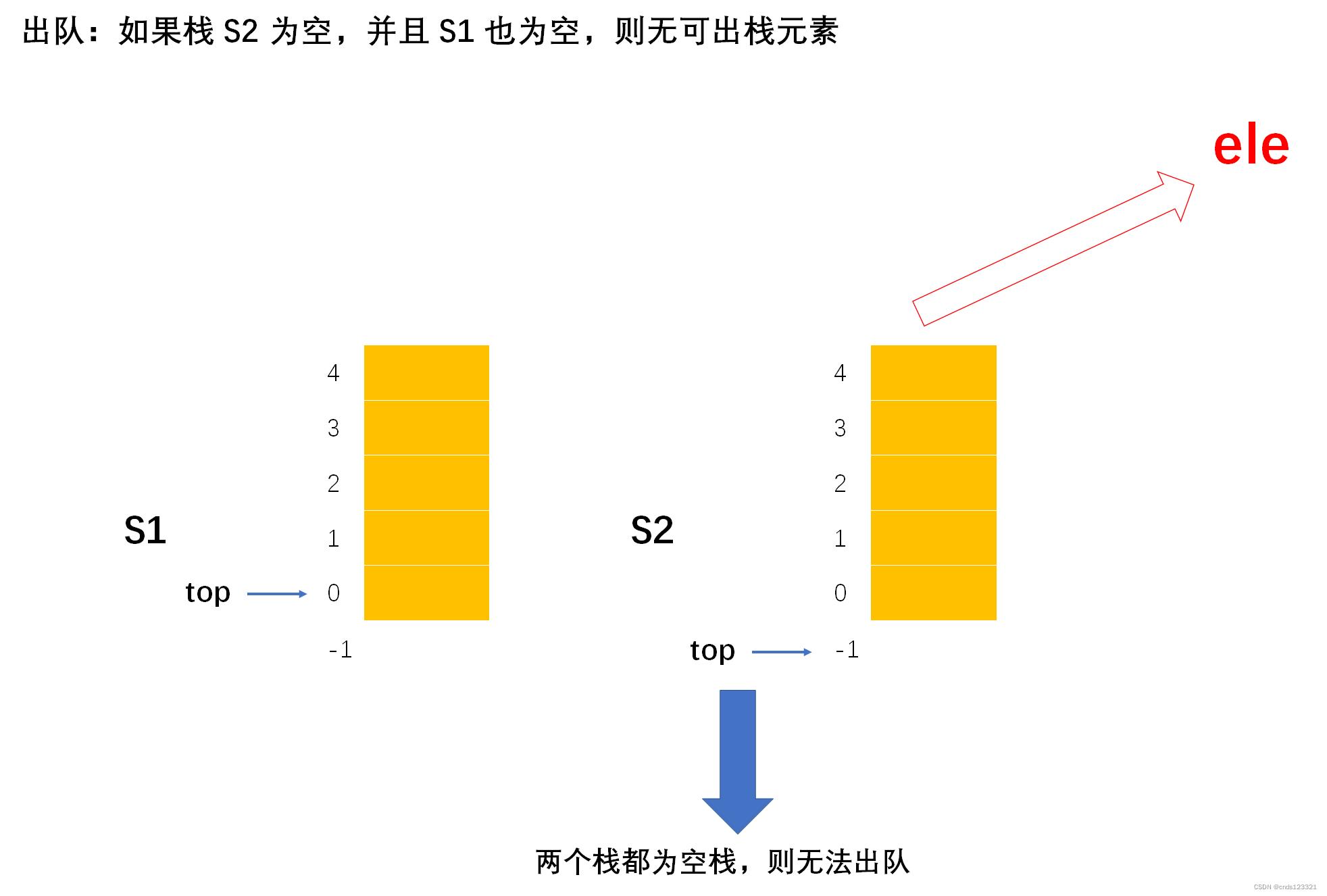

C实现
核心代码:
/**
* 将元素入队
* @param s1 一号栈,存入入队元素
* @param s2 二号栈,存储待出队元素
* @param ele 待入队元素
* @return 如果入队成功则返回 1,否则返回 0 表示入队失败
*/
int enQueue(SeqStack *s1, SeqStack *s2, int ele)
// 1.根据栈 s1 是否满来操作
// 1.1 如果栈 s1 是未满状态,那么可以一直直接将元素压入 s1 中,即使有待出队的元素也是在 s2 中,s1 毫无影响
if (s1->top != MAXSIZE - 1)
push(s1, ele);
// 1.2 如果栈 s1 是已满状态,那说明栈 s1 已经放不下新元素了,那么可以将这些元素全部转移到栈 s2 中,转移之后,栈 s1 又能继续入队新元素了
else
// 1.2.1 在栈 s1 已满的情况下,如果栈 s2 是非空,则不能入栈
// 但是将 s1 中的全部元素转移到 s2 中有一个问题,即要求 s2 是空栈才能转移
// 如果栈 s2 不是空栈,那么就不能将栈 s1 中的元素入栈,因为会影响原栈 s2 中的元素出队,会打乱队列先进先出的特性
if (!isEmpty(*s2))
return 0;
// 1.2.2 如果栈 s2 是空栈,那么就将栈 s1 中所有元素压入栈 s2 中
else
// 1.2.2.1 将 s1 中所有元素压入栈 s2 中
while (!isEmpty(*s1))
// 局部变量,存储从栈 s1 出栈的栈顶元素
int top;
// 将栈 s1 的栈顶元素出栈
pop(s1, &top);
// 将刚才 s1 出出栈的栈顶元素压入栈 s2 中
push(s2, top);
// 1.2.2.2 然后再将新元素压入栈 s1 中
push(s1, ele);
return 1;
/**
* 将元素出队
* @param s1 一号栈,存入入队元素
* @param s2 二号栈,存储待出队元素
* @param ele 用来保存出队的元素
* @return 如果入队成功则返回 1,否则返回 0 表示入队失败
*/
int deQueue(SeqStack *s1, SeqStack *s2, int *ele)
// 局部变量,用来存储栈顶元素
int top;
// 1.根据栈 s2 是否为空来进行操作
// 1.1 如果栈 s2 非空,那么直接将栈 s2 的栈顶元素出栈即可
if (!isEmpty(*s2))
pop(s2, &top);
*ele = top;
// 1.2 如果栈 s2 为空,那么就需要检查下栈 s1 是否有已经入队的元素,如果 s1 中有元素,那么将 s1 中的所有元素压入栈 s2 中,然后将栈 s2 的栈顶元素出栈;如果 s1 中没有元素,则不能出队
else
// 1.2.1 如果栈 s1 也为空,则没有元素可以出队,则返回 0 表示出队失败
if (isEmpty(*s1))
return 0;
// 1.2.2 如果栈 s1 非空,则将 s1 所有元素压入栈 s2 中,然后再将 s2 中的元素进行出栈
else
// 1.2.2.1 将 s1 中的所有元素压入栈 s2 中
while (!isEmpty(*s1))
// 将栈 s1 的栈顶元素出栈
pop(s1, &top);
// 然后将 s1 出栈的栈顶元素压入栈 s2 中
push(s2, top);
// 1.2.2.2 然后将栈 s2 的栈顶元素出栈
pop(s2, &top);// 将栈 s2 的栈顶元素出栈
*ele = top;// 用 ele 保存栈 s2 的出栈元素。其实这两行代码可以写成一步:pop(s2, ele)。
return 1;
/**
* 判断队列是否为空
* @param s1 一号栈,存入入队元素
* @param s2 二号栈,存储待出队元素
* @return 如果队列为空则返回 1,否则返回 0
*/
int isQueueEmpty(SeqStack s1, SeqStack s2)
// 只有栈 s1 和 s2 同时为空,则才表示该队列为空
// 因为栈 s1 是用来存储入队元素的,而栈 s2 用来存储出队元素的,所以只要有一个不为空,那么则表示队列不为空
if (isEmpty(s1) && isEmpty(s2))
return 1;
else
return 0;
完整代码:
#include<stdio.h>
/**
* 顺序栈最大存储的元素个数
*/
#define MAXSIZE 5
/**
* 顺序栈结构体定义
*/
typedef struct
/**
* 数据域,数组,用来存储栈中元素
*/
int data[MAXSIZE];
/**
* 指针域,表示栈顶指针,实际上就是数组下标
*/
int top;
SeqStack;
/**
* 初始化顺序栈,即将栈顶指针指向 -1 表示空栈
* @param stack 顺序栈
*/
void init(SeqStack *stack)
// 设定让栈顶指针指向 -1 表示为栈空
stack->top = -1;
/**
* 判断顺序栈是否为空
* @param stack 顺序栈
* @return 如果顺序栈为空则返回 1,否则返回 0
*/
int isEmpty(SeqStack stack)
// 只需要判断栈顶指针是否等于 -1 即可,如果是空栈则返回 1,不是空栈则返回 0
if (stack.top == -1)
return 1;
else
return 0;
/**
* 将元素入栈
* @param stack 顺序栈
* @param ele 元素值
* @return 如果栈满则返回 0 表示入栈失败;如果插入成功则返回 1
*/
int push(SeqStack *stack, int ele)
// 1.参数校验,如果栈满则不能入栈元素
if (stack->top == MAXSIZE - 1)
// 如果栈满,则返回 0,表示不能入栈
return 0;
// 2.先将栈顶指针加一,指向新空数组位置
stack->top++;
// 3.将新元素值填充到新位置中
stack->data[stack->top] = ele;
return 1;
/**
* 将元素出栈
* @param stack 顺序栈
* @param ele 用来保存出栈的元素
* @return 如果栈空则返回 0 表示出栈失败;否则返回 1 表示出栈成功
*/
int pop(SeqStack *stack, int *ele)
// 1.参数校验,栈空不能出栈
if (stack->top == -1)
// 栈空,没有元素可出栈
return 0;
// 2.用 ele 来保存顺序栈栈顶元素
*ele = stack->data[stack->top];
// 3.然后栈顶指针减一,表示出栈一个元素
stack->top--;
return 1;
/**
* 将元素入队
* @param s1 一号栈,存入入队元素
* @param s2 二号栈,存储待出队元素
* @param ele 待入队元素
* @return 如果入队成功则返回 1,否则返回 0 表示入队失败
*/
int enQueue(SeqStack *s1, SeqStack *s2, int ele)
// 1.根据栈 s1 是否满来操作
// 1.1 如果栈 s1 是未满状态,那么可以一直直接将元素压入 s1 中,即使有待出队的元素也是在 s2 中,s1 毫无影响
if (s1->top != MAXSIZE - 1)
push(s1, ele);
// 1.2 如果栈 s1 是已满状态,那说明栈 s1 已经放不下新元素了,那么可以将这些元素全部转移到栈 s2 中,转移之后,栈 s1 又能继续入队新元素了
else
// 1.2.1 在栈 s1 已满的情况下,如果栈 s2 是非空,则不能入栈
// 但是将 s1 中的全部元素转移到 s2 中有一个问题,即要求 s2 是空栈才能转移
// 如果栈 s2 不是空栈,那么就不能将栈 s1 中的元素入栈,因为会影响原栈 s2 中的元素出队,会打乱队列先进先出的特性
if (!isEmpty(*s2))
return 0;
// 1.2.2 如果栈 s2 是空栈,那么就将栈 s1 中所有元素压入栈 s2 中
else
// 1.2.2.1 将 s1 中所有元素压入栈 s2 中
while (!isEmpty(*s1))
// 局部变量,存储从栈 s1 出栈的栈顶元素
int top;
// 将栈 s1 的栈顶元素出栈
pop(s1, &top);
// 将刚才 s1 出出栈的栈顶元素压入栈 s2 中
push(s2, top);
// 1.2.2.2 然后再将新元素压入栈 s1 中
push(s1, ele);
return 1;
/**
* 将元素出队
* @param s1 一号栈,存入入队元素
* @param s2 二号栈,存储待出队元素
* @param ele 用来保存出队的元素
* @return 如果入队成功则返回 1,否则返回 0 表示入队失败
*/
int deQueue(SeqStack *s1, SeqStack *s2, int *ele)
// 局部变量,用来存储栈顶元素
int top;
// 1.根据栈 s2 是否为空来进行操作
// 1.1 如果栈 s2 非空,那么直接将栈 s2 的栈顶元素出栈即可
if (!isEmpty(*s2))
pop(s2, &top);
*ele = top;
// 1.2 如果栈 s2 为空,那么就需要检查下栈 s1 是否有已经入队的元素,如果 s1 中有元素,那么将 s1 中的所有元素压入栈 s2 中,然后将栈 s2 的栈顶元素出栈;如果 s1 中没有元素,则不能出队
else
// 1.2.1 如果栈 s1 也为空,则没有元素可以出队,则返回 0 表示出队失败
if (isEmpty(*s1))
return 0;
// 1.2.2 如果栈 s1 非空,则将 s1 所有元素压入栈 s2 中,然后再将 s2 中的元素进行出栈
else
// 1.2.2.1 将 s1 中的所有元素压入栈 s2 中
while (!isEmpty(*s1))
// 将栈 s1 的栈顶元素出栈
pop(s1, &top);
// 然后将 s1 出栈的栈顶元素压入栈 s2 中
push(s2, top);
// 1.2.2.2 然后将栈 s2 的栈顶元素出栈
pop(s2, &top);// 将栈 s2 的栈顶元素出栈
*ele = top;// 用 ele 保存栈 s2 的出栈元素。其实这两行代码可以写成一步:pop(s2, ele)。
return 1;
/**
* 判断队列是否为空
* @param s1 一号栈,存入入队元素
* @param s2 二号栈,存储待出队元素
* @return 如果队列为空则返回 1,否则返回 0
*/
int isQueueEmpty(SeqStack s1, SeqStack s2)
// 只有栈 s1 和 s2 同时为空,则才表示该队列为空
// 因为栈 s1 是用来存储入队元素的,而栈 s2 用来存储出队元素的,所以只要有一个不为空,那么则表示队列不为空
if (isEmpty(s1) && isEmpty(s2))
return 1;
else
return 0;
int main()
// 声明两个顺序栈并初始化
SeqStack s1;
init(&s1);
SeqStack s2;
init(&s2);
// 是否队空
printf("\\n是否队空:\\n");
int empty;
empty = isQueueEmpty(s1, s2);
printf("%d\\n", empty);
// 将元素入队
enQueue(&s1, &s2, 11);
enQueue(&s1, &s2, 22);
enQueue(&s1, &s2, 33);
enQueue(&s1, &s2, 44);
enQueue(&s1, &s2, 55);
enQueue(&s1, &s2, 66);
enQueue(&s1, &s2, 77);
// 将元素出队
printf("\\n将元素出队:\\n");
int ele;
deQueue(&s1, &s2, &ele);
printf("出队元素:%d\\n", ele);
deQueue(&s1, &s2, &ele);
printf("出队元素:%d\\n", ele);
deQueue(&s1, &s2, &ele);
printf("出队元素:%d\\n", ele);
deQueue(&s1, &s2, &ele);
printf("出队元素:%d\\n", ele);
执行结果:
是否队空:
1
将元素出队:
出队元素:11
出队元素:22
出队元素:33
出队元素:44
Java实现
核心代码:
/**
* 将元素入队
*
* @param s1 一号栈,存入入队元素
* @param s2 二号栈,存储待出队元素
* @param ele 待入队元素
* @throws Exception s1 已满,s2 非空不能入队则抛出该异常
*/
public static void enQueue(SeqStack s1, SeqStack s2, int ele) throws Exception
// 1.根据栈 s1 是否满来操作
// 1.1 如果栈 s1 是未满状态,那么可以一直直接将元素压入 s1 中,即使有待出队的元素也是在 s2 中,s1 毫无影响
if (!s1.isFull())
s1.push(ele);
// 1.2 如果栈 s1 是已满状态,那说明栈 s1 已经放不下新元素了,那么可以将这些元素全部转移到栈 s2 中,转移之后,栈 s1 又能继续入队新元素了
else
// 1.2.1 在栈 s1 已满的情况下,如果栈 s2 是非空,则不能入栈
// 但是将 s1 中的全部元素转移到 s2 中有一个问题,即要求 s2 是空栈才能转移
// 如果栈 s2 不是空栈,那么就不能将栈 s1 中的元素入栈,因为会影响原栈 s2 中的元素出队,会打乱队列先进先出的特性
if (!s2.isEmpty())
throw new Exception("s1 已满,s2 非空因此不能入队!");
// 1.2.2 如果栈 s2 是空栈,那么就将栈 s1 中所有元素压入栈 s2 中
else
// 1.2.2.1 将 s1 中所有元素压入栈 s2 中
while (!s1.isEmpty())
// 将栈 s1 的栈顶元素出栈
int top = s1.pop();
// 将刚才 s1 出出栈的栈顶元素压入栈 s2 中
s2.push(top);
// 1.2.2.2 然后再将新元素压入栈 s1 中
s1.push(ele);
/**
* 将元素出队
*
* @param s1 一号栈,存入入队元素
* @param s2 二号栈,存储待出队元素
* @return 用来保存出队的元素
* @throws Exception 如果栈 s1 和 s2 均为空则抛出此异常
*/
public static int deQueue(SeqStack s1, SeqStack s2) throws Exception
// 局部变量,用来存储栈顶元素,即出队元素
int ele = 0;
// 1.根据栈 s2 是否为空来进行操作
// 1.1 如果栈 s2 非空,那么直接将栈 s2 的栈顶元素出栈即可
if (!s2.isEmpty())
ele = s2.pop();
// 1.2 如果栈 s2 为空,那么就需要检查下栈 s1 是否有已经入队的元素,如果 s1 中有元素,那么将 s1 中的所有元素压入栈 s2 中,然后将栈 s2 的栈顶元素出栈;如果 s1 中没有元素,则不能出队
else
// 1.2.1 如果栈 s1 也为空,则没有元素可以出队,则抛出异常表示出队失败
if (s1.isEmpty())
throw new Exception("s1 和 s2 均为空无可出队元素!");
// 1.2.2 如果栈 s1 非空,则将 s1 所有元素压入栈 s2 中,然后再将 s2 中的元素进行出栈
else
// 1.2.2.1 将 s1 中的所有元素压入栈 s2 中
while (!s1.isEmpty())
// 将栈 s1 的栈顶元素出栈
ele = s1.pop();
// 然后将 s1 出栈的栈顶元素压入栈 s2 中
s2.push(ele);
// 1.2.2.2 然后将栈 s2 的栈顶元素出栈,即出队元素
ele = s2.pop();
// 最后返回出队元素
return ele;
/**
* 判断队列是否为空
*
* @param s1 一号栈,存入入队元素
* @param s2 二号栈,存储待出队元素
* @return 如果队列为空则返回 1,否则返回 0
*/
public static boolean isQueueEmpty(SeqStack s1, SeqStack s2)
return s1.isEmpty() && s2.isEmpty();
完整代码:
public class Test
public static void main(String[] args) throws Exception
// 声明两个顺序栈并初始化
SeqStack s1 = new SeqStack();
s1.init();
SeqStack s2 = new SeqStack();
s2.init();
// 是否队空
System.out.println("\\n是否队空:");
boolean empty;
empty = isQueueEmpty(s1, s2);
System.out.println(empty);
// 将元素入队
enQueue(s1, s2, 11);
enQueue(s1, s2, 22);
enQueue(s1, s2, 33);
enQueue(s1, s2, 44);
enQueue(s1, s2, 55);
enQueue(s1, s2, 66);
enQueue(s1, s2, 77);
// 将元素出队
System.out.println("\\n将元素出队:");
int ele;
ele = deQueue(s1, s2);
System.out.println("出队元素:" + ele);
ele = deQueue(s1, s2);
System.out.println("出队元素:" + ele);
ele = deQueue(s1, s2);
System.out.println("出队元素:" + ele);
ele = deQueue(s1, s2);
System.out.println("出队元素:" + ele);
/**
* 将元素入队
*
* @param s1 一号栈,存入入队元素
* @param s2 二号栈,存储待出队元素
* @param ele 待入队元素
* @throws Exception s1 已满,s2 非空不能入队则抛出该异常
*/
public static void enQueue(SeqStack s1, SeqStack s2, int ele) throws Exception
// 1.根据栈 s1 是否满来操作
// 1.1 如果栈 s1 是未满状态,那么可以一直直接将元素压入 s1 中,即使有待出队的元素也是在 s2 中,s1 毫无影响
if (!s1.以上是关于队列练习之Example001-用两个栈 s1 和 s2 来模拟一个队列,实现队列的出队入队队是否为空的运算的主要内容,如果未能解决你的问题,请参考以下文章
线性表练习之Example001-创建不重复字母字符的单链表
线性表练习之Example029-求两个等长升序序列 A 和 B 的中位数
队列练习之Example005-Q 是一个队列,S 是一个空栈,实现将队列中的元素逆置的算法
队列练习之Example004-设计一个循环队列,用 front 和 rear 分别作为队头和队尾指针,另外用一个标志 tag 表示队列是空还是不空