机器学习（20）——循环神经网络

Posted 2022-05-11 进击的南方仔

文章目录

• 1 RNN 的缺点
• 2 LSTM
• • 2.1 遗忘门
  • 2.2 输入门
  • 2.3 输出门
  • 3.4 小结
• 3 GRU
• • 3.1 复位门
  • 3.2 更新门
  • 3.3 小结

1 RNN 的缺点

  我在上一篇博客中跟大家一步一步探索了 RNN 模型的网络结构，最后面也介绍了 RNN 的应用场景。但在实际应用中，标准 RNN 训练的优化算法面临一个很大的难题，就是长期依赖问题——由于网络结构的变深使得模型丧失了学习到先前信息的能力，通俗的说，标准的 RNN 虽然有了记忆，但很健忘，也即标准 RNN 只有短时记忆。循环神经网络在处理较长的句子时，往往只能够理解有限长度内的信 息，而对于位于较长范围类的有用信息往往不能够很好的利用起来。我们把这种现象叫做短时记忆。
  针对标准 RNN 短时记忆的问题，最直接的想法就是延长这种短时记忆，使得 RNN 可以有效利用较大范围内的训练数据，从而提升性能。这时，一种基于 RNN 改进的新型网络模型——LSTM 该登场了。同时在上篇博客的最后面谈到了 RNN 的梯度消失问题，LSTM 模型可以有效地解决这个问题。

2 LSTM

  1997 年，瑞士人工智能科学家 Jürgen Schmidhuber 提出了 长短时记忆网络(Long Short-Term Memory，简称 LSTM)。LSTM 相对于基础的 RNN 网络来说，记忆能力更强，更擅长处理较长的序列信号数据，LSTM 提出后，被广泛应用在序列预测、自然语言处理等任务中，几乎取代了基础的 RNN 模型。
  首先回顾一下基础的 RNN 网络结构：

上一个时间戳的状态向量 ${\mathbf{h}}_{\mathbf{t}-1}$ 与当前时间戳的输入 ${\mathbf{x}}_{\mathbf{t}}$ 经过线性变换后，通过激活函数 $\mathbf{t}\mathbf{a}\mathbf{n}\mathbf{h}$ 后得到新的状态向量 ${\mathbf{h}}_{\mathbf{t}}$。相对于基础的 RNN，网络只有一个状态向量 ${\mathbf{h}}_{\mathbf{t}}$，LSTM 新增了一个状态向量 ${\mathbf{C}}_{\mathbf{t}}$，同时引入了 门控(Gate)机制，通过门控单元来控制信息的遗忘和刷新：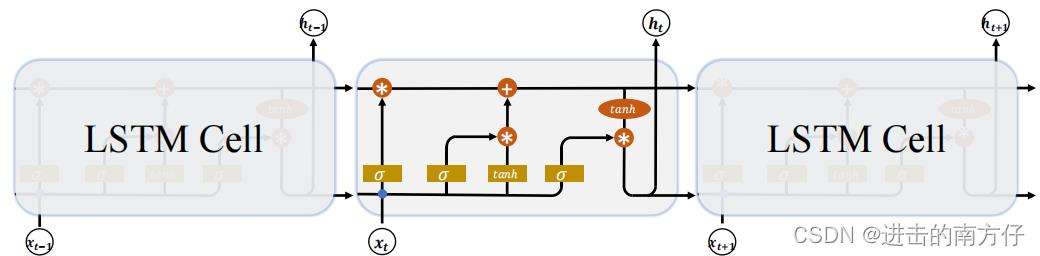
  在 LSTM Cell 中，有两个状态向量 $\mathbf{c}$ 和 $\mathbf{h}$，其中 $\mathbf{c}$ 作为 LSTM 的内部状态向量，可以理解为 LSTM 的 内存状态向量 Memory，而 $\mathbf{h}$ 表示 LSTM 的输出向量。相对于基础的 RNN 来说，LSTM 把内部 Memory 和输出分开为两个变量，同时利用三个门控：输入门(Input Gate)、遗忘门(Forget Gate)和输出门(Output Gate)来控制内部信息的流动。
  门控机制可以理解为控制数据流通量的一种手段，类比于水阀门：当水阀门全部打开时，水流畅通无阻地通过；当水阀门全部关闭时，水流完全被隔断。在 LSTM 中，阀门开和程度利用门控值向量 $\mathbf{g}$ 表示：

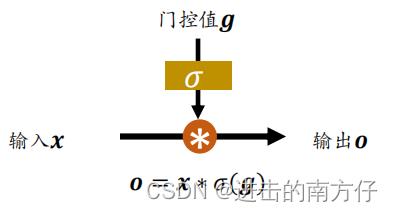
上图中通过 $\mathbf{\sigma }(\mathbf{g})$ 激活函数将门控值压缩到 $[0,1]$ 之间，当 $\mathbf{\sigma }(\mathbf{g})=0$ 时，门控全部关闭，输出 $\mathbf{o}=0$；当 $\mathbf{\sigma }(\mathbf{g})=1$ 时，门控全部打开，输出 $\mathbf{o}=\mathbf{x}$。通过门控机制可以较好地控制数据的流量程度。

---

注：到此您可以跳转至 3 GUR 阅读完 GUR 的原理之后再回来阅读 LSTM，因 GUR 结构较为简单。

---

2.1 遗忘门

  遗忘门作用于 LSTM 状态向量 $\mathbf{c}$，用于控制上一个时间戳的记忆 ${\mathbf{c}}_{\mathbf{t}-1}$ 对当前时间戳的影响。

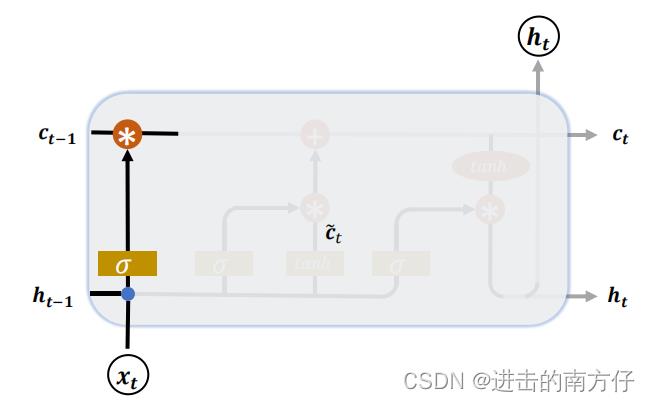
遗忘门的控制变量 ${\mathbf{g}}_{\mathbf{f}}$ 计算过程如下：
$${\mathbf{g}}_{\mathbf{f}}=\mathbf{\sigma }({\mathbf{W}}_{\mathbf{f}}[{\mathbf{h}}_{\mathbf{t}-1};{\mathbf{x}}_{\mathbf{t}}]+{\mathbf{b}}_{\mathbf{f}})$$
其中 ${\mathbf{W}}_{\mathbf{f}}$ 和 ${\mathbf{b}}_{\mathbf{f}}$ 为遗忘门的参数张量，可由反向传播算法自动优化，$\mathbf{\sigma }$ 为激活函数，一般使用 Sigmoid 函数。当 ${\mathbf{g}}_{\mathbf{f}}=1$ 时，遗忘门全部打开，LSTM 接受上一个状态 ${\mathbf{c}}_{\mathbf{t}-1}$ 的所有信息 ；当 ${\mathbf{g}}_{\mathbf{f}}=0$ 时，遗忘门关闭，LSTM 直接忽略 ${\mathbf{c}}_{\mathbf{t}-1}$ 的所有信息输出为 0 的向量。这也是遗忘门的名字由来。经过遗忘门后，LSTM 的状态向量 ${\mathbf{c}}_{\mathbf{t}}$ 变为 ${\mathbf{g}}_{\mathbf{f}}{\mathbf{c}}_{\mathbf{t}-1}$。

2.2 输入门

  输入门用于控制 LSTM 对输入的接收程度。

首先通过对当前时间戳的输入 ${\mathbf{x}}_{\mathbf{t}}$ 和上一个时间戳的输出 ${\mathbf{h}}_{\mathbf{t}-1}$ 做非线性变换得到新的输入向量 $\widetilde{{\mathbf{c}}_{\mathbf{t}}}$：
$$\widetilde{{\mathbf{c}}_{\mathbf{t}}}=\mathbf{t}\mathbf{a}\mathbf{n}\mathbf{h}({\mathbf{W}}_{\mathbf{c}}[{\mathbf{h}}_{\mathbf{t}-1};{\mathbf{x}}_{\mathbf{t}}]+{\mathbf{b}}_{\mathbf{c}})$$
其中 ${\mathbf{W}}_{\mathbf{c}}$ 和 ${\mathbf{b}}_{\mathbf{c}}$ 为输入门的参数，需要通过反向传播算法自动优化，$\mathbf{t}\mathbf{a}\mathbf{n}\mathbf{h}$ 为激活函数，用于将输入标准化到 $[-1,1]$ 区间。$\widetilde{{\mathbf{c}}_{\mathbf{t}}}$ 并不会全部刷新进入 LSTM 的 Memory，而是通过输入门控制接受输入的量。输入门的控制变量同样来自于输入 ${\mathbf{x}}_{\mathbf{t}}$ 和输出 ${\mathbf{h}}_{\mathbf{t}-1}$：
$${\mathbf{g}}_{\mathbf{i}}=\mathbf{\sigma }({\mathbf{W}}_{\mathbf{i}}[{\mathbf{h}}_{\mathbf{t}-1};{\mathbf{x}}_{\mathbf{t}}]+{\mathbf{b}}_{\mathbf{i}})$$
其中 ${\mathbf{W}}_{\mathbf{i}}$ 和 ${\mathbf{b}}_{\mathbf{i}}$ 为输入门的参数，可由反向传播算法自动优化，$\mathbf{\sigma }$ 为激活函数，一般使用 Sigmoid 函数。输入门控制变量 ${\mathbf{g}}_{\mathbf{i}}$ 决定了 LSTM 对当前时间戳的新输入 $\widetilde{{\mathbf{c}}_{\mathbf{t}}}$ 的接受程度：当 g i