Neural Factorization Machines（NFM）

Posted 2022-05-07 zhiyong_will

1. 概述

Neural Factorization Machines（NFM）[1]是在2017年提出的用于求解CTR问题的算法模型，在Wide & Deep模型被提出后，相继出现了一些改进的算法模型，如DeepFM和DCN可以看成是对于Wide & Deep模型中Wide部分的改进，而此处的NFM模型则是可以看作是对Deep部分的改进。从模型的名字来看，NFM包含了两个部分，第一为Neural，这部分与神经网络相关，第二为Factorization Machines，这部分与FM相关。对于FM模型，文章中提到了可以从深度学习网络结构的角度来看待，此时FM就可以看作是由单层LR和二阶特征交叉组成的Wide & Deep模型，与Google提出的Wide & Deep模型的不同之处就是Deep部分是二阶隐向量相乘。从这个角度上来看，NFM是在FM的基础上利用NN模型代替FM中的Deep部分，而这个NN与Wide & Deep中的Deep的不同是NFM中的Deep中包含了Bi-Interaction的层，用于对特征做二阶交叉运算。综上，NFM的优化点主要为：

1. 在深度网络中引入Bi-Interaction做进一步的特征交叉。
2. 对比FM，深度网络能够学习更高阶的非线形的特征交叉。

2. 算法原理

2.1. NFM模型的网络结构

完整的NFM的网络结构如下图所示：

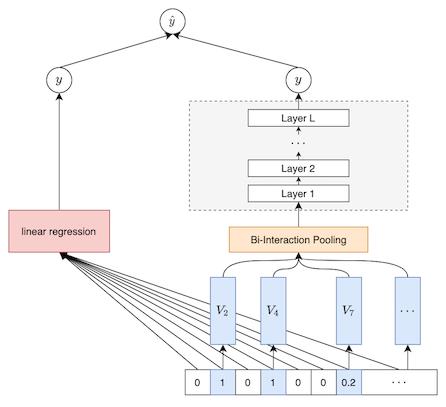
对于NFM模型，假设输入的稀疏经one-hot编码后的向量为$\mathbf{x}\in {\mathbb{R}}^n$，NFM模型的输出为：

$${\hat{y}}_{NFM}\left(\mathbf{x}\right)=w_0+\sum _{i=1}^n{w}_i{x}_i+f\left(\mathbf{x}\right)$$

其中，$w_0+{\sum }_{i=1}^n{w}_i{x}_i$如上图中的linear regression，$f\left(\mathbf{x}\right)$为上图中的右半部分。对于FM算法，其表达式为：

$${\hat{y}}_{FM}\left(\mathbf{x}\right)=w_0+\sum _{i=1}^n{w}_i{x}_i+\sum _{i=1}^{n-1}\sum _{j=i+1}^n⟨v_i,v_j⟩x_i{x}_j$$

从两者的数学表达式可以看出，FM模型是NFM的特殊形式，即满足：$f\left(\mathbf{x}\right)={\sum }_{i=1}^{n-1}{\sum }_{j=i+1}^n⟨v_i,v_j⟩x_i{x}_j$。我们发现如何构造$f\left(\mathbf{x}\right)$式NFM模型中的关键部分。

2.2. NFM模型中的特征交叉

NFM模型中的特征交叉$f\left(\mathbf{x}\right)$的结构如下图所示：

如上图，NFM中特征交叉部分$f\left(\mathbf{x}\right)$是一个深度神经网络模型，在特征交叉部分$f\left(\mathbf{x}\right)$的网络中，主要包括Embedding层，Bi-Interaction层，隐含层以及预测层。

2.2.1. Embedding层

Embedding层的作用是将稀疏的one-hot特征转换成稠密的向量表示，这个操作是深度神经网络的必备操作方法。假设转换后的embeding向量为：

$${\mathbf{V}}_x=x_1{\mathbf{v}}_1,\cdots ,x_n{\mathbf{v}}_n$$

2.2.2. Bi-Interaction层

对稀疏特征处理后就可以进入到深度学习模型的计算中，在NFM中，首先进入到Bi-Interaction层中，Bi-Interaction Pooling的主要作用是对Embedding后的特征学习特征交叉，其具体格式为：

$$f_{BI}\left({\mathbf{V}}_x\right)=\sum _{i=1}^{n-1}\sum _{j=i+1}^n{x}_i{\mathbf{v}}_i\odot x_j{\mathbf{v}}_j$$

其中，$\odot$表示的是两个向量的元素乘积，即${\left({\mathbf{v}}_i\odot {\mathbf{v}}_j\right)}_k=v_{ik}{v}_{jk}$。可以看到Bi-Interaction的输出为两个向量的交叉。

2.2.3. Hidden层

在Bi-Interaction层之上是堆叠了一系列的隐含层，主要的目的是学习更高阶的特征交叉，用数学的表述为：

$$\begin{array}{c}{\mathbf{z}}_1={\sigma }_1({\mathbf{W}}_1{f}_{以上是关于Neural\; Factorization\; Machines（NFM）的主要内容，如果未能解决你的问题，请参考以下文章}\end{array}$$

Neural Factorization Machines（NFM）

推荐系统DeepFM模型（A Factorization-Machine based Neural Network）

推荐系统DeepFM模型（A Factorization-Machine based Neural Network）

DeepFM: A Factorization-Machine based Neural Network for CTR Prediction 阅读笔记

推荐系统论文精读系列(十四)--Information Fusion-Based Deep Neural Attentive Matrix Factorization Recommendation

LeetCode Minimum Factorization