ACM入门之连通性
Posted 辉小歌
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了ACM入门之连通性相关的知识,希望对你有一定的参考价值。
目录
有向图的强连通分量
对于一个有向图,连通分量: 对于分量中任意两点u,v,必然可以从u走到v,且从v走到u。
强连通分量:极大连通分量。也就是说再大点图就不连通了。
常用的求有向图的强连通分量的做法是Tarjan算法求强连通分量(SCC) 时间复杂度O(n+m)
Tarjan算法求强连通分量的思路是:对于每一个点定义两个时间戳。
dfn[u]表示遍历到u的时间戳。low[u]从u开始走,所能遍历到的最小时间戳是什么。
u是其所在的强联通分量的最高点,等价于dfn[u]==low[u]
应用:
我们可以将一张图的每个强连通分量都缩成一个点(简称缩点)。
然后这张图会变成一个 DAG(有向无环图),可以进行拓扑排序以及更多其他操作。
举个简单的例子,求一条路径,可以经过重复结点,要求经过的不同结点数量最多。
例题一:

#include<bits/stdc++.h>
using namespace std;
const int N=1e4*5+10;
int h[N],e[N],ne[N],idx;
int dfn[N],low[N],timestep,scc_cnt;
int in_st[N],id[N],Size[N];
int dout[N];
stack<int>st;
int n,m;
void add(int a,int b)
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
void tarjan(int u)
dfn[u]=low[u]=++timestep;
st.push(u),in_st[u]=1;
for(int i=h[u];i!=-1;i=ne[i])
int j=e[i];
if(!dfn[j])
tarjan(j);
low[u]=min(low[u],low[j]);
else if(in_st[j])low[u]=min(low[u],dfn[j]);
if(dfn[u]==low[u])
++scc_cnt;
int y;
do
y=st.top(); st.pop();
in_st[y]=0;
id[y]=scc_cnt;
Size[scc_cnt]++;
while(y!=u);
int main(void)
cin>>n>>m;
memset(h,-1,sizeof h);
while(m--)
int a,b; cin>>a>>b;
add(a,b);
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i);
for(int i=1;i<=n;i++)//缩点
for(int j=h[i];j!=-1;j=ne[j])
int k=e[j];
int a=id[i],b=id[k];
if(a!=b) dout[a]++;
int zeros=0,sum=0;
for(int i=1;i<=scc_cnt;i++)
if(!dout[i])
zeros++;
sum+=Size[i];
if(zeros>1)
sum=0;
break;
cout<<sum<<endl;
return 0;
例题二:
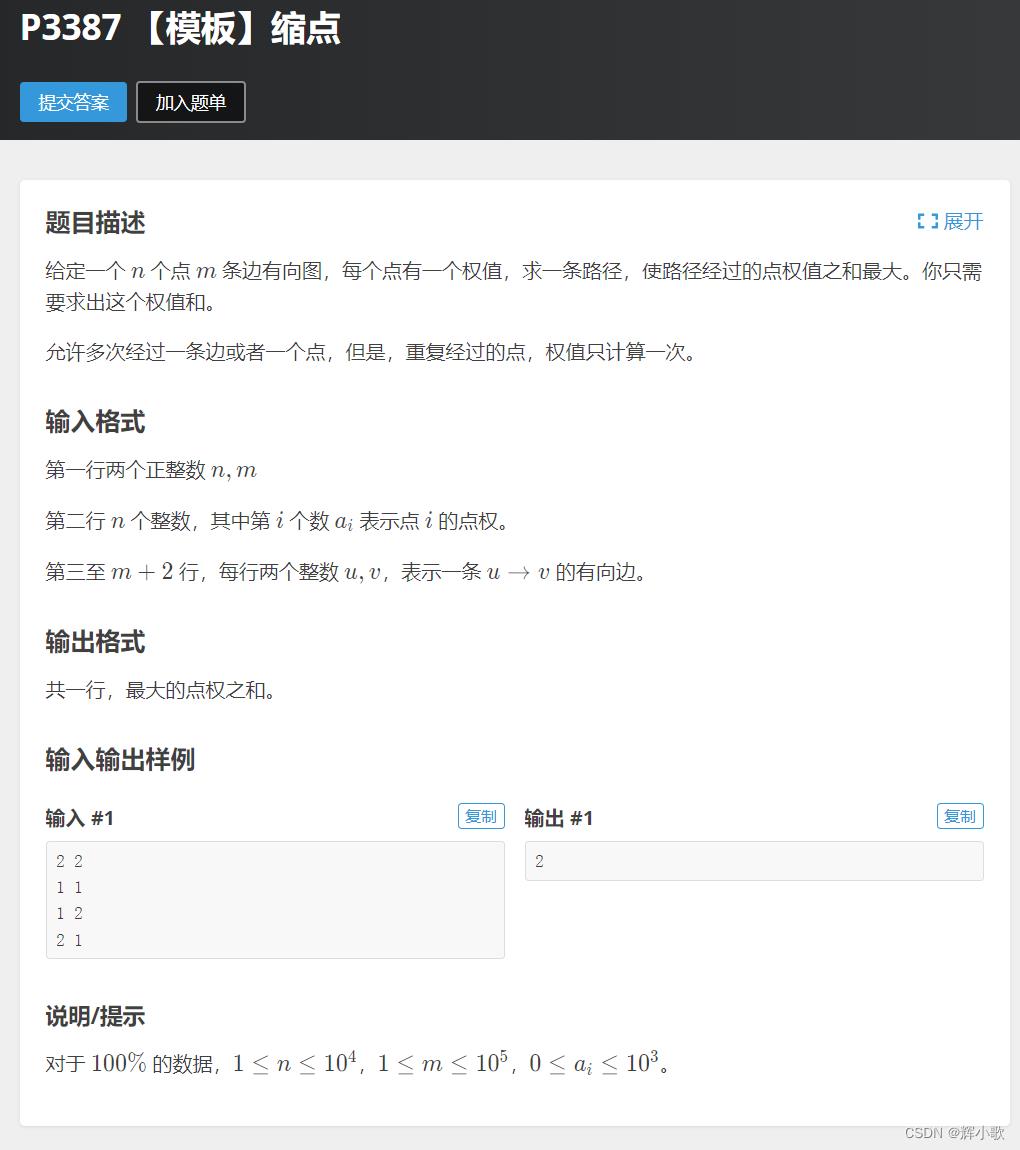
模板题,就是先tarjan一下,然后缩点。根据缩点后的东西建一个新的图,此时是一个有向无环图。
然后拓扑跑一下,推一下即可。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5*2+10;
int h[N],e[N],ne[N],w[N],idx;
int dfn[N],low[N],scc_cnt,timestep;
int id[N],in_st[N],Size[N];
int din[N];
stack<int>st;
int n,m;
void add(int a,int b)
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
void tarjan(int u)
dfn[u]=low[u]=++timestep;
st.push(u),in_st[u]=1;
for(int i=h[u];i!=-1;i=ne[i])
int j=e[i];
if(!dfn[j])
tarjan(j);
low[u]=min(low[u],low[j]);
else if(in_st[j])low[u]=min(low[u],dfn[j]);
if(dfn[u]==low[u])
int y;
++scc_cnt;
do
y=st.top(); st.pop();
id[y]=scc_cnt;
in_st[y]=0;
Size[scc_cnt]+=w[y];
while(y!=u);
void init()
memset(h,-1,sizeof h);
idx=0;
void topsort()//拓扑 递推
queue<int>q;
int dist[N]=0,ans=0;
for(int i=1;i<=scc_cnt;i++)
if(din[i]==0) q.push(i);
dist[i]=w[i];
while(q.size())
int u=q.front(); q.pop();
for(int i=h[u];i!=-1;i=ne[i])
int j=e[i];
if(--din[j]==0) q.push(j);
dist[j]=max(dist[j],dist[u]+w[j]);
for(int i=1;i<=scc_cnt;i++) ans=max(ans,dist[i]);
cout<<ans<<endl;
int main(void)
memset(h,-1,sizeof h);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>w[i];
while(m--)
int a,b; cin>>a>>b;
add(a,b);
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i);
vector< pair<int,int> >edge;
for(int i=1;i<=n;i++)
for(int j=h[i];j!=-1;j=ne[j])
int k=e[j];
int a=id[i],b=id[k];
if(a!=b)
edge.push_back(a,b);
din[b]++;
for(int i=1;i<=scc_cnt;i++) w[i]=Size[i];
init();
for(int i=0;i<edge.size();i++)//重新建图
int a=edge[i].first,b=edge[i].second;
add(a,b);
topsort();
return 0;
无向图的双连通分量
- 在一张连通的无向图中,对于两个点u和v,如果无论删去哪条边(只能删去一条)都不能使它们不连通,
我们就说u和v边双连通。 - 在一张连通的无向图中,对于两个点u和v,如果无论删去哪个点(只能删去一个,且不能删 u和v自己)都不能使它们不连通,
我们就说u和v点双连通。
割点: 删除该点后图不连通。那么这个点就是这个图的割点(又称割顶)。
割边: 删除该边后图不连通。 那么这个边就是这个图的割边(又称桥)。
例题一:
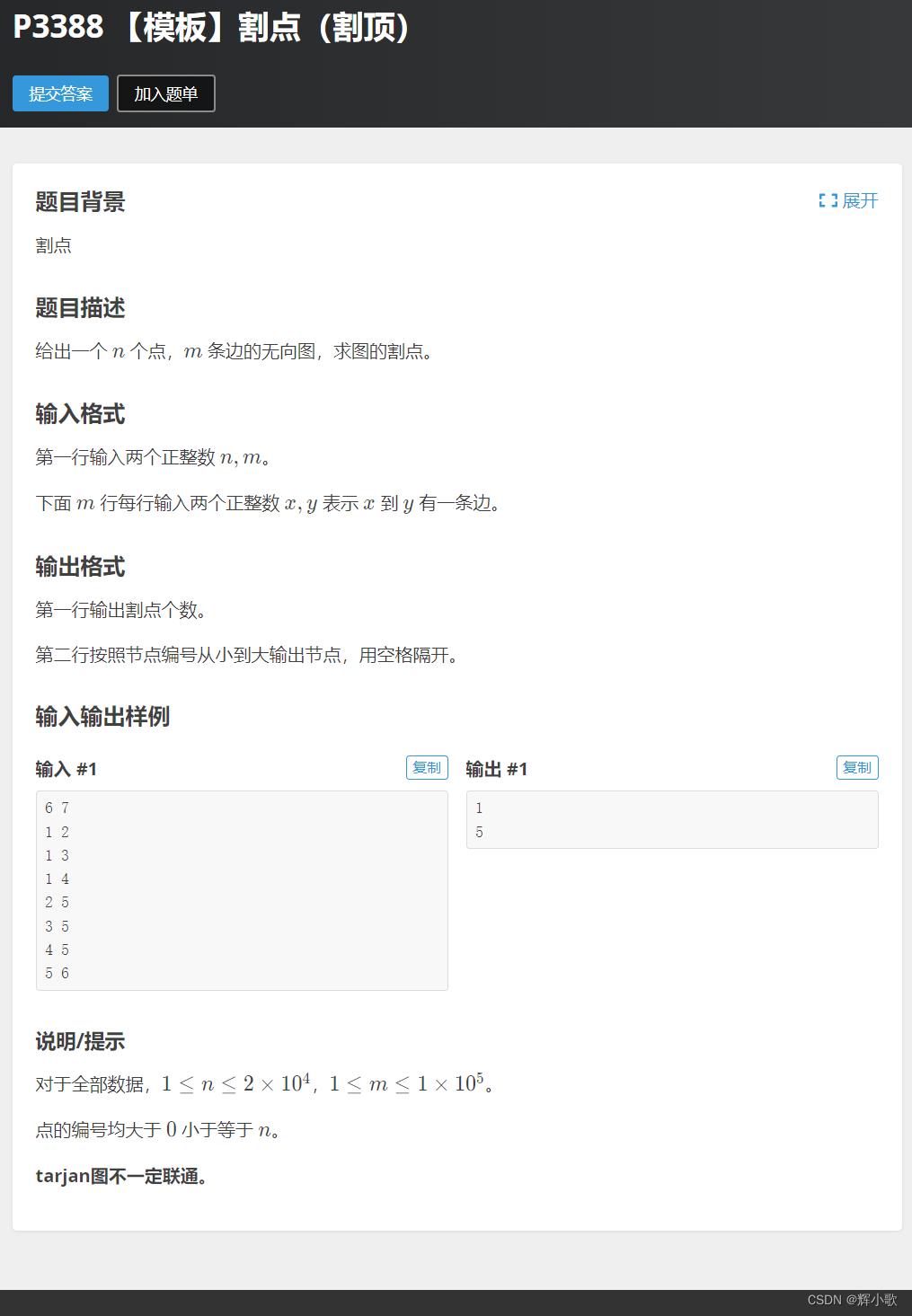
#include<bits/stdc++.h>
using namespace std;
const int N=1e5*6+10;
const int M=1e5*6+10;
int h[N],e[M],ne[M],idx;
int dfn[N],low[N],timestep;
int st[N];
int n,m;
void add(int a,int b)
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
void tarjan(int u,int fa)
dfn[u]=low[u]=++timestep;
int cnt=0;
for(int i=h[u];i!=-1;i=ne[i])
int j=e[i];
if(!dfn[j])
tarjan(j,fa);
low[u]=min(low[u],low[j]);
if(low[j]>=dfn[u]&&u!=fa) st[u]=1;
if(u==fa) cnt++;
else low[u]=min(low[u],dfn[j]);
if(cnt>=2&&u==fa) st[u]=1;
int main(void)
memset(h,-1,sizeof h);
cin>>n>>m;
while(m--)
int a,b;cin>>a>>b;
add(a,b),add(b,a);
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i,i);
int cnt=0;
for(int i=1;i<=n;i++) if(st[i]) cnt++;
cout<<cnt<<endl;
for(int i=1;i<=n;i++) if(st[i]) cout<<i<<" ";
return 0;
例题二:
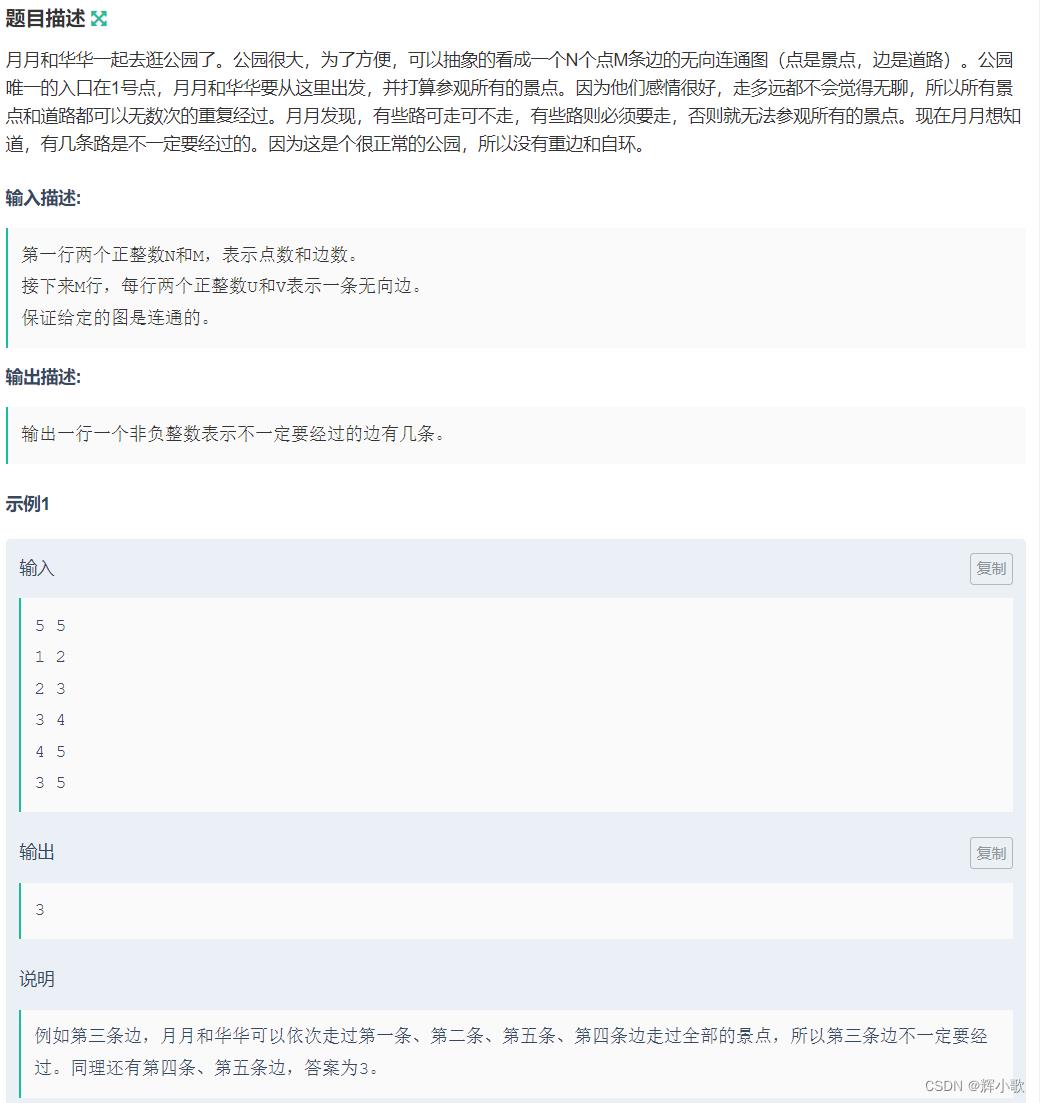
总的数量-桥的数量==答案
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
const int M=1e5*6+10;
int h[N],e[M],ne[M],idx;
int dfn[N],low[N],timestep;
bool bridge[M];
int n,m;
void add(int a,int b)
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
void tarjan(int u,int fa)
dfn[u]=low[u]=++timestep;
for(int i=h[u];i!=-1;i=ne[i])
int j=e[i];
if(!dfn[j])
tarjan(j,i);
low[u]=min(low[u],low[j]);
if(dfn[u]<low[j])
bridge[i]=bridge[i^1]=true;
else if(i!=(fa^1)) low[u]=min(low[u],dfn[j]);
int main(void)
cin>>n>>m;
memset(h,-1,sizeof h);
while(m--)
int a,b; scanf("%d%d",&a,&b);
add(a,b),add(b,a);
tarjan(1,-1);
int cnt=0;
for(int i=0;i<idx;i++) if(!bridge