1决策树理论知识详解与sklearn实践

Posted 2022-05-02 zstar-_

看过我数学建模专栏的读者应该知道，我从去年开始就计划写这专栏，但由于各种原因，一直无暇实施计划。而从本篇开始，这个专栏将开始填坑。每篇博文会采用理论+实践的形式，试图用sklearn这个强大的工具包来实现机器学习中的一些经典算法。
本篇的核心算法是决策树。

决策树理论

首先看决策树的相关理论，在我看过的一些资料中，李航老师的《统计机器学习》这部分写得最全面，因此下面的内容主要参考了这本书，但顺序我做了一些更改，改成了决策树理论建立的顺序，以便读者能够更容易看懂。

决策树基本概念

说到“树”，可能会联系到数据结构中的树概念。没错，决策树基本结构就是数据结构中的树状图。看下图两个简单例子：

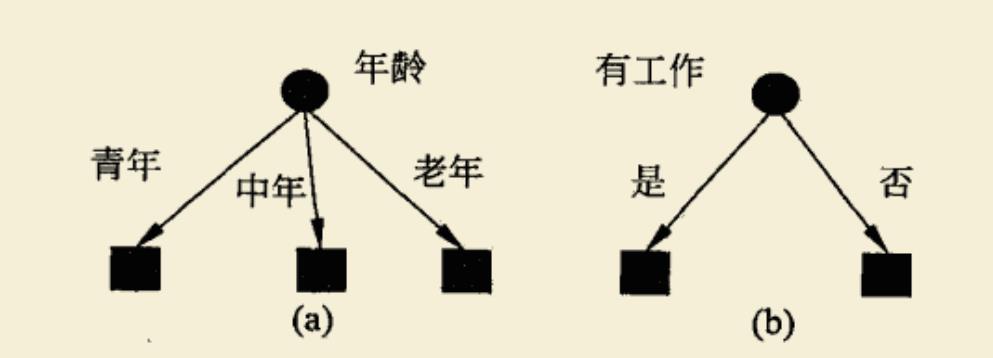
一个根节点可根据条件分裂成不同的子节点，银行业就常用这个模型来根据用户信用来判断是否贷款。
决策树既可以做分类，又可以做回归。但通常来说，做分类的情况更多。
基本模型有了，那么这些指标如何进行排布？又依据什么来分类？这就要引出下面的数学指标。

经验熵

先看一个数理概念——经验熵。
熵原本是物理上的一个概念，用来描述事物的混乱程度。而经验熵(在信息论里也叫信息熵)，用来衡量事物的不确定程度。
我们假设X为一维随机变量，它的概率分布满足
$$P\left(X=x_i\right)=p_i,i=1,2,\dots ,n$$
则X的经验熵为
$$H(X)=-\sum _{i=1}^n{p}_i\log p_i$$
为了探究经验熵的实际意义，我们考虑一种最简单的概率分布，即伯努利分布(0-1)分布。
设X=1的概率为p，则X的分布为
$$P(X=1)=p,P(X=0)=1-p,0⩽p⩽1$$
经验熵H§为
$$H(p)=-p{\log }_{2}p-(1-p){\log }_2(1-p)$$
绘制经验熵H§随概率p变化曲线如下图所示。

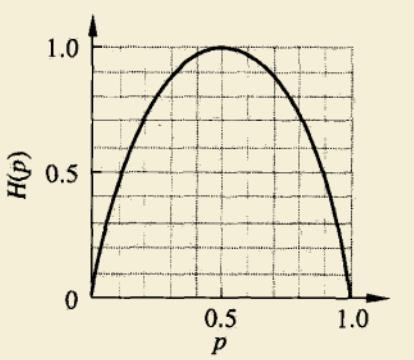
当p=0或p=1时，H§=0，此时X的取值是确定的，没有随机性。
当p=0.5时，H§=1,此时X的取值最随机，X=0或X=1的概率各占一半。
因此，我们可以认识到经验熵的实际意义是衡量不确定性，熵越大则不确定性越大。
这里顺便提一下熵概念的引出和信息论中的信息量有关，熵的定义式实际上就是 概率*信息量。

条件熵

上面是最简单的一种情况，如果我们把随机变量的个数增加成两个，就可以引出条件熵的概念。
设随机变量(X,Y)的联合概率分布为
$$P\left(X=x_i,Y=y_j\right)=p_{ij},i=1,2,\cdots ,n;j=1,2,\cdots ,m$$
则条件熵H(Y|X)为
$$H(Y\mid X)=\sum _{i=1}^n{p}_{i}H\left(Y\mid X=x_i\right)$$
条件熵H(Y|X)表示在X的条件下Y的不确定性。
注：对于概率为0的情况，规定0log0=0。

信息增益

有了上面两个概念之后，我们再将其进行相减，这样就得到了新的概念——信息增益。
$$g(D,A)=H(D)-H(D\mid A)$$
信息增益g(D, A)表示因特征A而导致数据集D分类不确定性减少的程度。
听起来很绕？那翻译一下。我们的目标是让数据集D尽可能分开，即让分类不确定性最小，那应该怎么挑选特征最好，自然是先挑那些最“显著”的特征，这个显著的衡量标准就是信息增益。

下面看了例子，以便对公式的理解更深刻。
首先给定数据集D，如下图所示。

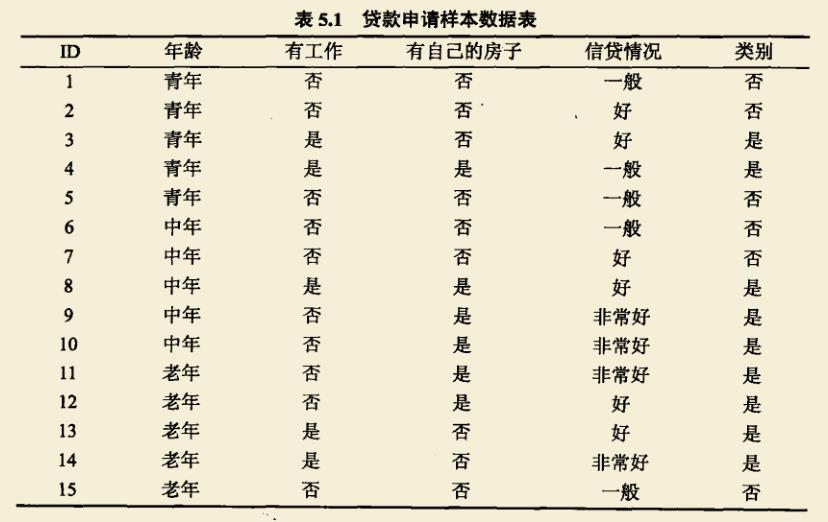
这里有年龄、有工作、有自己的房子、信贷情况四个特征，我们需要根据信息增益来选择最优的一个特征。
套用上面的公式，可以计算出下列数据。


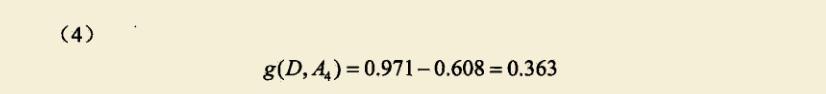
比较四个特征的信息增益，发现g(D,A3)最大，因此有自己的房子是最优特征。

ID3算法

通过上面的例子，我们已经能够通过信息增益来筛选出最优特征。那么，如果不断得进行特征筛选，那就能构成一棵决策树。这就是ID3算法的思想。

ID3算法描述： 从根节点开始，对节点计算所有可能的特征的信息增益，选择信息增益值最大的特征作为节点的划分特征； 由该特征的不同取值建立子节点； 再对子节点递归地调用以上方法，构建决策树；直到所有特征的信息增益都很小或者没有特征可以选择为止，得到最终的决策树。

还是拿上面的房贷例子来说，上面我们只进行了一步划分，根据是否有房子特征来划分出有房者能够发放贷款，但对于无房者来说，都全部拒绝吗？显然不是，我们还需要根据其它的特征进行进一步划分。而这部分需要划分的数据集记为D2。在这个数据集中，就可以根据剩下的特征再次进行划分，同样计算信息增益：

g(D2,A2)最大，因此选择A2特征进行下一步分裂，这样就可以得到决策树。

但ID3算法存在一个缺点是，当数据量过大时，它依旧会把每个叶子节点分出来，而不存在剪枝策略，这就导致运算缓慢。而剪枝策略就是下一个算法C4.5对ID3的优化之一。

信息增益比

在进入C4.5算法之前，需要引入一个新的概念：信息增益比。
$$g_R(D,A)=\frac{g(D,A)}{H(D)}$$
理解起来也很简单，就是把信息增益和信息熵相除。
为什么要引入这个概念呢？因为之前我们使用信息增益来进行特征选择时，经验熵越大，信息增益值也会偏大，两者进行相比，则可以进行校正，有了这个概念之后，就可以自然得进入到C4.5算法。

C4.5算法

看名字也知道，这个算法一定是在ID3之后的。相比于ID3，C4.5做了两个改进：
1、划分标准改为信息增益比
2、引入剪枝策略

下面介绍剪枝策略

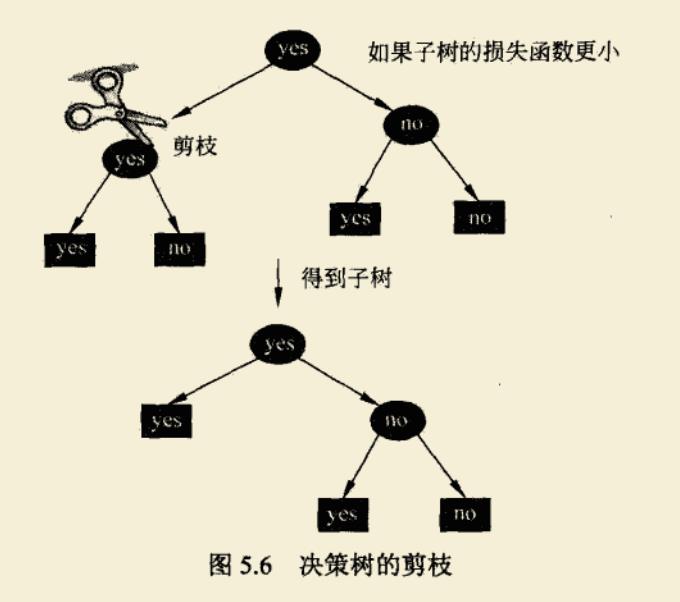
这张图能明确得表示了剪枝概念，即需要通过剪除一些分支来降低整体的复杂度，这里还需要引入一个新的概念–损失函数。
$$C_{\alpha }(T)=\sum _{t=1}^{|T|}{N}_t{H}_t(T)+\alpha |T|$$
式中，|T|表示树T的叶结点数量，$H_t(T)$表示叶结点t上的经验熵
如果我们把第一项记作C(T)，代入经验熵的定义式，有
$$C(T)=\sum _{t=1}^{|T|}{N}_t{H}_t(T)=-\sum _{t=1}^{|T|}\sum _{k=1}^K{N}_{tk}\log \frac{N_{tk}}{N_t}$$
这样，损失函数就可以简写为
$$C_{\alpha }(T)=C(T)+\alpha |T|$$
如果学过机器学习，就会发现这个式子和正则化的损失函数非常类似。
C(T)表示模型对训练数据的预测误差，即模型和训练数据的拟合程度，|T|表示模型复杂度，参数$\alpha$则控制了拟合程度和复杂度的均衡。通常来说，模型拟合程度越高，复杂度也越高，这就产生了过拟合现象，这时候需要正则化来进行缓解。这里的$\alpha$就控制了正则化的程度。

有了这个概念后，就可以判断什么时候应该采用剪枝。

剪枝是个不断从叶结点向上递归迭代的过程，当全部剪完后，就能得到最终的决策树。

CART算法

上面的ID3和C4.5都只适用于分类的场景。CART算法则进行了进一步的拓展，既可以回归也可以分类。同样，CART算法和C4.5算法过程类似，包含决策树生成，决策树剪枝。

回归树的生成

回归树的生成采用平方误差最小化准则，因此回归树通常称为最小二乘回归树。
算法流程见图，不作详细分析。

分类树的生成/基尼指数

上面提到ID3的分类指标用了信息增益，C4.5用了信息增益率，这里的CART也做了修改，用了基尼指数。
基尼指数的定义：
假设有K个类，样本点属于第k类的概率为$p_{[机器学习python实践]Sklearn实现集成}$

sklearn实践：决策树

[机器学习与scikit-learn-15]：算法-决策树-分类问题代码详解

sklearn2.分类决策树实践——Titanic数据集

详解决策树-交叉验证菜菜的sklearn课堂笔记

详解决策树-分类树菜菜的sklearn课堂笔记