C++中的cmath头文件

Posted 2023-03-19

问问各位大侠，在VC中#include<cmath>头文件在什么情况下调用，和具体有什么要求，谢谢了。
小弟不胜感激！！！

math.h是C语言的头文件。其实在C++中用math.h也是可以的，C++是兼容C的。
不过推荐的是使用#include，而且必须声明在std命名空间：using namespace std；其中的函数和使用方法几乎完全相同。
VC里面是math.h，cmath是c++标准风格的头文件，位于std命名空间，用法和math.h差不多，都是包含一些常见的数学函数，比如平方、正余弦等等 参考技术A 按命名规则，cmath 应该是math.h的C++版，什么时候用math.h就什么时候用cmath替代。一般是要用到常用的数学函数时调用，比如abs(),sin()等。 参考技术B VC里面是math.h，cmath是c++标准风格的头文件，位于std命名空间，用法和math.h差不多，都是包含一些常见的数学函数，比如平方、正余弦等等
具体参考：http://www.ggv.com.cn/forum/clib/clib.html本回答被提问者采纳 参考技术C 回答

1. ceil()向上取整2. round()四舍五入取整，3. floor()向下取整且以上所有参数必须为double型4.取整与取余double modf (double,double*); 将参数的整数部分通过指针回传，返回小数部分double fmod (double,double); 返回两参数相除的余数绝对值1. int abs(int );求整型的绝对值2. double fabs (double);求实型的绝对值3. double cabs(complex);求复数的绝对值三角函数1、 三角函数double sin(double);正弦double cos(double);余弦double tan(double);正切2 、反三角函数double asin (double); 结果介于[-PI/2,PI/2]double acos (double); 结果介于[0,PI]double atan (double); 反正切（主值），结果介于[-PI/2,PI/2]double atan2 (double,double); 反正切（整圆值），结果介于[-PI,PI]3 、双曲三角函数double sinh (double);double cosh (double);double tanh (double);没有现成的cot三角函数，可以使用tan(PI/2-x)来实现指数与对数double frexp(double value,int exp);这是一个将value值拆分成小数部分f和（以2为底的）指数部分exp，并返回小数部分f，即f2^exp。其中f取值在0.5~1.0范围或者0。double ldexp(double x,int exp);这个函数刚好跟上面那个frexp函数功能相反，它的返回值是x*2^expdouble modf(double value,double *iptr);拆分value值，返回它的小数部分，iptr指向整数部分。double log (double); 以e为底的对数double log10 (double);以10为底的对数double pow(double x,double y);计算x的y次幂fl

小白学习C++ 教程十九C++ 中的＜cmath＞ 数学函数和 ＜random＞随机数

@Author：Runsen

C++提供了大量的数学函数，可以直接在程序中使用。

cmath

作为 C 语言的一个子集，C++ 从 C 的 math.h 头文件中派生出大部分这些数学函数。

在 C++ 中，数学函数包含在头文件<cmath> 中。

下面列出了 C++ 中的重要数学函数及和示例

1	cos	cout<< cos ( 60.0 * PI / 180.0 );
2	sin	con ( 60.0 * PI / 180.0 );
3	tan	out<< tan ( 45.0 * PI / 180.0 )
4	acos	double param = 0.5; cout<< acos (param) * 180.0 / PI;
5	asin	cout<< asin (param) * 180.0 / PI; 31.4159
6	atan	cout<< atan (param) * 180.0 / PI;
7	pow	cout<<”2^3 = “<< pow(2,3);
8	sqrt	cout<< sqrt(49);
9	ceil	cout<< ceil(3.8);
10	floor	cout<< floor(2.3);
11	fmod	cout<< fmod(5.3,2); 1.3
12	trunc	cout<< trunc(2.3); 2
13	round	cout<< round(4.6); 5
14	remainder	cout<< remainder(18.5 ,4.2); 1.7
15	fmax	cout<< fmax(100.0,1.0); 100
16	fmin	cout<< fmin(100.0,1.0); 1
17	fdim	cout<< fdim(2.0,1.0); 1
18	fabs	cout<< fabs(3.1416); 3.1416
19	abs	cout<< abs(3.1416); 3.1416
20	exp	cout<< exp(5.0); 148.413
21	log	cout<< log(5); 1.60944
22	log10	cout<< log10(5);

#include <iostream>
#include <cmath>
using namespace std;
int main()
{
	int PI = 3.142;
	cout << "cos(60) = " << cos(60.0 * PI / 180.0) << endl;
	cout << "sin(60) = " << sin(60.0 * PI / 180.0) << endl;
	cout << "tan(45) = " << tan(45.0 * PI / 180.0) << endl;
	cout << "acos(0.5) = " << acos(0.5) * 180.0 / PI << endl;
	cout << "asin(0.5) = " << asin(0.5) * 180.0 / PI << endl;
	cout << "atan(1.0) = " << atan(1.0) * 180.0 / PI << endl;
	cout << "2^3 = " << pow(2, 3) << endl;
	cout << "sqrt(49) = " << sqrt(49) << endl;
	cout << "ceil(3.8) = " << ceil(3.8) << endl;
	cout << "floor(2.3) = " << floor(2.3) << endl;
	cout << "fmod(5.3,2) = " << fmod(5.3, 2) << endl;
	cout << "trunc(5.3,2) = " << trunc(2.3) << endl;
	cout << "round(4.6) = " << round(4.6) << endl;
	cout << "remainder(18.5,4.2) = " << remainder(18.5, 4.2) << endl;
	cout << "fmax(100.0,1.0) = " << fmax(100.0, 1.0) << endl;
	cout << "fmin(100.0,1.0) = " << fmin(100.0, 1.0) << endl;
	cout << "fdim(2.0,1.0) = " << fdim(2.0, 1.0) << endl;
	cout << "fabs(3.1416) = " << fabs(3.1416) << endl;
	cout << "abs(3.1416) = " << abs(3.1416) << endl;
	cout << "log(5) = " << log(5) << endl;
	cout << "exp(5.0) = " << exp(5.0) << endl;
	cout << "log10(5) = " << log10(5) << endl;
	return 0;
}

输出如下

cos(60) = 0.540302
sin(60) = 0.841471
tan(45) = 0.931596
acos(0.5) = 62.8319
asin(0.5) = 31.4159
atan(1.0) = 47.1239
2^3 = 8
sqrt(49) = 7
ceil(3.8) = 4
floor(2.3) = 2
fmod(5.3,2) = 1.3
trunc(5.3,2) = 2
round(4.6) = 5
remainder(18.5,4.2) = 1.7
fmax(100.0,1.0) = 100
fmin(100.0,1.0) = 1
fdim(2.0,1.0) = 1
fabs(3.1416) = 3.1416
abs(3.1416) = 3.1416
log(5) = 1.60944
exp(5.0) = 148.413
log10(5) = 0.69897

random

在中定义了两个类用于实现随机数：

• 随机数引擎类：生成随机数
• 随机数分布类：生成满足指定分布的随机数

生成随机数

• random_device：它是真正的随机数生成器。
• operator()：它返回一个新的随机数。
• min：它返回成员 operator() 返回的最小值，对于 random_device 始终为零。
• max：它返回成员 operator() 返回的最大值。

#include <iostream>
#include <random>
using namespace std;

int main()
{
    random_device example;
    cout << "default random_device:" << endl;
    cout << "minimum: " << example.min() << endl;
    cout << "maximum: " << example.max() << endl;
    cout << "entropy: " << example.entropy() << endl;
    cout << "a random number: " << example() << endl;

    return 0;
}

输出如下

random_device:
minimum: 0
maximum: 4294967295
entropy: 32
a random number: 773368156

生成满足指定分布的随机数

均匀分布

uniform_int_distribution：它产生随机整数值 i，它们均匀分布在闭区间 [a,b] 上，由以下概率质量函数描述：

• operator()：生成根据概率函数分布的随机数。
• min：它返回operator()返回的值范围的最大下限，这是uniform_int_distribution的分布参数’a’。
• max：它返回operator()返回的值范围的最小上限，这是uniform_int_distribution的分布参数’b’。

#include <iostream>
#include <random>
using namespace std;

// Driver program
int main()
{

    // random generator engine 
    unsigned s = 2;

    // The random number generator
    default_random_engine generator(s);

    uniform_int_distribution<int> distribution(1, 10);
    cout << "Some random numbers between 1 and 10";
    for (int i = 0; i < 10;i++)
        cout << distribution(generator) << endl;

    cout << endl;

    return 0;
}

uniform_real_distribution：是产生浮点值的随机数分布，由以下概率密度函数描述：

#include <iostream>
#include <random>
using namespace std;

int main()
{

    unsigned s = 2;

    // The random number generator
    default_random_engine generator(s);

    uniform_real_distribution<float> distribution(1, 10);
    cout << "Random numbers between 1 and 10";
    for (int i = 0; i < 10; ++i)
        cout << distribution(generator) << endl;

    cout << endl;

    return 0;
}

二项式分布

binomial_distribution：它是根据二项式离散分布产生整数的随机数分布，由这个概率质量函数给出：

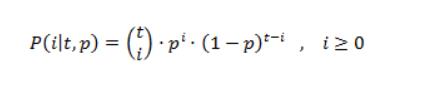
#include <iostream>
#include <random>
#include <chrono>

using namespace std;

int main()
{

    unsigned seed = chrono::system_clock::now().time_since_epoch().count();
    default_random_engine generator(seed);

    binomial_distribution<int> distribution(15, 0.4);

    cout << "some binomial results (t=15, p=0.4): ";
    for (int i = 0; i < 15; ++i)
    {

        // Use of operator()
        cout << distribution(generator) << " ";
    }
    cout << endl;
    return 0;
}

geometry_distribution：它是一种随机数分布，根据几何离散分布生成整数，由以下概率质量函数给出：

在这里插入图片描述

rand

C++ 库有一个名为 rand() 的函数，每次调用该函数都将返回一个非负整数。要使用 rand() 函数，以下是其用法示例：

#include <iostream>
using namespace std;

int main() {
    for (int i = 0; i < 100; i++) {
        cout << rand() << ' ';
    }
    return 0;
}