数字图像处理的数学变化 线性点运算分段线性点运算非线性点运算阈值化运算

Posted 2022-04-29 nanke_yh

目录

1、引言

2、点运算

2.1线性点运算

2.2分段线性点运算

2.3非线性点运算

3、灰度阈值化

---

1、引言

        图像的数学变换的特点在于其有精确的数学背景，是许多图像处理技术的基础。在这些变换中，一种是在空间域上进行的，这些变换根据处理操作的特点，可以分为图像的代数运算和几何运算，它们都是利用对输入图像进行加工而得到输出图像。另一种重要的数学变换则是将原定义在图像空间的图像以某种形式转换到另外一些空间，并利用输入图像在这些空间的特有性质有效而快速地对图像进行处理和分析。最典型的变换有离散傅立叶变换，它把空域中的图像信号看作二维时间序列，将其变换到频率域来分析图像的频谱特性。

        空域变换有如加法、减法等的代数变换，也有如旋转、拉伸等的几何变换；频域变换除了傅立叶变换外，常用的非空域的变换还有离散余弦变换、PCA变换等等。无论是在空域中的数学变换还是频域中的数学变换，它们在图像分析、滤波、增强、压缩等处理中都有着非常典型而重要的应用。

2、点运算

        像素作为数字图像空间域上操作的基本单元，像素点运算是空间域数字图像处理的基本。点运算是一种像素的逐点运算，它与相邻的像素之间没有运算关系，点运算不会改变图像内像素点之间的空间位置关系。点运算主要分为线性点运算、分段线性点运算和非线性点运算。

2.1线性点运算

        像素点线性运算数学公式：

         其中，a、b为常数。

        这个很好理解，即对输入的某个数字图像像素通过乘以a或者加b改变输入的原有像素值，再将其值输出就完成了这一个像素的简单数字变换了。然后将之遍历全部图像即完成了整幅图像的线性变换。

        这里主要可以得到以下的一些结论：当a=1，b=0时，输入输出图像恒等；当a<0时，黑白翻转；当|a|>1时，增加对比度；当|a|<1时，减少对比度；当b>0时，增加亮度；当b<0时，减小亮度。

        以某一种情况（a=-1，b=255来实现黑白翻转）测试：

for (int row = 0;row < height;row++)         for (int col = 0;col < width;col++)                          double t = ptImage[row * width + col];                 double temp = a * t + b;                 if (temp>ColorLen-1)                                          temp = ColorLen-1;                                  if (temp < 0)                                          temp = 0;                                  ptImage[row * width + col] = (ImgTyp)(temp);
输入图像	输出图像

2.2分段线性点运算

        分段线性点运算是线性点运算中的一个具体应用，主要是通过划分灰度区间将图像像素值进行区别处理。可以做到将感兴趣区域的灰度范围线性扩展，相对抑制不感兴趣的灰度区域。

//对灰度值进行分段线性处理，a=0.5，b=-10，min=80，max=200 if (t>min && t<max)         temp = a * t + b; else         temp = t;
输入图像	输出图像

        如上所示的三分段案例，因为是测试选择的参数就比较粗糙，抑制中间部分的亮度，两端不变，但是可见输出图像存在像素值突变的情况，整体看起来不是很顺滑存在斑块，在实际的数字图像处理中需要根据情况确定参数且需要使得图像灰度值连续。

2.3非线性点运算

        在线性运算中，像素点间值得变化是一种比例变化，但是在实际中，需要对图像得某个特征进行放大或缩小，特别是在图像增强得过程中，为了消除图像失真，非线性运算显示了其重要性。幂运算、指数运算、对数运算是最简单得非线性映射算法。

        像素点非线性运算的数学通式为：

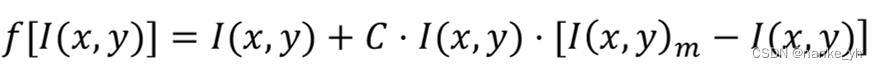
        其中，C为常量，I(x,y)m为最大值。

        可以发现：当C<0时，增强中间部分亮度，当C>0时，减小中间部分亮度。在数学层面直观表现有：

        但是，从图像色阶层面考虑，在实际的图像处理中往往需要对上面公式进行变化，不然很容易越界导致色彩单一。为此，通常的非线性函数灰度变化公式为：

f[I(x,y)] = I(x,y) + C*I(x,y)*[I(x,y)m - I(x,y)]/I(x,y)m

        基于此进行测试有：

//对像素值进行非线性点运算，C=0.8，ColorLen=256 double temp = t + C * t * (ColorLen-1 - t)/(ColorLen-1);
输入图像	输出图像

3、灰度阈值化

        阈值又称为临界值，它的目的是确定出一个范围，然后这个范围内的部分使用同一种方法处理，而阈值之外的部分则使用还有一种处理方法或保持原样。经常使用的包含产生二值图：当x<T时y=0，当x>=T时y=255（当中T是阈值）。阈值变换在生物学上的应用比较广泛，经常使用语细胞图像切割等。

//对图像进行二值化，thresh=128，ColorLen=256 double temp = 0.0; if (t>thresh)         temp = ColorLen-1; else         temp = 0;
输入图像	输出图像

        基础的原理和操作实现和整理了一下，如果文中有什么错误，希望大家在评论中指出来，谢谢！