区块链与密码学第5-4讲：详解常用哈希函数

Posted 2022-04-27 Dig Quant

【本课堂内容全部选编自PlatON首席密码学家、武汉大学国家网络安全学院教授、博士生导师何德彪教授的《区块链与密码学》授课讲义、教材及互联网，版权归属其原作者所有，如有侵权请立即与我们联系，我们将及时处理。】

5.4.1 Keccak算法简介

美国国家标准与技术研究院(National Institute of Standards and Technology，NIST)于2007年公开征集SHA-3，要求：

能够直接替代SHA-2，这要求SHA--3必须也能够产生224，256，384，512比特的哈希值。

保持SHA-2的在线处理能力，这要求SHA-33必须能处理小的数据块(如512或1024比特)。

安全性：能够抵抗原像和碰撞攻击的能力，能够抵抗已有的或潜在的对于SHA-2的攻击。

效率：可在各种硬件平台上的实现，且是高效的和存储节省的。

灵活性：可设置可选参数以提供安全性与效率折中的选择，便于并行计算等。

2008年10月，有64个算法正式向NIST提交了方案，经过初步评价，共有51个算法进入第一轮评估，主要对算法的安全性、消耗、和实现特点等进行分析。

2009年7月24日宣布，其中14个算法通过第一轮评审进入第二轮；2010年12月9日宣布，其中5个算法(JH、Grstl、Blake、Keccak和Skein)通过第二轮评审进入第三轮。

2012年10月2日NIST公布了最终的优胜者，它就是由意法半导体公司的Guido Bertoai Bertoai、Jean Daemen Daemen、Gilles Van Assche Assche与恩智半导体公司的Micha Michaëël Peeters 联合设计的Keccak算法。

SHA-3成为NIST的新哈希函数标准算法(FIPS PUB 180--5)，Keccak算法的分析与实现详见：https://keccak.team/index.html

SHA-3的结构仍属于Merkle提出的迭代型哈希函数结。最大的创新点是采用了一种被称为海绵结构的新的迭代结构.。海绵结构又称为海绵函数。

在海绵函数中，输入数据被分为固定长度的数据分组。每个分组逐次作为迭代的输入，同时上轮迭代的输出也反馈至下轮的迭代中，最终产生输出哈希值。

海绵函数允许输入长度和输出长度都可变，具有灵活的性，能够用于设计哈希函数(固定输出长度)、伪随机数发生器，以及其他密码函数。

5.4.2 Keccak算法描述

其输入数据没有长度限制，输出哈希值的比特长度分为：224，256，384，512。

符号与函数

Keccak算法使用以下符号与函数：

符号

r：比特率(比特 rate)，其值为每个输入块的长度

c：容量(capacity)，其长度为输出长度的两倍

b：向量的长度，b=r+c，而b的值依赖于指数I，即b=25×2I  

Keccak算法的参数定义

函数

Keccak算法用到了以下5个函数：θ(theta)、ρ(rho)、π(pi)、χ(chi)、ι(iota)

算法描述

Keccak算法对数据进行填充，然后迭代压缩生成哈希值。

填充

对数据填充的目的是使填充后的数据长度为r的整数倍.因为迭代压缩是对r位数据块进行的，如果数据的长度不是r的整数倍，最后一块数据将是短块，这将无法处理。

设消息m长度为l比特。首先将比特“1”添加到m的末尾，再添加k个“0”，其中，k是满足下式的最小非负整数：l+1+k=r-1modr；

然后再添加比特“1”添加到末尾. 填充后的消息m的比特长度一定为r的倍数。

以算法Keccak-256，信息“abc”为例显示补位的过程. a, b, c对应的ASCII码分别是97, 98, 99；于是原始信息的二进制编码为：01100001 01100010 01100011。此时r  = 1088。

① 补一个“1” ：0110000101100010 01100011 1

② 补1062个“0”：

01100001 01100010 01100011 10000000 00000000 … 00000000

③ 补一个“1” ，得到1088比特的数据：

整体描述

Keccak算法采用海绵结构(Sponge Construction)，在预处理(padding并分成大小相同的块)后，海绵结构主要分成两部分：

吸入阶段(Absorbing Phase)：将块xi传入算法并处理。

挤出阶段(Squeezing Phase)：产生一个固定长度的输出。

Keccak算法的整体结构如下图：

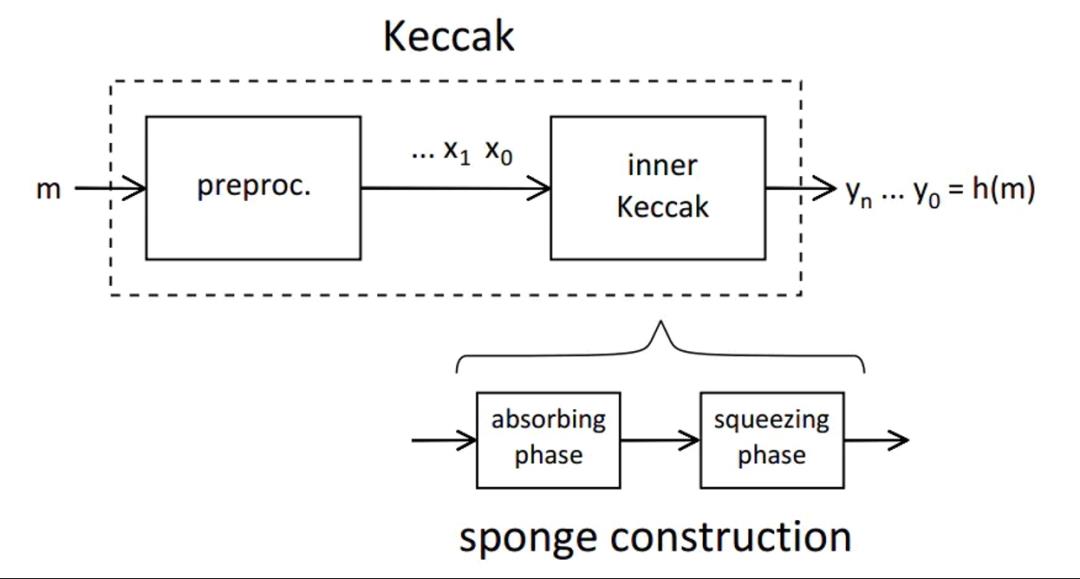
Keccak算法的整体运算示意图

吸入与挤出阶段

给定输入串x，首先对x做padding，使其长度能被r整除，将padding后分割成长度为r的块，即x=x0|| x1|| x2||...|| xt-1 。然后执行以下吸入阶段和挤出阶段：

1.初始化一个长度为r+c比特的全零向量。

2.输入块xi，将xi和向量的前r个比特做异或运算，然后输入到f函数中处理。

3.重复上一步，直至处理完x中的每个块。

4.输出长为r的块作为y0，并将向量输入到f函数中处理，输出y1，以此类推，得到的哈希序列即为y= y0||y1||y2||...||yu。在Keccak-224/256/384/512中，只需要在y0中取出前224/ 256/ 384/ 512位即可。

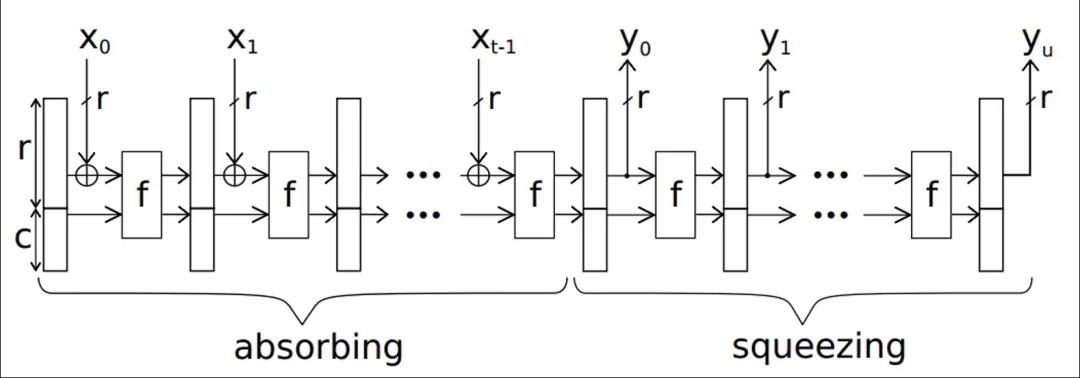
 Keccak算法的吸入阶段和挤出阶段示意图

压缩函数

压缩函数f是Keccak算法的核心，它包含nr轮。

nr的取值与我们之前计算b时用到的指数I (b=25×2I)有关，具体地，nr=12+2*I.Keccak-224/256/384/512中，取I=6，因此nr=24。

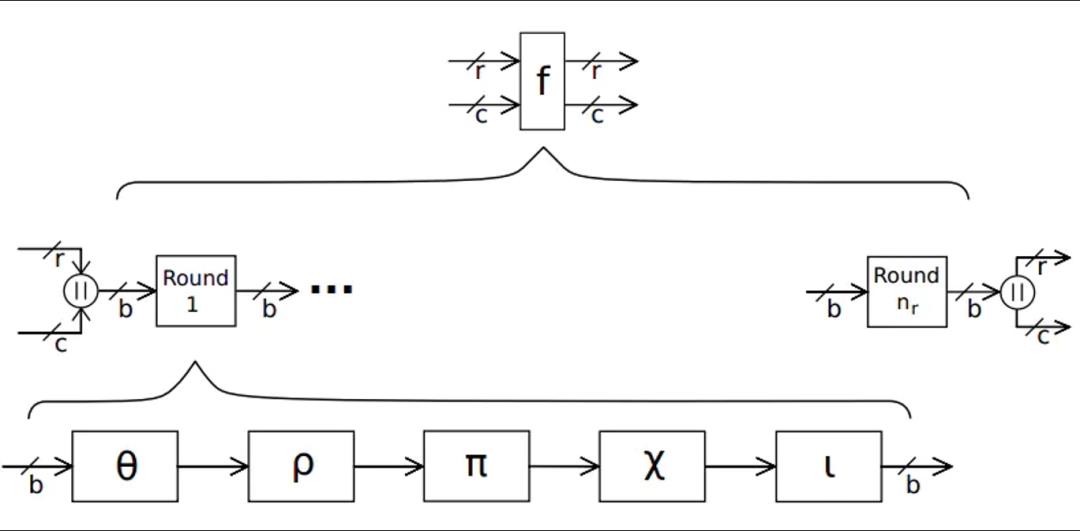
在每一轮中，要以此执行五步，即θ(theta)、ρ(rho)、π(pi)、χ(chi)、ι(iota)。

在处理过程中，我们把b=1600个比特排列成一个5*5*w的三维数组，其中w=2I=64比特，如右图所示：

 Keccak算法的三维数组示意图

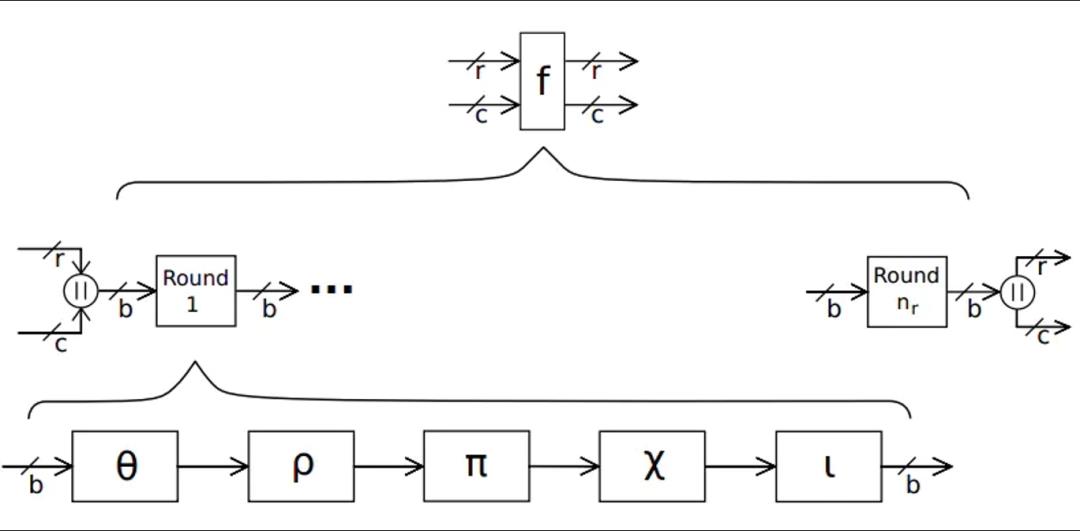
Keccak算法的压缩函数结构示意图

安全性与性能

安全性

可以抵御对哈希函数的所有现有攻击。

到目前为止，没有发现它有严重的安全弱点。

灵活性

可选参数配置，能够适应哈希函数的各种应用。

高效性

设计简单，软硬件实现方便.在效率方面，它是高效的。

尚未广泛应用，需要经过实践检验。

常用的Keccak算法就讲到这里啦，下节课我们将学习常用哈希函数SM3算法，敬请期待！