逻辑回归dome演示

Posted 2022-04-20 Huterox

文章目录

• 前言
• • 逻辑回归能干嘛
  • 评判标准
  • 数据集
  • 训练策略
  • 梯度更新
• 编码

前言

逻辑回归能干嘛

开始之前先明确逻辑回归能干嘛，首先这玩意使用的是梯度下降法来进行修正。整个过程，逻辑回归的过程类似一个小型神经网络。这玩意主要应用于二分类问题。

相关理论请参考：逻辑回归模型详解(Logistic Regression)
这里不做过多的理论探究。

评判标准

这里的话主要还是以实战为主，如何手撸一个超级简单的逻辑回归dome，演示神经网络的工作流程。
这个灵感还是来自与这个大哥：BoyC啊（老卷王：宁可累死也要卷死别人的老狠人！！！）

首先是损失函数。

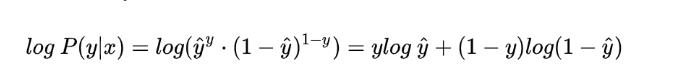
长这样。

其中那个 y^ 是指你的预测值，y 是实际上的值。由于是一个二分类的问题，所以，在对0这个标签拟合计算损失的时候，损失值越接近1越好，拟合 1 标签的时候，越接近0 越好，所以总体的损失值，越接近0.5越好。
这个主要是他们那个理论推导来的，我这里直接说的结论。

然后是预测函数。

在咱们今天的这篇博文的话，我们做的是一个简单的二分类，是有十组数据，我们先看看最后的一个效果吧：

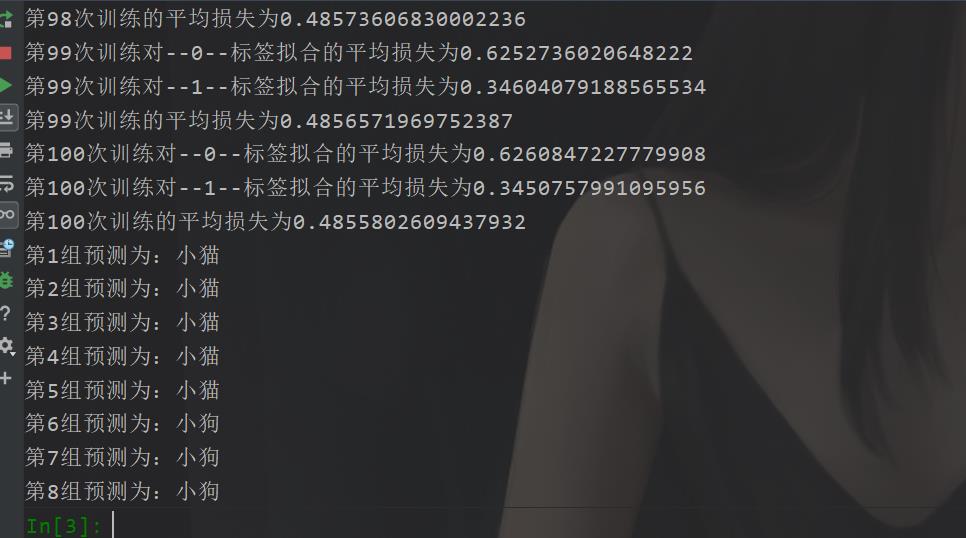
当然这里的话，我的损失计算也还是有点问题的，大体是这样的，你们后面可以考虑优化。

正向函数，在这里的话，叫做网络函数比较合适，是这样的。

def Net(X):
    X = X.T * W
    X = np.sum(X) +B
    X = sigmod(X)
    if(X>=1):
        X = X-0.0001
    elif(X<=0):
        X = X + 0.0001
    return X

这里还要对那个± 0.0001 是因为那个 这里的 sigmod 处理之后，如果某一个值非常接近1或者0的时候，就会被取成1或者0，但是这个是不允许的。只能这样先特殊处理了。
然后整个网络结构是长这个样子的。

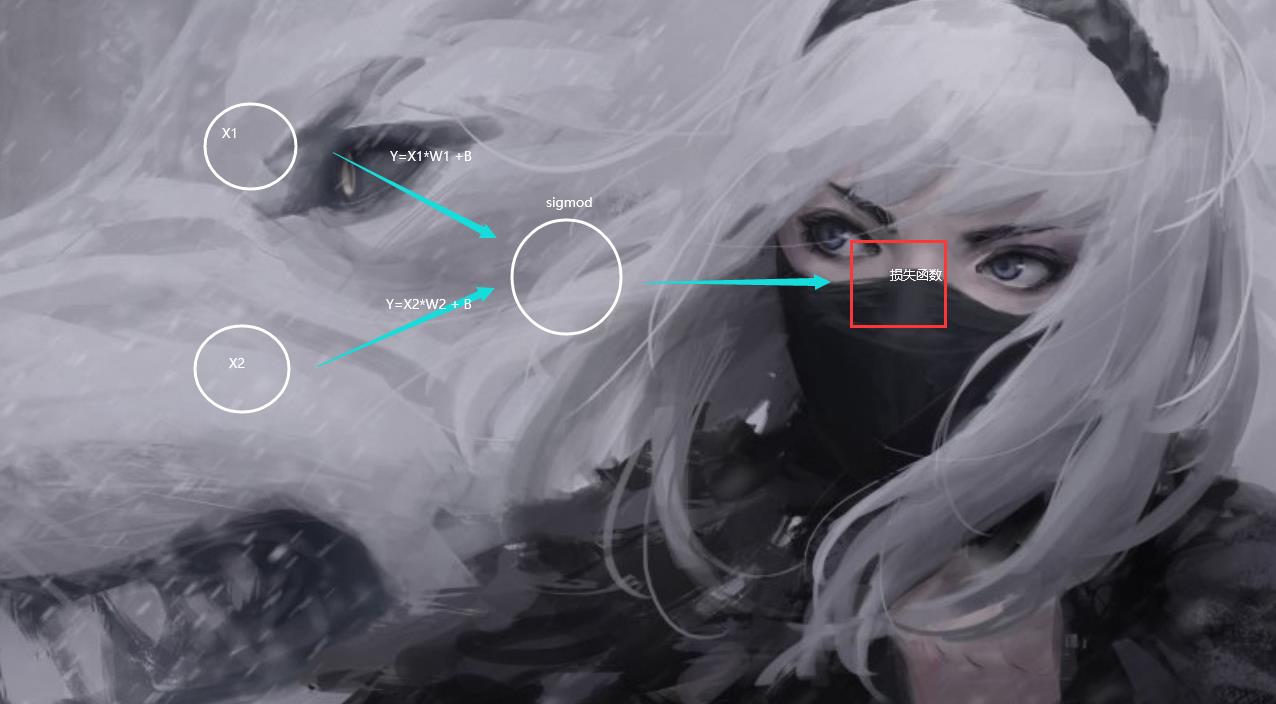
所以你可以知道为什么那个Net函数这样的。

数据集

在我们的这个dome当中的话，我们的这个数据集是这样的。

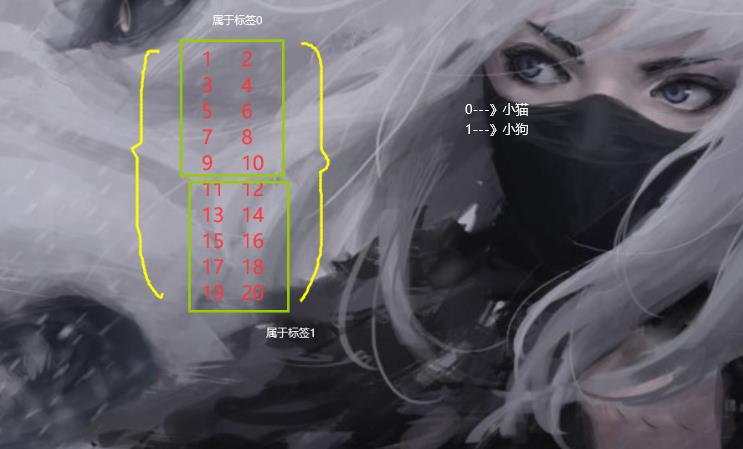
X_train  = np.linspace(1,20,20).reshape((10,2))
classes = ["小猫","小狗"]
Labels = "小猫":0,"小狗":1
Y_train = np.array([Labels["小猫"],Labels["小狗"]])

训练策略

之后咱们来说说咱们的这个训练策略。
首先，咱们的这个数据是一行一行输入进去的，前5组属于0标签，后5组属于1标签。之后，为了模拟这个神经网络的batch_size
所以，我这里还干脆在每一轮训练的时候，每进去5组，5组计算完了之后，我再去进行梯度下降，更新权重，每一次计算，我先把所有的梯度加起来，然后后面求平均值然后去更新。（我们现在模拟的是非常简答的网络结构，对于复杂的，我们就需要单独记录梯度然后去更新，这样如果每进去一组我就更新梯度的话是会浪费很多时间的）

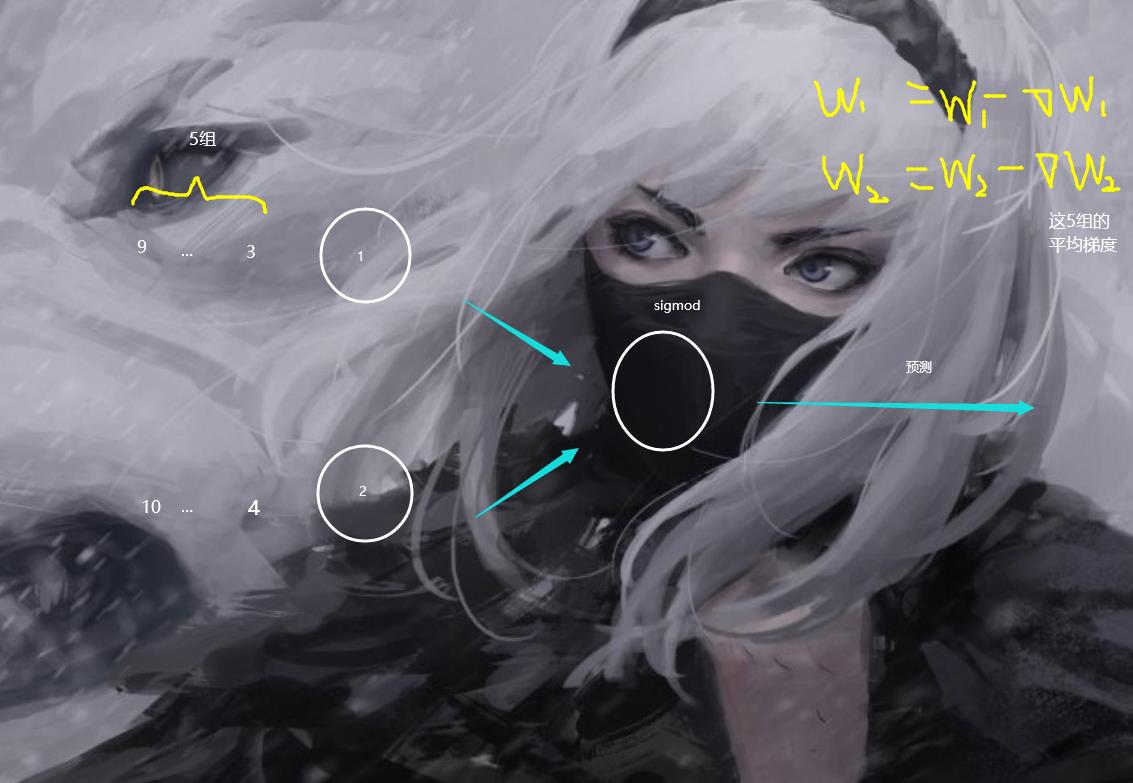
梯度更新

这里的话通过求导，我们最后可以发现这个
W1 的 梯度会等于 （当前预测值-实际值）* 当前对于的X1
然后，这里的话，我们既然使用了矩阵，那么我这里更新的时候，直接使用矩阵更新。

同样的，这个B 的话，就是直接 等于 （当前预测值-实际值）
由于我们 是 5 轮 更新一次嘛，所以都要先求个总和然后取平均值。

编码

前面都说的差不多了，那么我们就可以直接进行编码了。
这里由于使用的是梯度下降法，所以的话，我们这里的学习率就是Lr取0.00025
为什么取那么小，因为这个范围0-1本来就很小，参数变化很敏感，梯度下降嘛，容易出现那么几种情况，要么步子太大了过去了，要么就步子太小在局部出不来了，所以那个Lr其实是不太好设置的，在我们实际使用Pytroch的时候，其实我们使用的优化器的那个Lr是动态更新的。但是咱们这里模拟就不搞那么多花里胡哨的了。而且这个我们这里是100轮训练，那个Lr还是我自己调出来的，实际上做的时候，那个参数是作为超参数自适应的。

import numpy as np
import math
X_train  = np.linspace(1,20,20).reshape((10,2))
classes = ["小猫","小狗"]
Labels = "小猫":0,"小狗":1
Y_train = np.array([Labels["小猫"],Labels["小狗"]])

W = np.random.randint(0,1,(2,1))
#划分，2个特征决定0,1,一共十组，这十组前五组为0，后五组为1
#对1类的拟合，是越接近0越好，对于0类的拟合是越接近1越好，
# 对于损失函数，也就是说，总体的损失函数是越接近0.5越好

B = 0
m = 5
def sigmod(X):
    return 1/(1+np.exp(-X))

def com_grad(X,Y_,Y_T):
    #返回的是一个
    #   w1
    #      的向量
    #   w2
    W_ = (X.T)*(Y_ - Y_T)
    #计算梯度

    return W_

def Net(X):
    X = X.T * W
    X = np.sum(X) +B
    X = sigmod(X)
    if(X>=1):
        X = X-0.0001
    elif(X<=0):
        X = X + 0.0001
    return X

def loss(pred,Y_t):

    loss_ = -Y_t * math.log(pred) - (1-Y_t)*math.log(1-pred)
    return loss_

ecpho = 100
Lr = 0.000025
for e in range(ecpho):
    Y_T = None
    B_run = 0
    Pred_total = 0
    W_Z = np.zeros((2,1)) # m个运算之后的总的W
    Loss_Total = 0

    loss_y1_y2 = 0 #这个是针对那个不同的Y的损失
    for i in range(len(X_train)):
        X_ = X_train[i]
        pred = Net(X_)
        if((i+1)<=5):
            Y_T = Y_train[0]
        else:
            Y_T = Y_train[1]
        loss_now = loss(pred,Y_T)
        Loss_Total+=loss_now
        loss_y1_y2+= loss_now
        w_c = com_grad(X_,pred,Y_T)
        w_c = w_c.reshape(2,1)
        W_Z+=w_c
        B_run+=(pred-Y_T)
        Pred_total +=pred
        if((i+1)%m==0):
            W_Z = W_Z /m
            B = B_run/m
            W = W - W_Z*Lr
            print("第次训练对----标签拟合的平均损失为".format(e + 1,Y_T,loss_y1_y2 / m))
            #我们是每m次更新一次，所以更新完之后都要重新刷新
            B_run = 0
            loss_y1_y2 = 0
            W_Z = np.zeros([2, 1])  # m个运算之后的总的W
    print("第次训练的平均损失为".format(e+1,Loss_Total/10))



# 预测部分，在我们的那个数据里面，前面5个是标签1，后面是0，分别对应不同的类别
inx = 1
for i in X_train:
    P = Net(i)
    if(P<0.5):
        print("第组预测为：".format(inx,classes[0]))
    else:
        print("第组预测为：".format(inx, classes[1]))
    inx+=1

看大上面后面的写法，有没有发现和我先前写的那个HuClassfiy分类器有那么点类似。
最后效果是这样的

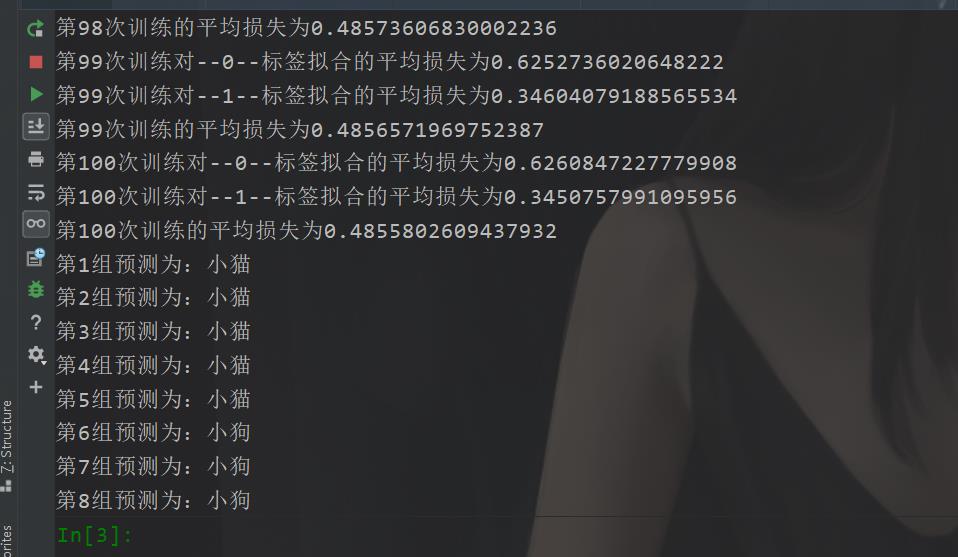
你改一下学习率，例如Lr=0.001

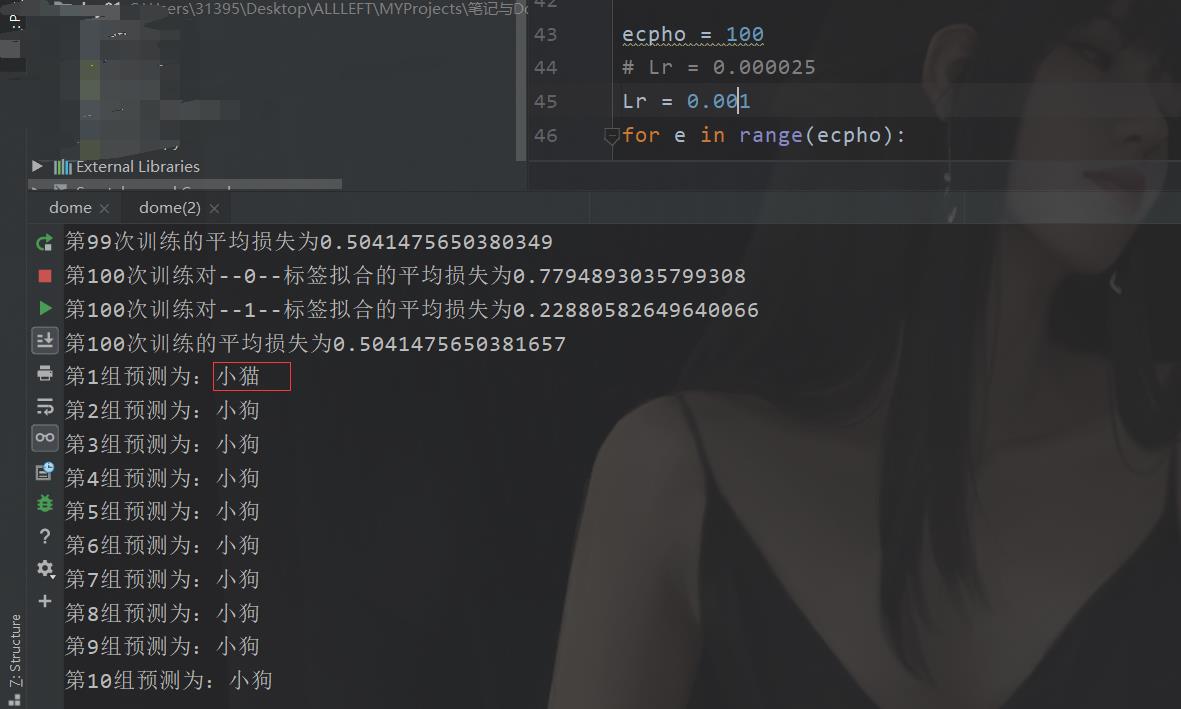
这玩意随缘，当然这个也是多方面因素决定的，有些情况下，有些参数的相关性本来就很差，很难拟合，所以出现这种效果是在所难免的。
在这了的话，我们还是两个特征决定一个类别。就比如那个数据集数子 1,2 共同决定他是0类别，对应的就是小猫。
当然上面那个dome还是有很多不足之处的。