SS-CA-APPLE：什么是留数以及留数定理？

Posted 2022-04-19 卓晴

 

 

§01 数学原理

---

1.1 留数定理

1.1.1 留数定义

  设函数 $f\left(z\right)$ 在区域 $D$ 内解析， $z_0$ 是位于 $D$ 中的 $f\left(z\right)$ 的一个孤立奇点。 $C$ 是 $z_0$ 某个去心邻域中包含 $z_0$ 的一条正向简单闭曲线。定义 $f\left(z\right)$ 在 $z_0$ 处的留数 为： $$\mathrm{Re}s\left[f\left(z\right),z_0\right]=\frac{1}{2\pi i}{\oint }_{C}f\left(z\right)dz$$

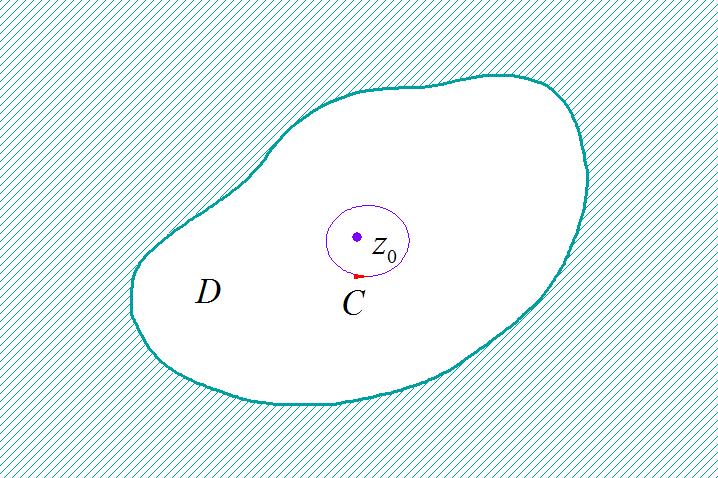
▲ 图1.1.1 解析区域中的孤立奇点

1.1.2 留数定理

  设函数 $f\left(z\right)$ 在区域 $D$ 内除了有限个孤立奇点 $z_1,z_2,\cdots ,z_n$ 外处处解析。 $C$ 是 $D$ 内包围诸奇点的一条正向简单闭曲线，那么 $${\oint }_{C}f\left(z\right)dz=2\pi i\sum _{k=1}^n\mathrm{Re}s\left[f\left(z\right),z_k\right]$$

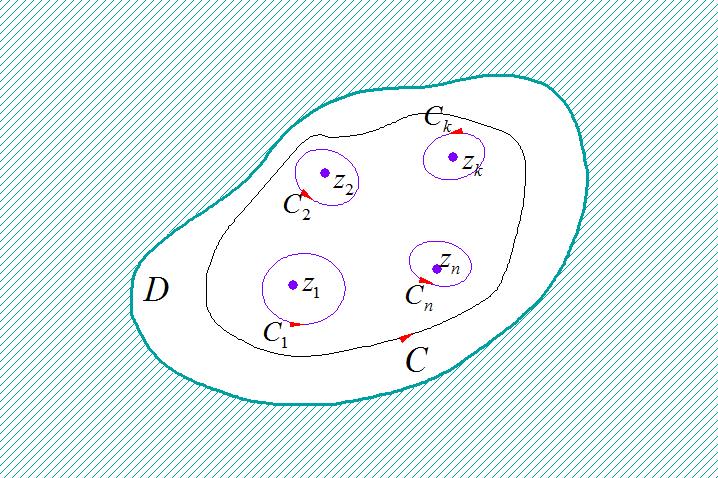
▲ 图1.1.2 留数定理中的区域和孤立奇点

  证明： 【略】

  利用留数定理，求沿封闭曲 $C$ 的积分，就可以转化为求被积函数在 $C$ 中的各个孤立奇点处的留数。

1.2 留数计算规则

1.2.1 规则I

  如果 $z_0$ 为 $f\left(z\right)$ 的一级极点，那么 $$\mathrm{Re}s\left[f\left(z\right),z_0\right]=\underset{z\to z_0}{\lim }\left(z-z_0\right)f\left(z\right)$$

1.2.2 规则II

  如果 $z_0$ 是 $f\left(z\right)$ 的 $m$ 级极点，那么 $$\mathrm{Re}s\left[f\left(z\right),z_0\right]=\frac{1}{\left(m-1\right)!}\underset{z\to z_0}{\lim }\underset{d{z}^{m-1}}{}$$

z域的留数定理和s域的留数定理有啥区别

用Matlab进行部分分式展开

一道拉普拉斯逆变换练习题和对应的数值计算方法

SS-CA-APPLE：什么是复变函数？

SS-CA-APPLE：为什么需要在信号与系统分析中引入“复变函数”？

SS-CA-APPLE：什么是解析函数？