今天你相亲了吗?相亲号匹配问题
Posted amcomputer
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了今天你相亲了吗?相亲号匹配问题相关的知识,希望对你有一定的参考价值。
Number matching: How to match guys and girls on a blind date quickly
号码匹配:相亲的男生和女生如何快速匹配
1 背景介绍
由于信息化的发展和进步,适龄男生和女生的相亲活动逐步由线下转变为线上活动。这样不仅仅节约了大量的时间,同时也能方便适龄人寻找对象。
2 样例介绍
现在有5个男生,每个男生最多能选择3个女生,也可以选择1个或者不选。同时也有5个女生,每个女生最多能选择3个男生,也可以选择1个或者不选。选中规则,在线上相亲过程中,男女双方会有自己的号码,通过比较双方的年龄,身高,收入情况,以及其他条件做出判断,要不要选择他或者她。如果女生选中男生,而男生也选中了女生,即男女双方互相选择,则视为选中,表示相亲成功!后续相亲公司或者红娘会安排见面等流程。
对于1号男生,所选女生情况为:[2,4,5]
对于2号男生,所选女生情况为:[1,4,5]
对于3号男生,所选女生情况为:[1,3,5]
对于4号男生,所选女生情况为:[1,2,4]
对于5号男生,所选女生情况为:[2,3,4]
男生所选数组构出:[ [2,4,5],
[1,4,5],
[1,3,5],
[1,2,4],
[2,3,4]
]
对于1号女生,所选男生情况为:[1,2,5]
对于2号女生,所选男生情况为:[2,4,5]
对于3号女生,所选男生情况为:[2,4,5]
对于4号女生,所选男生情况为:[1,2,3]
对于5号女生,所选男生情况为:[1,3,4]
同理,可以得到女生所选数组:
[ [1,2,5],
[2,4,5],
[2,4,5],
[1,2,3],
[1,3,4]
]
2.1 规则介绍
对于1号男生,所选女生情况为:[2,4,5], 即选择了:2,4,5号女生
而对于2,4,5号女生所选男生情况分别为:[2,4,5],[1,2,3],[1,3,4]
即2号女生选择了:2,4,5号男生
即4号女生选择了:1,2,3号男生
即5号女生选择了:1,3,4号男生
因此,1号男生可以与4和5号女生匹配成功(因为互相选中了),进而相亲平台或者公司可以进一步帮助他们、促进发展。
3 传统思想
上一小节,样本少,所选数目也比较少。但在现实情况中,往往有几百人甚至几千人共同在相亲平台上进行选择,如果通过人工匹配的方式,讲变得尤为麻烦,需要耗费大量的人力和物力。
最初的匹配思想是先遍历每个男生,然后从中获取到所选女生号码。再从所选号码对于的女生数组中进行匹配,如果匹配得上,那么男生相亲数+1,反之为0
下面尝试用代码实现上述过程:
def matchNumber(boysList, girlList):
numBoy = len(boysList)
numgirl = len(girlList)
bildBoyScore = [0 for i in range(numBoy)]
bildGirlScore = [0 for i in range(numgirl)]
K = len(boysList[0]) # 所选人数
for i in range(numBoy):
chooseGirls = boysList[i]
for k in chooseGirls:
girlChoosed = girlList[k-1]
for j in girlChoosed:
if i+1 == j: #如果互相选中,i从0开始
bildBoyScore[i] += 1
bildGirlScore[k-1] += 1
return bildBoyScore,bildGirlScore
bildBoyScore,bildGirlScore = matchNumber(boysList, girlList)
print("男生分数:",bildBoyScore)
print("女生分数:",bildGirlScore)
输出:

用上述数据测试了一下,输出结果为上图
验证一下,对于1号男嘉宾,选了,2,4,5号女生,而4,5号女生也选了1号男嘉宾。故得分为2
再验证一下,对于5号男嘉宾,选了2,3,4号女生,2,3号选了5号男嘉宾。而4号女生选得是1,2,3号男嘉宾。故5号男嘉宾匹配上了2次。得2分。
验证1号女生,输出分数为1分。1号女生选了1,2,5号男生。而只有2号男生选了她,故得分为1。
时间复杂度分析:O(nKK),
空间复杂度分析:O(n*K)
因为男生和女生数目一样,n表示了对应个数。而K表示了可以选择的最大个数。
但是如果男生数目和女生数目不一样时,n = max(男生数目,女生数目),当n和k接近于无穷时,时间复杂度还是比较高的
4 所提方法
目标希望降低到:
时间复杂度分析:O(nK),
空间复杂度分析:O(nm)
n为男生数目,m为女生数目
通过一个网络矩阵来降低复杂度。简单一点,直接上代码了。
def matchNumberWithGrid(boysList, girlList):
numBoy = len(boysList)
numgirl = len(girlList)
matrixBoyWithGirl = []
GridScore = [[0 for i in range(numgirl)] for i in range(numBoy)]
K = len(boysList[0]) # 所选人数
for i in range(numBoy):
for j in range(K):
chooseGirls = boysList[i]
GridScore[i][chooseGirls[j]-1] += 1
for m in range(numgirl):
for j in range(K):
chooseBoys = girlList[m]
GridScore[chooseBoys[j]-1][m] += 1
return GridScore
GridScore = matchNumberWithGrid(boysList, girlList)
print("男生与女生分数分数:")
for i in GridScore:
print(i)
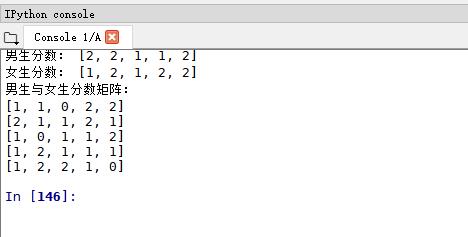
分数矩阵中的含义为:
0表示没有选择,或者没有被选择。
1表示有选择,或者被选择。
2表示有选择,并且被选择。即互相选择成功
对于输出的第一例,分数为2的有2个,即坐标为(1,4)和(1,5),表明了1号男生和4,5号女生互相选择了。和第一种输出一样。1号男嘉宾选择成功2次,得2分。
5 总结
针对目前流行的相亲号匹配问题,本文给出了具体的形式化,并且给出了传统方法的解。在此基础之上,由于复杂度过高,提出了基于网格思想的求解方案,成功的把时间复杂度降为了O(n*K), 大大的提高了效率。
 创作挑战赛
创作挑战赛
 新人创作奖励来咯,坚持创作打卡瓜分现金大奖
新人创作奖励来咯,坚持创作打卡瓜分现金大奖
以上是关于今天你相亲了吗?相亲号匹配问题的主要内容,如果未能解决你的问题,请参考以下文章