[机器学习与scikit-learn-35]：算法-分类-支持向量机-线性分类代码示例

Posted 2022-03-30 文火冰糖的硅基工坊

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/123800789

---

目录

前言：

第1步骤：导入库

第2步骤：导入数据集并可视化

 第3步骤：数据的预处理

第4步骤：建模模型并训练模型

第5步骤：可视化模型预测效果

---

前言：

本章通过代码演示支持向量机SVM实现线性分类，并调整不同的超参数，来观察对算法效果的影响。

第1步骤：导入库

import numpy as np
import matplotlib.pyplot as plt

第2步骤：导入数据集并可视化

from sklearn import datasets

iris = datasets.load_iris()

X = iris.data
y = iris.target
print("原始数据集特征数据形状", X.shape)
print("原始数据集标签数据形状", y.shape)

# 只截取标签为0和1的分类
# 且只截取第0和第1特特征值，即二维特征值
X = X[y<2, :2]
y = y[y<2]
print("截取数据集特征数据形状", X.shape)
print("截取数据集标签数据形状", y.shape)
# 只有100个样本符合要求，且样本数据从4特征降低到2个特征

#可视化数据集
# X二维矩阵=> 取值方法 x = X[行号，列号]
# X二维矩阵=> 取值方法 x = X[100， 2]
# 红色显示标签值等于0的数据
# 蓝色显示标志值等于1的数据
#                  X                 Y
### X：【标签值等于0的哪些行， 第0号特质值】
### Y：【标签值等于1的哪些行， 第1号特质值】

print(X[0])
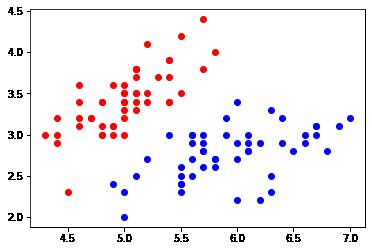
plt.scatter(X[y==0,0], X[y==0,1], color = 'red')
plt.scatter(X[y==1,0], X[y==1,1], color = 'blue')
plt.show()

原始数据集特征数据形状 (150, 4)
原始数据集标签数据形状 (150,)
截取数据集特征数据形状 (100, 2)
截取数据集标签数据形状 (100,)
[5.1 3.5]

 第3步骤：数据的预处理

# 数据预处理
from sklearn.preprocessing import StandardScaler
print("转换前=", X[0])
standardScaler = StandardScaler()
# 用数据预处理拟合样本数据，实际上是计算样本数据的参数。
standardScaler.fit(X)
# 用模型对样本数据进行格式的转换
X_standard = standardScaler.transform(X)
print("转换后=", X_standard[0])

print(X_standard[0])
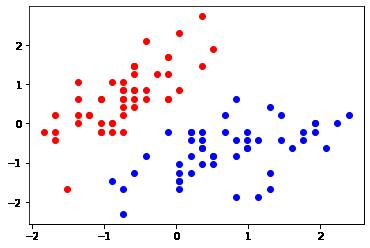
plt.scatter(X_standard[y==0,0], X_standard[y==0,1], color = 'red')
plt.scatter(X_standard[y==1,0], X_standard[y==1,1], color = 'blue')
plt.show()

#数据的分布没有变化，数据的数值范围发生了变化

转换前= [5.1 3.5]
转换后= [-0.5810659   0.84183714]
[-0.5810659   0.84183714]

第4步骤：建模模型并训练模型

# 定义线性模型
from sklearn.svm import LinearSVC

# 核心代码
# C参数影响拟合图形，可以通过调整C参数完成对模型的调控
# C越大，容错能力越弱, C越小，容错能力越弱
# C= 10: 隔离带无数据
# C= 1:  少量边界点数据
# C= 0.1：一半的数据在隔离带内
# C = 0.01：全部的数据在隔离带内

C = 0.1  # 10， 1, 0.1
svc = LinearSVC(C=C)
svc.fit(X_standard,y)

# 直线方程：w1x1 + w2x2 + b = 0
w = svc.coef_
b = svc.intercept_
print("w=",w)
print("b=",b)

# 用训练好的模型进行预测
y_predict = svc.predict([[0.2, 0.8]])
print("y_predict=", y_predict)
y_predict = svc.predict([[0.8, 0.2]])
print("y_predict=", y_predict)

w= [[ 0.89242526 -0.74178154]] 
b= [0.09160424]
y_predict= [0]
y_predict= [1]

第5步骤：可视化模型预测效果

def plot_svc_boundary(model, axis):
    # 在X轴上取100点
    x_line = np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100))
    # 在Y轴上取100点
    y_line = np.linspace(axis[0], axis[1], int((axis[3]-axis[2])*100))
    # 用x_line，y_line构建网格点向量
    x0, x1 = np.meshgrid(x_line, y_line)
    # 构建网格向量X
    X_new = np.c_[x0.ravel(), x1.ravel()]
    # 对网格平面上的所有点进行预测,输出各自的类别0或1
    
    y_predict = model.predict(X_new)
    print("y_predict.shape",y_predict.shape);
    zz = y_predict.reshape(x0.shape)
    print("zz.shape",zz.shape);
    
    # 彩色可视化
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EE9A9A', '#FFF59D','#90CAF9'])
    plt.contourf(x0, x1, zz, cmap=custom_cmap)
    
    w =  model.coef_[0]
    b =  model.intercept_[0]
    # w0 * x0 + w1 * x1 + b => x1 = -w0/w1 * x0 - b/w1
    plot_x = np.linspace(axis[0], axis[1], 200)
    up_y = -w[0]/w[1] * plot_x - b/w[1] + 1/w[1]
    dw_y = -w[0]/w[1] * plot_x - b/w[1] - 1/w[1]
    
    up_index = (up_y >=axis[2]) & (up_y <= axis[3])
    dw_index = (dw_y >=axis[2]) & (dw_y <= axis[3])
    plt.plot(plot_x[up_index], up_y[up_index], color="black")
    plt.plot(plot_x[dw_index], dw_y[dw_index], color="black")

# 根据可视化后的结果可以看出，原始数据normalization之后的数据，落在【-3，+3】之间
# 因此设置坐标值的范围如下：
xy = [-3, 3, -3, 3] 
plot_svc_boundary(svc, axis=xy)

plt.scatter(X_standard[y==0,0], X_standard[y==0,1], color = 'red')
plt.scatter(X_standard[y==1,0], X_standard[y==1,1], color = 'blue')
plt.show()

y_predict.shape (360000,)
zz.shape (600, 600)

（1）C = 10时

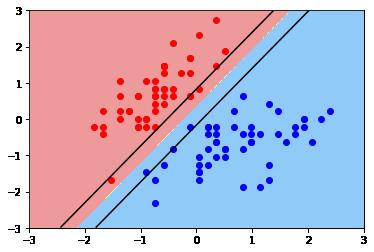
（2）C = 1时

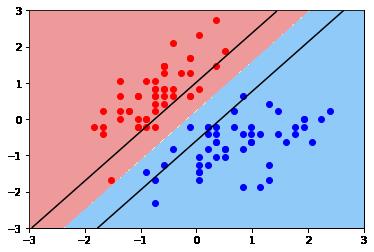
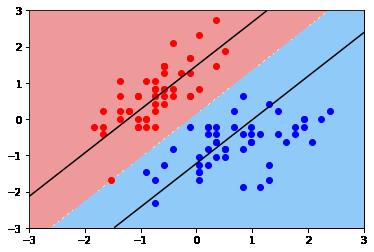
（3）C =0.1时

---

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/123800789