论文解读基于MLIR的矩阵乘法高性能GPU代码生成：一些早期结果

Posted 2022-03-28 just_sort

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了论文解读基于MLIR的矩阵乘法高性能GPU代码生成：一些早期结果相关的知识，希望对你有一定的参考价值。

0x0. 前言

本文是对 https://arxiv.org/abs/2108.13191 这篇论文进行解读，学习一下如何基于MLIR编译器基础设施生成高效的GPU代码。本文的阅读的先后顺序分别为：

标题
摘要
引言
结论
背景
设计
实验
评论

这篇论文是MLIR支持Tensor Core工作对应的论文，这篇论文涉及到的代码在llvm-project中已经开源。

0x1. 标题

本文题目为基于MLIR的矩阵乘法高性能GPU代码生成：一些早期结果。这说明论文可能还会继续完善，也许是实验或部分还要补充吧。作者团队是来自PolyMage Labs以及印度理工学院的。

0x2. 摘要

这篇文章介绍了使用MLIR编译器基础架构针对NVIDIA GPU上的Tensor Core生成代码的一些结果。当前高性能深度学习的最新技术主要由高度调优的库驱动。这些库通常由专业的程序员在low-level的级别进行手工优化和调优，并付出了很大的努力。对于类似的硬件或者将来可能出现的新硬件，可能需要重复很多这样的工作以及努力。因此，这个过程不像LLVM这样的编译器基础设施那样模块化以及可重用性很强。手工优化通常不使用IR，尽管这些优化可以被编码为一系列在IR上定义的pass。手工调优也可能会错过只有通过自动代码生成才可以轻松实现的一些优化点。本文认为，在引入MLIR之前，IR基础设施并不能有效地解决自动生成特定领域库的问题。特别是，很难使用单个IR来表示和转换高，中，低级别的抽象。

通过MLIR中的适当抽象，我们构建了一个实验性的递降(lowering)管道(pipline)，该管道可以自动生成基于GPU的Tensor core硬件的矩阵乘法的代码。在我们的实验中，初始性能结果表明，可以在NVIDIA的Ampere架构上对FP32和FP16分别达到CuBLAS性能的95-119%和80-160%的性能（显卡为Geforce 3090 RTX）。我们相信，这些结果可以作为使用IR基础设施进一步研究和开发为类似的专业加速器自动生成代码和库的动力。

0x3. 引言

深度学习和人工智能通常严重依赖于高性能计算。计算机硬件和微架构，库，编译器，运行时和编程模型的创新不断满足相关的计算需求。目前，大量高性能深度学习应用由硬件厂商提供的高度优化的库所支持，如CuDNN，CUBLAS和MKL（现在应该更名为oneDNN了）等。创建这些库需要大量的努力和专业知识，且这个开发过程可能必须在每种硬件或者软件版本中重复，并且可以有效地探索和优化的内容都是有限的。

矩阵乘法计算Kernel是许多基于Transformer（如Bert）架构的核心。它还可以作为了一个良好的测试样例来衡量可以实现的目标。虽然自动代码生成器的优势通常是优化Kernel的组合形式，而不是单个Kernel，但无法为研究充分的Kernel自动生成接近硬件峰值性能的代码难以让自动代码生成整个故事自洽。在本报告中，我们专门针对NVIDIA GPU Tensor Core，这是用于矩阵乘累加（MMA）操作的专用单元，其吞吐量通常是普通CUDA核心的3-4倍。

最近已经有一些工作聚焦于GPU Tensor Core上的 GEMM。Faingnaert 等人尝试通过在Julia创建一个三层API来解决这两种语言的问题，使得用户可以编写高效的GEMM Kernel。它们的主要关注点是开发足够灵活的API来满足各种应用程序的需求，而不是使用具有多个抽象级别的统一IR基础架构。Bhaskaracharya等人使用多面体代码生成的方法为Volta Tensor Core生成代码，它们使用调度树来表示计算并使用ISL[27]并为其生成CUDA代码。它们可以为MatMul和融合操作（如BiasAdd+ReLU）生成代码并实现高达2.55倍加速。这项工作是针对Volta的，包括一些特定于硬件的优化以实现高性能。Tillet等提出了Triton，一种IR和神经网络计算优化编译器。该框架基于tile的概念，tile是一个静态的多维数组。Triton编译器被暴露为一个Python包，它允许用户编写Python代码，编译器将自动生成高效的机器码。这项工作同时支持CUDA和Tensor Core并取得了很好的性能。

本文的方法使用编译器中间表示（IR）基础设施来做高性能代码库生成。这里使用矩阵乘法Kernel进行实验，以NVIDIA Tensor Core为目标后端。MLIR是我们在这里使用的编译器基础设施，其目标是在很大程度上使整个过程更加模块化，系统化和自动化。我们证明，通过逐级递降IR并应用正确的IR转换和优化，我们实现了和手写库相当的性能，而无需实际手动编写任何代码。虽然之前的工作对CPU单核的高性能实现进行了类似的研究，但我们这里的目标是专用的加速器。

本文贡献：

在 MLIR Dialect中引入 Warp Matrix Multiply Accumulate (WMMA) [13] Operation，并将它们递降到 LLVM/NVPTX 后端。
演示如何将 GPU 上的 matmul 系统地和渐进地生成为一系列 MLIR 变换和dialect loweing pass的代码。
构建针对Tensor Core的端到端matmul代码生成管道，初步结果表明，获得的性能与手动优化库的性能相当，在某些情况下加速达到1.60倍。

如果存在从此类模型到 MLIR 的递降(lowering)路径，我们这个基于 IR 的方法可以与不同的编程模型和语言一起使用。

本节强化了摘要，先列举了一系列和GPU Tensor Core GEMM的相关工作，这些工作有手工开发库的，也有Triton这种基于编译器的。然后作者引出本文的思路是基于MLIR这个基础设施来探索一下生成高性能的GPU Tensor Core GEMM代码，并列出了本文的贡献。（可以看出这篇论文是MLIR的一个应用，偏工程方向。

0x4. 结论

我们展示了针对NVIDIA Tensor Core支持的专用MatMul指令做自动代码生成的早期结果。这些初步结果表明，在许多情况下，自动代码生成器可以实现和手工优化库想媲美的性能。在NVIDIA Geforce 3090 PTX（基于NVIDIA Ampere架构）上的实验结果证明了本文方法的有效性。本文的研究只是设计鲁棒的代码库生成器的奠基石，它们不仅可以优化单个kernel，还可以实现kernel的组合和融合。这是一个众所周知的优化库有局限性的领域。虽然人们已经在通过DSL编译器或者图重写器来实现融合及代码生成方面付出了很多努力，但仍然缺少基于一个统一的IR基础设施的鲁棒性方法。

我总感觉这个结论怪怪的，似乎没说完。作者可能是想说，本文基于MLIR的方法让这种基于统一的IR基础设施针对特定加速器进行代码生成和优化成为了可能，并且因为接入了MLIR基础设施图重写也更加方便。

0x5. 背景

0x5.1 MLIR

MLIR的介绍这里就不多说了，我之前解读过MLIR的论文，感兴趣可以看看：MLIR：摩尔定律终结的编译器基础结构论文解读。

这个工作和MLIR的几个Dialect是有关的，这里再简要介绍一下这几种Dialect。

Affine Dialect：这种Dialect使用来自多面体编译的技术使依赖分析和循环转换高效可靠。我们已经在Affine Dialect级别进行了大部分优化和转换。
GPU Dialect：MLIR中的GPU Dialect模拟了类似于CUDA或OpenCL的通用GPU编程范式。它的目标是提供抽象来模拟 GPU 特定的操作和属性。它在很大程度上意味着与供应商无关。一些附加信息可以在 [11, 12] 和 GPU Dialect文档 [16] 中找到。
NNVM Dialect：由于我们专注于Tensor Core代码生成，我们使用和扩展 NVVM Dialect。这种Dialect提供了直接映射到 LLVM 中的 NVPTX 后端的操作。
LLVM Dialect：代码生成的最后阶段涉及递降到 LLVM IR，LLVM 后端从这里控制并生成目标代码。为了对 LLVM IR 进行建模，使用了这种Dialect。这是 MLIR 中存在的最低抽象级别。

0x5.2 GPU背景

GPU是通用的大规模并行计算设备。内存和计算层次结构在优化任何应用程序从而实现高性能方面发挥着重要作用。我们可以将GPU内存抽象为4级层次结构，global memory，L2-cache，可配置的L1-cache(shared memrory)，和寄存器。GPU上的处理器也可以抽象为两级层次结构，即流式多处理器（SM）和SM内的计算核心。计算核心通常也被叫作CUDA Cores。除了CUDA cores之外，tensor cores这种特殊单元也在较新的GPU中出现在和CUDA cores同一级别的计算层次结构中。每个SM被进一步划分为具有各自warp调度器的处理块。GPU的编程模型的结构也和当前的处理器层次结构相匹配。线程是GPU上可以和其它线程并行执行的单个执行实体。这些线程以32个为一组，叫作warp。warp在SM的计算核心上以锁步的方式执行。warp调度器选择一个准备好执行的warp并将其派发到compute cores。当一个warp碰到数据依赖时它会停止，并且warp调度器会选择另一个准备好执行的warp。

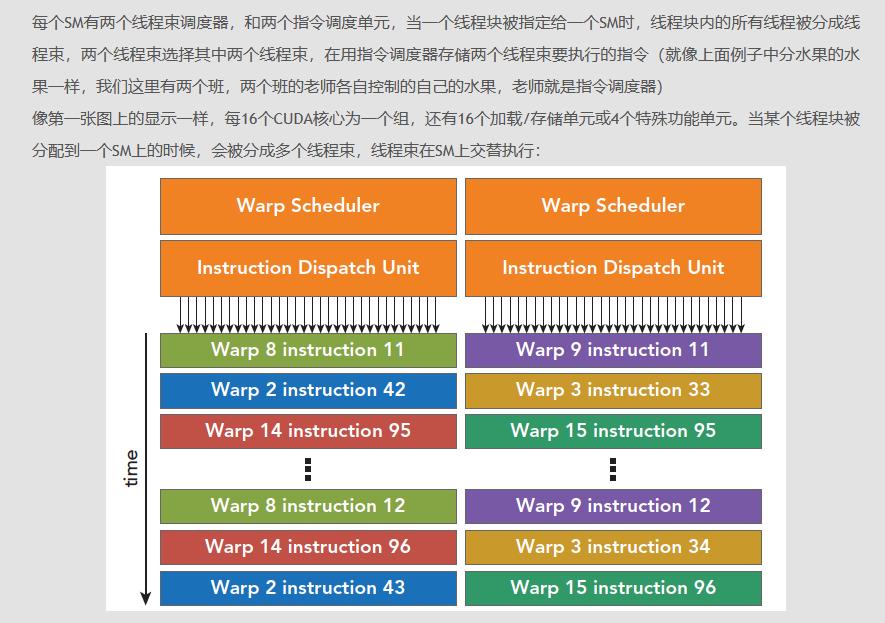
根据SM上要处理的block的数量，可能会并行执行多个warp。因此，一般而言，更多的wrap有助于实现：（i）warp级别的并行。(ii) 更好的延迟隐藏（iii）更好的利用底层资源。现在，这些 warp 被进一步分组到一个线程块中。可以有多个线程块在 GPU 上并行执行。一个线程块会绑定到一个SM。它在执行的生命周期中不能更改SM，必须在同一个SM上完成执行，并在完成时释放分配给它的所有资源。同一个warp中的线程可以使用warp级别的shuffle指令交换数据。同一个线程块中的所有线程都可以使用低延迟的shared memory进行通信，不同线程块中的线程需要使用高延迟的global memoey进行通信。同步源语存在于线程块和warp级别。根据所使用的同步类型，同步将确保线程块或warp中的任何线程都不会继续执行下一条指令，直到所有线程都到达同步点。在数据首先写入shared memory然后由所有线程读取的情况下，使用同步是必要的。在读取和写入shared memory缓冲区之前，所有线程必须同步，以确保正确性。

这段话是NVIDIA相关博客的缝合，对CUDA编程模型，执行模型以及内存模型进行了简要概述。

0x5. 3 Tensor Cores

Tensor Cores是NVIDIA GPU上的可编程矩阵乘法累加（MMA）单元。首先在Volta架构中引入，它们也出现在Turiong和Ampere架构上。显著高于CUDA cores的吞吐量使其非常适合加速深度学习的工作。它们执行表示为 $D = A * B + C$ 的MMA操作，其中操作的尺寸在Turing和Volta架构上是 $4\\times 4\\times 4$ ，而在Ampere上为 $\\times 4\\times 8$ 。Tensor cores运行像HMMA这样的warp同步指令来执行MMA操作。warp 同步意味着warp中的所有线程协同执行这些特殊指令，以产生 MMA 操作的输出。由于Tensor cores指令的这种warp同步特性，在对Tensor cores进行编程时，有必要在warp而不是线程级别编写或生成代码。 Tensor cores最初只支持FP16的输入和FP16或FP32的累加的输出。但现在它们支持多种输入和输出格式，如TF32，BF16，INT8和INT4。TF32的范围和FP32相同，精度和FP16相同，但以19位数表示。它可以用于精度允许一些损失的地方。要使用这种模式，输入必须在FP32中，它们将在内部转换为TF32，在TF32中进行累加，并且输出也在TF32中产生。这相比于Cuda cores上正常的FP32模式提供了加速。BF16提供和FP32相同的范围，但精度低于FP16。Tensor cores在BF16和FP16模式下提供相同的速度，而两者都比TF32更快。整数类型旨在用于训练后量化 [21]。

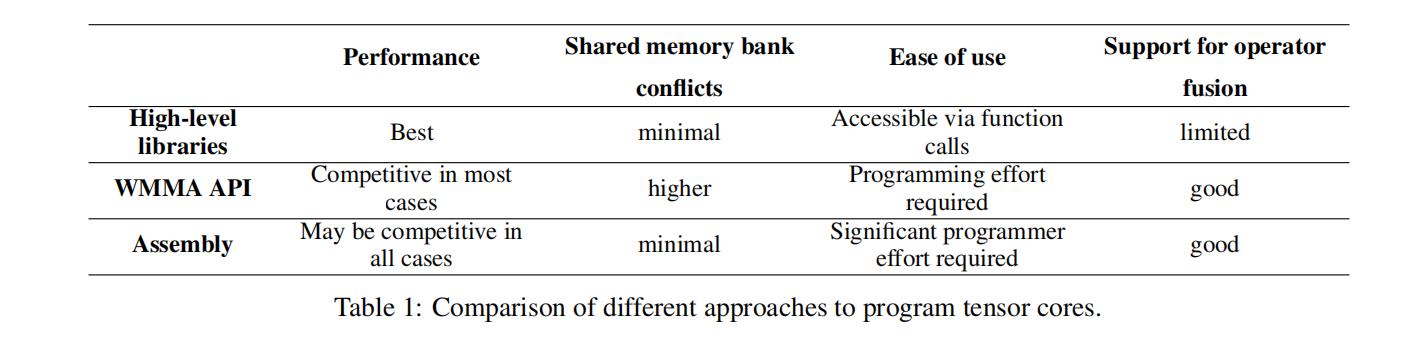
在可编程性方面，可以通过三种方式利用Tensor cores：(i) 使用像 cuBLAS 这样的高级库，(ii) 在 CUDA 中使用高级 C++ API 如WMMA[1] 进行编程，或者，(iii) 使用汇编级指令对它们进行显式编程。

使用cuBLAS只需要调用一下接口，而使用其它两种方式需要大量的编程工作。WMMA API提供大矩阵操作（ $16\\times 16\\times 16$ ， $\\times 8\\times 16$ ），以及用于加载和存储操作矩阵的实用函数。将这些API函数转换为GPU微架构特定的汇编指令的任务也被下派到NVIDIA的专用编译器中。使用 WMMA API 加载的矩阵在加载到寄存器后具有不透明的布局，即不知道哪个线程持有加载矩阵的哪个元素（线程数据映射）。由于这种不透明的性质，在与bias_add等操作进行融合时需要一些额外的步骤，这些操作需要了解线程数据映射。使用汇编指令显式编程Tensor cores甚至更具挑战性，因为程序员必须处理如寄存器中的线程数据映射以及共享内存和寄存器之间的数据移动这种复杂性。上面的Table 1总结了这些方法。

LLVM中的NVPTX后端将WMMA API函数公开为instrinsics。这使得通过MLIR对Tensor cores进行编程成为可能。这些instrinsics与 WMMA API 函数一一对应，并在编程和使用方面表现出相同的行为。

0x6. 设计

在本节中，我们将介绍管道（pipeline）的设计。我们的管道基于一系列优化和转换，这些优化和转换构成了 GPU上高性能matmul 的配方。我们使用的方法与之前的一些工作中强调的非常接近。这些方法中共同的部分是两级blocking，以最大化内存层次结构不同级别的重用。通用的方法在算法1中被描述：

在我们工作之前，MLIR 中提供了一些支持，我们在管道中重用了这些支持，但还缺少一些核心组件。主要是MLIR 中没有使用 WMMA API 对Tensor cores进行编程所需的操作，而我们是引入这些操作的人。我们会在必要时对现有的 MLIR 基础设施进行更改和添加。

Figure 1显示了我们采用的递降路径，它基于Algorithm 1。虽然可以有不同的递降路径来实现相同的目标，但我们认为应该选择通过Affine Dialect的递降路径，因为生成的目标Kernel是仿射的。这可以在许多方面有所帮助，例如快速内存缓冲区的创建和放置、loop-tiling、unroll-jam、矢量化、并行循环的检测以及同步barriers的放置等。

虽然为了简洁而没有在算法 1 中突出显示，但值得注意的是，只有使用一组更多的优化才能实现高性能，其中包括 (i) 在shared memory缓冲区中pad以减少bank conflicts，(ii) 寄存器tiling或warp tiling，（iii）load-store矢量化，以及（iv）global memory加载延迟隐藏。现在，我们将详细描述我们的递降管道，讨论如何启用主要优化。

0x6.1 起点

本文代码生成流程的起点是像lmho.dot或者linnalg.matmul这样high level的操作，或者是从面向用户的编程模型生成的linalg dialect IR中的linalg.matmul。在前一种情况下，我们可以将操作递降为一个三重循环的affine matmul，而在后者中我们可以直接生成三重循环的affine matmul。起点如List 1所示：

0x6.2 局部性和并行性的tiling

众所周知，如果为tiling选择了合适的参数是有助于数据重用并显著提升性能的。两级tiling对于GPU实现最佳性能至关重要。第一级的tiling映射到不同的线程块，每个线程块将矩阵A和B中的tile块从global memoey复制到shared memory，从而防止多次访问高延迟的global memory。由于划分的tile被映射到不同的线程块，它们可以在不同的SM上并行计算。第二级的tiling促进寄存器的重用并有助于warp级的并行。线程块级别的tile在warp之间进行划分，每个warp只在映射到它的tile的部分上起作用。这个步骤为我们提供了2个级别的tiling结构。我们从List2可以看到这两级Tiling的具体结构：

Loop Tiling，是优化循环的一种非常重要的策略。而在深度学习中，计算密集型算子如矩阵乘法，本质上就是由三层循环构成的，因此Loop tiling在这篇论文的优化中发挥了非常关键的作用。简单而言，Loop Tiling就是通过分块来减少Cache Miss，降低因为数据evict导致的性能下降。如果想了解更多可以看看 https://zhuanlan.zhihu.com/p/477023757 这篇文章或者TVM中对Loop Tiling介绍。

0x6.3 创建和放置Shared Memory缓冲区

tiling完成之后，下一步是创建shared memory缓冲区并将其放在正确的循环深度。我们使用affineDataCopyGenerate实用程序（由Affine Dialect的Transform部分提供）来生成矩阵A和B的副本。我们在这里采取的方法和以前的一些工作略有不同。我们仅为矩阵A和B创建shared memory缓冲区。由于每个warp只加载一次C，因此我们将其直接从global memory流到shared memory，然后从shared memory到寄存器。通过shared memory流式传输C的基本原理是防止对global memory的随机访问，并可能促进global memory中的合并访问，这可能更有效。但我们猜测可能并非总是如此，特别是对于大规模的问题，因为每个warp只加载一次C的tile。

关于CUDA如何更有效的访问全局内存，可以看下NVIDIA的博客：How to Access Global Memory Efficiently in CUDA C/C++ Kernels 。oneflow的zzk也把这个博客翻译成了中文版，对应地址：https://zhuanlan.zhihu.com/p/473133201 。

此外，这种方法还需要使用动态分配的shared memory，因为C矩阵的最佳tile大小很容易耗尽某些设备上的48KB静态shared memory限制。所以保存tile的缓冲区必须动态分配，并且必须被重用以存储三个操作数的小块（矩阵的A,B,C）。 MLIR 目前不支持动态分配shared memory。因此，我们将自己限制为静态分配的shared memory，以避免代码生成器中的额外复杂性，因为这可能不值得付出努力。即使不动态分配shared memory，在大多数情况下我们的性能已经接近手动调优的库。

创建shared memory是其中的一部分，而确保shared memory访问具有最小的bank conflict是另一回事。bank conflict会显著降低内存的吞吐。避免bank conflict的一般技术是pad shared memory缓冲区。我们通过将affineDataCopyGenerate生成shared memory缓冲区的leadingDimension改成leadingDimension+paddingFactor来达到同样的效果。这样做会改变shared memory缓冲区的底层布局，以考虑leading维度的变换，而IR其余部分不需要改变。还值得注意的是，我们可以在这里尝试不同的padding因子看看哪个效果最好，但是padding因此必须是8的倍数，如FP16元素取128-bit。这是因为WMMA API有内存对齐要求。

0x6.4 生成 WMMA 操作等

现在我们已经拥有了我们需要的所有基本东西，我们可以继续生成 gpu.subgroup_mmaop。 WMMA 操作有不同的大小，我们在这项工作中使用 $16 \times 16 \times 16$ 版本的操作。我们这里生成的操作应该替换掉已经存在的标量操作，相应循环的循环步数也要相应调整。

现在我们已经生成了 WMMA 操作，我们进行以下 IR 转换：

将最外面的六个循环从 $(i, j, k, i i, j j, k k)$ 顺序重排到 $(i, j, i i, j j, k, k k)$ 顺序。这稍后将有助于将计算循环映射到GPU计算层次结构。此外，它还有助于将C上不变的load-store 操作尽可能移动到最外层。
将最里面的三个循环 $(i, j, k)$ 置换为 $(k, i, j)$ 。正如 Bhaskaracharya 等人所指出的，这将warp级 MMA 操作作为外部product表示并增强了指令的并行策略。[4]。
完全unroll最里面的三个循环。

这里可能有一些理解的误区，我这里说一下我的理解，和大家交流一下。首先 $(i, j, k, i i, j j, k k)$ 经过第一个步骤变成 $(i, j, i i, j j, k, k k)$ ，然后最里面的三个循环 $(k k, k, j j)$ 从0,1,2的顺序变成2,0,1的顺序也就是 $(j j, k k, k)$ ，然后现在整个循环的顺序为 $(i, j, i i, j j, k k, k)$ ，再经过unroll之后kk被展开。那么最终的循环排列顺序为 $(i, j, i i, j j, k)$ ，和Listing 3的顺序是一致的。

上面的Listing 2显示了我们在创建了WMMA操作后获得的IR。我们应该注意这里调整最内存循环的步骤。这个清单进一步显示了循环嵌套中我们想要的的排列。最外面的两个循环稍后将映射到grid中的线程块，随后的两个循环将映射到warps。接下来的两个循环是对应于线程块的k-loops，然后是warp。unrool之后，我们观察到：（1）C 矩阵上的操作现在变得独立于两个紧邻的循环，因此我们现在将C上的操作提到最外面的k循环。通过这种方式，我们可以防止在global memory中对 C 进行重复加载和存储，并且仅在线程块tile的处理开始和结束时执行它们。（2）展开这些循环揭示了A和B上的所有loads。这些loads在k维上是相同的，通过应用CSE，我们完全可以去除多余的load，实现unroll-jam的效果。

关于unroll-jam可以看一下陈清杨大佬的这篇文章：https://zhuanlan.zhihu.com/p/392892255

上述优化后的循环结构如Listing 3所示。需要注意循环结构在C矩阵的不变load-store对移动后发生了什么样的变化。第20行的affie.for操作代表main k循环，现在修改为将load的C操作数作为循环iter_args、这些将用作此循环中发生的乘法的累加器。每次迭代后，这个k循环都会产生累加的结果，并将这些结果作为iter_args传给下一次迭代。这些iter_args驻留在寄存器中，并在k循环的不同迭代中重复使用。

0x6.5 Global Memory加载延迟隐藏

随着上一节中 gpu.subgroup_mma op 和其他一些优化的引入，我们正在朝着最终 IR 中的结构迈进。我们专注于本身没有任何GPU特定信息的Affine Dialect中做尽可能多的优化。在我们目前的 IR 中，在加载A和B的shared memory之前，我们无法开始计算。就延迟而言，global memory load是最昂贵的操作之一，因此消除操作数的长等待时间非常重要的。我们通过拆分main k-loop或线程块k-loop在第0个迭代中取出A和B的副本并为n-1个迭代通过计算来做到这一点。副本放在 k-loop之前，计算紧随其后。每次迭代时在该循环中执行的计算的索引也需要向前移动移动一次。结果是，计算发生在shared memory中已经可用的数据上，并且已经发出了下一次迭代的load(这个其实就类似PyTorch DataLoader类似的prefetch)。我们在此展示 IR 的结构清单 4 中的IR。

虽然这为延迟隐藏奠定了基础，但要实现这一点，我们需要将存储到shared memory与加载到global memory解耦，方便线程块 k-loop内的copy循环。这对于优化的正确性和功能都是必需的。为此，我们unroll copy loop并在k-loop外部将store延迟到尾部。我们将这种优化延迟到管道中的另一点，因为启用它需要一些特定的GPU信息。

0x6.6 插入同步barrires

我们已经完成了IR中大部分的生成，这可能需要同步barrires。 shared memory缓冲区将被线程块中的所有线程读写，因此必须在写入这些缓冲区之前和之后进行同步。一般来说，这个过程也可以使用基于内存的依赖分析来自动化。然而，为了我们当前的目的，我们使用上述关于copy循环的静态信息来放置这些同步barrires。

0x6.7 Global到Shared Copy矢量化

虽然延迟隐藏会发挥作用，但它不能使实际的copy运行得更快。众所周知，向量加载存储指令 [17] 比它们的标量指令执行得更好，因为它减少了内存访问的数量，并且通常可以更好地利用可用带宽。

我们使用 MLIRX [24] 中已经存在的向量化实用程序。我们将此实用程序称为global到shared memory的copy。我们可以使用此实用程序尝试不同的向量宽度。我们尝试了32、64和128位宽的向量，发现128位宽的向量效果最好。矢量化copy循环如Listing 5所示：

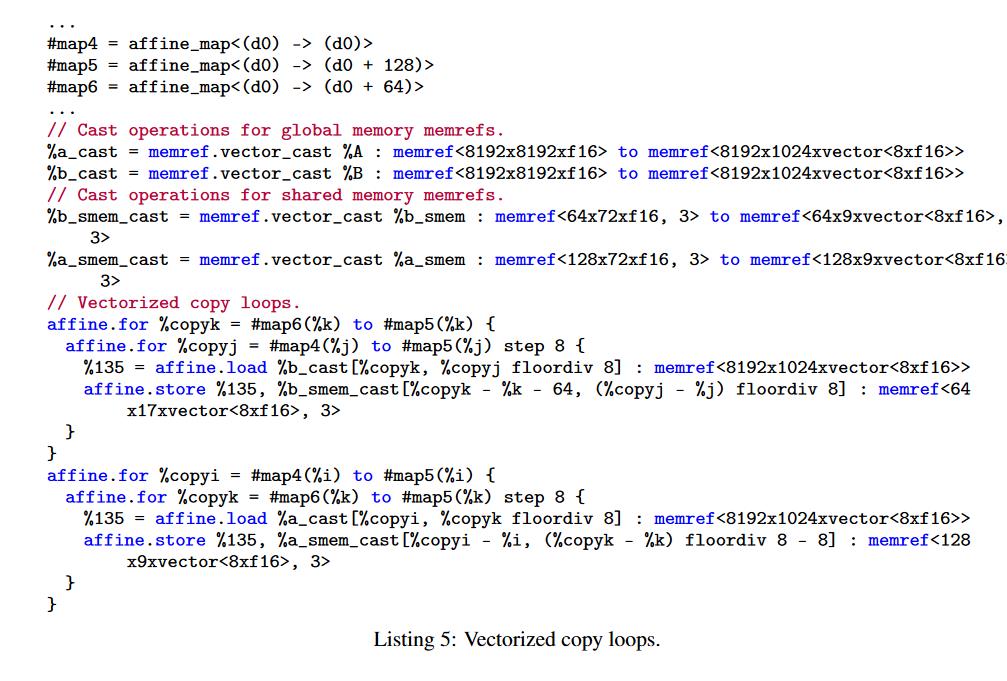
可以对比Listing 4，这里有一个vector_cast的向量化操作。

0x6.8 提取并行循环

这是我们在Affine Dialect中采取的最后一步。我们使用 MLIR 中的 isLoopParallel 实用程序来查找所有可以并行循环，然后使用 affineParallelize 将它们并行化。这些并行循环稍后会被处理并映射到GPU处理器层次结构，而顺序循环是唯一保留在kernel中的循环。

0x6.9 映射到 GPU 计算层次结构

上一步是Affine Dialect中的最后一步，之后我们立即将IR转换为SCF Dialect。SCF Dialect开始后做的第一件事就是将并行循环映射到GPU计算层次结构。MLIR中用于映射的现有实用程序和pass不支持将循环映射到单个warp，这在我们的案例中是必需的。我们扩展了实用程序和pass以添加对 matmul 的支持。理想情况下，我们应该通用化此步骤中使用的pass和实用程序来处理各种循环嵌套，我们将其留作未来的工作。在这一点上值得指出的是，我们采取了所有必要的措施来确保coalesced global memory访问 [10]，这对于有效利用带宽和更快地从global memory复制到shared memory至关重要。映射完成后，最外面的两个循环将转换为 gpu.launch op，接下来的两个循环将映射到warp，其余的计算循环（指的是k-loop）实际上是顺序的并保持原样。

coalesced global memory可以看NVIDIA的这篇博客：https://developer.nvidia.com/blog/how-access-global-memory-efficiently-cuda-c-kernels/

0x6.10 完成延迟隐藏

在0x6.5节我们描述了延迟隐藏并得出结论，但需要等到我们将load和store解耦它才可以完成。为了在不引入任何代码复杂性的情况下实现这一点，我们首先在线程块k-loop内完全展开(unroll) copy循环，然后延迟store以便它们在计算完成后发生。我们在Listing 6中展示了IR的一般结构，我们遵循的方法和[4]中提到的很类似。

这是我们优化的终点，也是我们在 SCF Dialect中的最后一步。

0x6.11 放到一起

由于上一步是优化方面的最后一步，因此现在要设置生成的IR以提供执行。 MLIR 中已经存在设计良好的基础设施来实现这一点 [12 , 11 ]，为了完整性，我们提供了一个概要大纲。 MLIR 中的现有设计允许在单个 MLIR 文件中表示在 GPU 等加速器上执行的IR。IR将包含两部分：运行在 CPU上的host端组件和运行在GPU上的device端组件或kernel。host端组件调用device端组件，并且可以等待其执行完成或者可以继续执行其他任务。host端和device端组件的递降路径略有不同：

Host端编译：host端的代码被转换为std dialect然后转换为llvm dialect。在转换为llvm dialect期间，来自GPU dialect的操作如gpu.launch通过MLIR CUDA运行时API函数调用将其递降为LLVM IR，并生成目标代码。然后通过mlir-cpu-runner执行IR（MLIR提供的jit）。它将要链接的共享库作为参数，我们可以在其中提供与CUDA驱动程序API对应的库。
Device端编译：device端代码也被转换为std dialect，然后转换为llvm和nnvm dialect的混合。这又被转换为LLVM IR，然后由LLVM的NVPTX后端转换为PTX。然后使用NVIDIA的编译器将PTX转换为cubin（CUDA二进制格式）。NVIDIA的编译器通过MLIR的CUDA驱动程序API调用。MLIR中的gpu-to-cubin pass可以访问驱动程序API，并为我们执行PTX到cubin的编译和嵌入。我们扩展了此pass以使用一些其它选项，例如优化级别和每个线程的最大寄存器数，这是将PTX编译到cubin时需要的。

执行这些最终步骤的基础设施已经存在于 MLIR 中。虽然我们的评估使用了 MLIR JIT，但也可以使用类似的设置执行提前编译。我们引入的 GPU dialect操作 gpu.subgroup_mma_load_matrix、gpu.subgroup_mma_store_matrix 和 gpu.subgroup_mma_compute 已开源并上传到官方 LLVM/MLIR 存储库。

0x7. 评估

在本节中，我们将展示我们的Kernel的性能并将它们与 CuBLAS 11.2 进行比较。评估是在基于 NVIDIA Ampere 的 Geforce RTX 3090 上执行的，该 Geforce RTX 3090 安装在 x86-64 系统上，配备 AMD Ryzen Threadripper 3970X CPU，运行 Ubuntu 20.04 LTS系统。为所有实验设置了以下参数：

所有实验的SM 适中评论设置为白皮书中提到的最高频率，即 1695 MHz。
我们将自己限制为静态分配的shared memory，即 48 KB。
每个线程的最大寄存器数设置为 255。

我们使用 NVIDIA Nsight Systems [23] 进行计时，并且仅考虑kernel运行时来计算达到的 TFLOPs。这适用于我们的kernel以及 CuBLAS。我们考虑线程块级别的tile和warp级别tile的不同组合，并报告性能最佳的版本。报告的性能已平均超过十次运行。

最后，我们考虑 $C = A B + C$ 形式的 matmul（所有三个矩阵都存储在行优先布局中）。我们使用WMMA指令 $16\\times 16\\times 16$ 的版本并将问题规模限制为从1024到16384的平方大小，步长为256。我们假设问题规模大小是线程块tile的倍数，也是warp tile的倍数。

0x7.1 混合精度的表现

在本节中，我们将展示我们自动生成的混合精度kernel的性能。在 F16 中具有 A、B 的矩阵-矩阵乘法以及在F32中进行的乘积的累加称为混合精度 matmul。输出矩阵C，也在 F32中。我们对这个版本特别感兴趣，因为它在训练深度学习模型中很重要 [22]。

我们实现的性能始终在CuBLAS 11.2 的 95-119%范围内。将我们的性能与设备的绝对峰值进行比较，我们维持了设备峰值的 95.4%。Figure 2显示了我们自动生成的kernel在 Ampere RTX 3090上的性能。该图显示我们的结果非常接近 cuBLAS。在一些较小的尺寸上，我们的表现优于cuBLAS。一般来说，cuBLAS kernel对于较小尺寸的调整可能不如对较大尺寸的性能好。在较大尺寸上，MLIR 生成的代码性能在cuBLAS性能的2-8%范围内。进一步观察到，较小的线程块大小（如 $64\\times 64\\times 64$ ）在较小的问题大小上表现更好。这表明较小的问题规模受益于增加的occupancy。这表明较小的问题规模受益于增加的占用率（占用率是指每个多处理器（Streaming Multiprocessor，SM）的活动线程束（warps）数量与实际的活动warps数量的比率。高的占用率不一定能提升性能，但低的占用率会降低内存延迟隐藏的作用）。虽然较小的 tile 大小会减少共享内存中 A 和 B 的重用，但它们会增加占用率，这有利于较小的问题大小，可能会启动相对较少的线程块。在大size上，tile尺寸太小会导致相对较多的小线程块，减少数据重用的效果更加突出，占用率不再有明显收益。

自动代码生成方法还允许我们通过有选择地启用或禁用优化来研究单个优化的影响。我们以增量方式在Figure 3中展示了前面讨论的每个优化的影响，从原始版本到完全优化的版本。

0x7.2 半精度的表现

在本节中，我们展示了自动生成的半精度kernel的性能。在这个版本的 matmul 中，所有三个矩阵 A、B 和 C 都在 FP16 中。结果的累加也是在FP16完成的。此版本通常比 F32 版本快，但由于尾数和指数的表示较窄，可能容易出现精度不够的问题。

我们实现的性能始终是 cuBLAS 11.2 的 80-160%。 Figure 4 显示了我们自动生成的kernel在 Ampere RTX 3090 上的性能。我们观察到cuBLAS在整个范围内的性能都不一致，特别是在大于 W = 8848 尺寸的问题上。这表明 cuBLAS 并未针对所有问题大小进行良好调整。特别是，在分析 cuBLAS kernel时，我们观察到 cuBLAS 选择的线程块大小实际上小于我们具有最佳性能的大小，例如，对于 W=11264，cuBLAS 选择 $128\\times 128\\times 32$

MLIR：摩尔定律终结的编译器基础结构论文解读