本科课程数据结构与算法实验6 - 创建哈希表最短路径(Dijkstra算法)
Posted 1 + 1=王
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了本科课程数据结构与算法实验6 - 创建哈希表最短路径(Dijkstra算法)相关的知识,希望对你有一定的参考价值。
大家好,我是【1+1=王】, 热爱java的计算机(人工智能)渣硕研究生在读。
如果你也对java、人工智能等技术感兴趣,欢迎关注,抱团交流进大厂!!!
Good better best, never let it rest, until good is better, and better best.近期会把自己本科阶段的一些课程设计、实验报告等分享出来,供大家参考,希望对大家有帮助。
博客更新至专栏【课程设计实验报告】:https://blog.csdn.net/weixin_43598687/category_11640051.html
一、 实验目的
- 实现哈希表的创建
- 利用线性探测在散列处理冲突
- 掌握图的邻接矩阵表示
- 实现图的最短路径查找操作(Di jkstra算法)
二、 实验内容
1. 实验任务
(1)创建哈希表
(2)利用Di jkstra算法寻找图的最短路径
2. 程序设计
1) 数据输入(输入哪些数据、个数、类型、来源、输入方式)
输入哈希表的关键数key(int 整型)
图的顶点数据(data)char字符型;
图的边关系(v1,v2)int 整型;
各边的权值(w)int 整型
2) 数据存储(输入数据在内存中的存储)
定义结构体Hash(key,si)
以数组HashList[i]存储各条数据
采用邻接矩阵存储图
3) 数据处理(说明处理步骤。若不是非常简单,需要绘制流程图)
(1)
①哈希表的查找
储存数据时,将数据存入通过哈希函数所得的地址里,使用同一个哈希函数通过关键字key计算出储存地址,通过该地址访问到查找的记录
②冲突解决
使用线性探测再散列法(冲突发生时,顺序查看表中下一单元,直到找出一个空单元或查遍全表)
(2)
在所有从源点出发的弧中选取一条权值最小的弧,即为第一条最短路径;
设置一个顶点集合S,存放最短路径的终点。顶点k为当前最短路径的终点,将Vk加入集合S中,而Dist[k]为最短路径的长度;
每次从集合V-S中取出具有最短特殊路径长度的顶点u,将u加到S中,同时对数组Dist做必要的修改,若Dist[u]+G.arcs[u][k]<Dist[k]则将Dist[k]改为Dist[u]+arcs[u][k]。其中,特殊路径指从源点到u中间只经过S中顶点的路径;
重复操作2)、3)共n-1次1
4) 数据输出
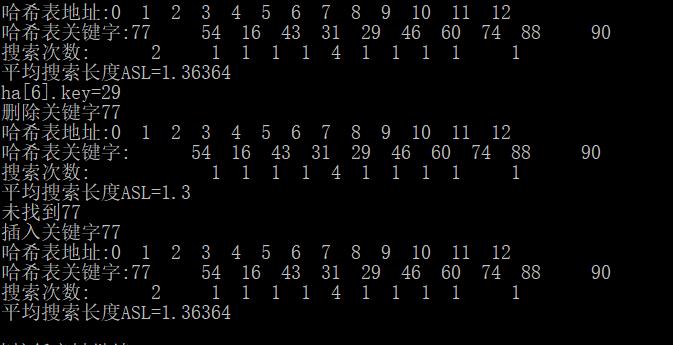

三、 实验环境
- 操作系统:WINDOWS 10
- 开发工具:VC++ 2013
- 实验设备:PC
源代码(C++实现)
创建哈希表
#include <stdio.h>
#include<iostream>
using namespace std;
#define MaxSize 100 //定义最大哈希表长度
#define NULLKEY -1 //定义空关键字值
#define DELKEY -2 //定义被删关键字值
typedef int KeyType; //关键字类型
typedef char *InfoType; //其他数据类型
typedef struct
KeyType key; //关键字域
InfoType data; //其他数据域
int count; //探查次数域
HashTable[MaxSize]; //哈希表类型
void InsertHT(HashTable ha, int &n, KeyType k, int p);
void CreateHT(HashTable ha, KeyType x[], int n, int m, int p);
int SearchHT(HashTable ha, int p, KeyType k);
int DeleteHT(HashTable ha, int p, int k, int &n);
void DispHT(HashTable ha, int n, int m);
void CompASL(HashTable ha, int m);
void main()
int x[] = 16, 74, 60, 43, 54, 90, 46, 31, 29, 88, 77 ;
int n = 11, m = 13, p = 13, i, k = 29;
HashTable ha;
CreateHT(ha, x, n, m, p);
cout << endl;
DispHT(ha, n, m);
i = SearchHT(ha, p, k);
if (i != -1)
printf(" ha[%d].key=%d\\n", i, k);
else
cout << "未找到" << k << endl;
k = 77;
printf(" 删除关键字%d\\n", k);
DeleteHT(ha, p, k, n);
DispHT(ha, n, m);
i = SearchHT(ha, p, k);
if (i != -1)
printf(" ha[%d].key=%d\\n", i, k);
else
printf(" 未找到%d\\n", k);
printf(" 插入关键字%d\\n", k);
InsertHT(ha, n, k, p);
DispHT(ha, n, m);
cout << endl;
system("pause");
//将关键字k插入到哈希表中
void InsertHT(HashTable ha, int &n, KeyType k, int p)
int i, adr;
adr = k%p;
if (ha[adr].key == NULLKEY || ha[adr].key == DELKEY)
ha[adr].key = k;
ha[adr].count = 1;
else //发生冲突时,采用线性探查法解决冲突
i = 1;
do
adr = (adr + 1) % p;
i++;
while (ha[adr].key != NULLKEY && ha[adr].key != DELKEY);
ha[adr].key = k;
ha[adr].count = i;
n++;
//创建哈希表
void CreateHT(HashTable ha, KeyType x[], int n, int m, int p)
int i, n1 = 0;
for (i = 0; i<m; i++) //哈希表置初值
ha[i].key = NULLKEY;
ha[i].count = 0;
for (i = 0; i<n; i++)
InsertHT(ha, n1, x[i], p);
//在哈希表中查找关键字k
int SearchHT(HashTable ha, int p, KeyType k)
int i = 0, adr;
adr = k%p;
while (ha[adr].key != NULLKEY && ha[adr].key != k)
i++; //采用线性探查法找下一个地址
adr = (adr + 1) % p;
if (ha[adr].key == k) //查找成功
return adr;
else //查找失败
return -1;
//删除哈希表中关键字k
int DeleteHT(HashTable ha, int p, int k, int &n)
int adr;
adr = SearchHT(ha, p, k);
if (adr != -1) //在哈希表中找到关键字
ha[adr].key = DELKEY;
n--; //哈希表长度减1
return 1;
else //在哈希表中未找到该关键字
return 0;
//输出哈希表
void DispHT(HashTable ha, int n, int m)
float avg = 0;
int i;
cout<<" 哈希表地址:";
for (i = 0; i<m; i++)
cout<<i<<" ";
cout << endl;
cout<<" 哈希表关键字:";
for (i = 0; i<m; i++)
if (ha[i].key == NULLKEY || ha[i].key == DELKEY)
cout<<" ";
else
cout<<ha[i].key<<" ";
cout<<endl;
cout<<" 搜索次数:\\t";
for (i = 0; i<m; i++)
if (ha[i].key == NULLKEY || ha[i].key == DELKEY)
cout<<" ";
else
cout<<ha[i].count<<" ";
cout << endl;
for (i = 0; i<m; i++)
if (ha[i].key != NULLKEY && ha[i].key != DELKEY)
avg = avg + ha[i].count;
avg = avg / n;
cout << " 平均搜索长度ASL=" << avg << endl;
//查找成功时,平均查找长度
void CompASL(HashTable ha, int m)
int i;
int s = 0, n = 0;
for (i = 0; i<m; i++)
if (ha[i].key != DELKEY && ha[i].key != NULLKEY)
s = s + ha[i].count;
n++;
printf(" 查找成功的ASL=%.3g\\n", s*1.0 / n);
最短路径
#include <stdio.h>
#include <stdlib.h>
#include<iostream>
#include <string.h>
using namespace std;
#define MAX 100 // 矩阵最大容量
#define INF 65535 // 最大值65535
#define LENGTH(a) (sizeof(a)/sizeof(a[0]))
// 图的邻接矩阵存储
typedef struct _graph
char vexs[MAX]; // 顶点集合
int vexnum; // 顶点数
int edgnum; // 边数
int matrix[MAX][MAX]; // 邻接矩阵
Graph, *PGraph;
// 边的结构体
typedef struct _EdgeData
char start; // 边的起点
char end; // 边的终点
int weight; // 边的权重
EData;
Graph* create_graph();
void print_graph(Graph G);
void dijkstra(Graph G, int vs, int prev[], int dist[]);
int main()
int vs;
int prev[MAX] = 0 ;
int dist[MAX] = 0 ;
Graph* pG;
pG = create_graph();
print_graph(*pG); // 打印图
cout << "从第几个节点开始寻找最短路径:";
cin >> vs;
dijkstra(*pG, vs, prev, dist);
system("pause");
return 0;
/*
* 创建图(用已提供的矩阵)
*/
Graph* create_graph()
char vexs[] = 'A', 'B', 'C', 'D', 'E', 'F', 'G' ;
int matrix[][9] =
/*A*//*B*//*C*//*D*//*E*//*F*//*G*/
/*A*/ 0, 12, INF, INF, INF, 16, 14 ,
/*B*/ 12, 0, 10, INF, INF, 7, INF ,
/*C*/ INF, 10, 0, 3, 5, 6, INF ,
/*D*/ INF, INF, 3, 0, 4, INF, INF ,
/*E*/ INF, INF, 5, 4, 0, 2, 8 ,
/*F*/ 16, 7, 6, INF, 2, 0, 9 ,
/*G*/ 14, INF, INF, INF, 8, 9, 0 ;
int vlen = LENGTH(vexs);
int i, j;
Graph* pG;
pG = (Graph*)malloc(sizeof(Graph));
pG->vexnum = vlen;
for (i = 0; i < pG->vexnum; i++)
pG->vexs[i] = vexs[i];
for (i = 0; i < pG->vexnum; i++)
for (j = 0; j < pG->vexnum; j++)
pG->matrix[i][j] = matrix[i][j];
for (i = 0; i < pG->vexnum; i++)
for (j = 0; j < pG->vexnum; j++)
if (i != j && pG->matrix[i][j] != INF)
pG->edgnum++;
pG->edgnum /= 2;
return pG;
/*
* 打印矩阵队列图
*/
void print_graph(Graph G)
int i, j;
cout << "Martix Graph:" << endl;;
for (i = 0; i < G.vexnum; i++)
for (j = 0; j < G.vexnum; j++)
printf("%10d ", G.matrix[i][j]);
cout << endl;
/*
* Dijkstra最短路径。
* 统计图(G)中"顶点vs"到其它各个顶点的最短路径。
*
* 参数说明:
* G -- 图
* vs -- 起始顶点(start vertex)。计算"顶点vs"到其它顶点的最短路径。
* prev -- 前驱顶点数组。
* dist -- 长度数组。
*/
void dijkstra(Graph G, int vs, int prev[], int dist[])
int i, j, k;
int min;
int tmp;
int flag[MAX]; // flag[i]=1表示"顶点vs"到"顶点i"的最短路径已成功获取。
// 初始化
for (i = 0; i < G.vexnum; i++)
flag[i] = 0; // 顶点i的最短路径还没获取到。
prev[i] = 0; // 顶点i的前驱顶点为0。
dist[i] = G.matrix[vs][i];// 顶点i的最短路径为"顶点vs"到"顶点i"的权。
// 对"顶点vs"自身进行初始化
flag[vs] = 1;
dist[vs] = 0;
// 遍历G.vexnum-1次;每次找出一个顶点的最短路径。
for (i = 1; i < G.vexnum; i++)
// 寻找当前最小的路径;
min = INF;
for (j = 0; j < G.vexnum; j++)
if (flag[j] == 0 && dist[j]<min)
min = dist[j];
k = j;
// 标记"顶点k"为已经获取到最短路径
flag[k] = 1;
// 修正当前最短路径和前驱顶点
// 即,当已经"顶点k的最短路径"之后,更新"未获取最短路径的顶点的最短路径和前驱顶点"。
for (j = 0; j < G.vexnum; j++)
tmp = (G.matrix[k][j] == INF ? INF : (min + G.matrix[k][j])); // 防止溢出
if (flag[j] == 0 && (tmp < dist[j])<以上是关于本科课程数据结构与算法实验6 - 创建哈希表最短路径(Dijkstra算法)的主要内容,如果未能解决你的问题,请参考以下文章