[硫化铂]启程的日子

Posted 2022-03-26 StaroForgin

启程的日子

题目概述

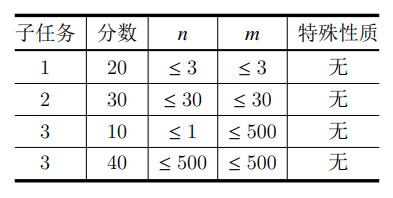
题解

我们可以先将矩阵的$+/-$看成对矩阵染色。
首先这道题不要先想到每次都将一个同色连通块全部染完的方案上面去，我们可以发现每次只染色某个连通块的一部分往往可以得到一个更优秀的答案。
我考试时那样想就…

我们先考虑一种特殊情况，许多黑白环的嵌套该怎么做。

我们如果按连通块染色的话相当于就是这个环连通块数量的直径，但事实上我们可以构造出一种只需要$3$次的方案。
我们先拿一根线去连接所有的黑环，这样第一次就可以染色所有的黑环。

显然，这样的话只有白环的线上部分是被多染的，我们需要将它去掉。那么我们可以在旁边再找一条线让这些地方联通。

新加的部分无论在黑环上还是白环上都是多的，显然是需要去掉的。
此时所有多了的位置都是多$1$，并且联通，再有一次操作就可以将它们都去掉了。

既然我们有了上面这种方法，我们可不可以将这种方法扩展到任意图上？
显然是可以但，当然，如果再找一条路径使得全部联通块联通也太蠢了，我们可以考虑奇偶分层，第一次染色所有的黑点与奇层的白点，第二次染色所有黑点与偶层的白点，此时所有点都被多染色了一次，所以第三次要染色全图。
显然这种方法是看起来非常合理的，毕竟任意层的内部都是联通的，但是可能会出现这样的情况，偶层都是白点，那么奇层的黑点间第一次时就不能相连了。
那么我们可以考虑加几行来进行调整。
我们将第一行与最后一行从原层中分开，第一次染色时顺便将第一行全部染完，第二次染色时顺便将第二行全部染完，第三次只去掉第一行与第二行中原本就是黑色的部分就可以了。
当然如果总共就两行当然是不行的，但此时我们可以将整张图翻转一下嘛。

显然，以我们上面的方案可以在$\min (n,m)>1\wedge \max (n,m)>2$的时候构造出答案为$3$合法解。
如果$\min (n,m)=1$的话，答案就是黑色连通块的个数嘛。
如果$n=2,m=2$，就可以手玩出解了。
如果原本答案比$3$小的话，也就是说答案为$2$或者$1$。
为$1$的话说明原来只有一个连通块，为$2$的话说明某个白色联通块可以串联起所有黑色的联通块，这两者都可以特判。
然后，就完成啦。

时间复杂度$O\left(\alpha nm\right)$。

源码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> pii;
#define MAXN 250005
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
template<typename _T>
void read(_T &x)
	_T f=1;x=0;char s=getchar();
	while(s<'0'||s>'9')if(s=='-')f=-1;s=getchar();
	while('0'<=s&&s<='9')x=(x<<3)+(x<<1)+(s^48);s=getchar();

template<typename _T>
_T Fabs(_T x)return x<0?-x:x;
int add(int x,int y,int p)return x+y<p?x+y:x+y-p;
void Add(int &x,int y,int p)x=add(x,y,p);
int qkpow(int a,int s,int p)int t=1;while(s)if(s&1)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1;return t;
int n,m,fa[MAXN],id[505][505],idx,cnt,ip[MAXN],val[MAXN];
int deg[MAXN],sum[2],ans[505][505],sta[MAXN],stak;
bool vis[MAXN];
char maze[505][505];
int dx[5]=1,-1,0,0,dy[5]=0,0,1,-1;
vector<pii>vec[MAXN],A[4][2];
void makeSet(int x)for(int i=1;i<=x;i++)fa[i]=i;
int findSet(int x)return fa[x]==x?x:fa[x]=findSet(fa[x]);
void unionSet(int a,int b)int u=findSet(a),v=findSet(b);if(u^v)fa[u]=v;
void work(vector<pii> tmp)
	int siz=tmp.size();
	for(int i=0;i<siz;i++)
		ans[tmp[i].fir][tmp[i].sec]=1;

void print()
	for(int i=1;i<=n;i++,puts(""))
		for(int j=1;j<=m;j++)
			printf("%d",ans[i][j]),ans[i][j]=0;

int main()
	freopen("bitbit.in","r",stdin);
	freopen("bitbit.out","w",stdout);
	read(n);read(m);
	for(int i=1;i<=n;i++)scanf("\\n%s",maze[i]+1);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			id[i][j]=++idx;
	makeSet(idx);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			for(int k=0;k<4;k++)
				int tx=i+dx[k],ty=j+dy[k];
				if(tx<1||tx>n||ty<1||ty>m)continue;
				if(maze[i][j]!=maze[tx][ty])continue;
				unionSet(id[i][j],id[tx][ty]); 
			
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			if(findSet(id[i][j])==id[i][j])
				ip[id[i][j]]=++cnt,val[cnt]=maze[i][j]-'0';
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			id[i][j]=ip[findSet(id[i][j])],
			vec[id[i][j]].pb(mkpr(i,j));
	for(int i=1;i<=cnt;i++)sum[val[i]]++;
	if(!sum[1])puts("0");return 0;
	if(min(n,m)==1)
		printf("%d\\n",sum[1]);
		for(int i=1;i<=cnt;i++)if(val[i])
			puts("+"),work(vec[i]),print();
		return 0;
	
	if(sum[1]==1)
		puts("1");
		for(int i=1;i<=cnt;i++)
			if(val[i]==1)puts("+"),work(vec[i]),print();
		return 0;
	
	for(int i=1;i<=cnt;i++)if(!val[i])
		int siz=vec[i].size();
		for(int j=0;j<siz;j++)
			int ax=vec[i][j].fir,ay=vec[i][j].sec;
			for(int k=0;k<4;k++)
				int tx=ax+dx[k],ty=ay+dy[k],z;
				if(tx<1||ty<1||tx>n||ty>m)continue;
				if((z=id[tx][ty])==i)continue;
				if(vis[z])continue;vis[z]=1;sta[++stak]=z;
			
		
		deg[i]=stak;while(stak)vis[sta[stak--]]=0;
		if(deg[i]==sum[1])
			puts("2");
			for(int j=1;j<=cnt;j++)if(val[j])work(vec[j]);
			work(vec[i]);puts("+");print();puts("-");work(vec[i]);print();
			return 0;
		
	
	if(n!=2)
		for(int i=1;i<=m;i++)A[2][maze[1][i]-'0'].pb(mkpr(1,i));
		for(int i=2;i<n;i++)
			for(int j=1;j<=m;j++)
				A[j&1][maze[i][j]-'0'].pb(mkpr(i,j));
		for(int i=1;i<=m;i++)A[3][maze[n][i]-'0'].pb(mkpr(n,i));
	
	else
		for(int i=1;i<=n;i++)A[2][maze[i][1]-'0'].pb(mkpr(i,1));
		for(int i=1;i<=n;i++)
			for(int j=2;j<m;j++)
				A[i&1][maze[i][j]-'0'].pb(mkpr(i,j));
		for(int i=1;i<=n;i++)A[3][maze[i][m]-[硫化铂]传染

 [硫化铂]密码
 [硫化铂]treecnt
 [硫化铂]卿且去
 [硫化铂]好
 [硫化铂]未来