Mina中的Kimchi SNARK

Posted 2022-03-25 mutourend

1. 引言

Mina系列博客有：

• Mina概览
• Mina的支付流程
• Mina的zkApp
• Mina中的Pasta（Pallas和Vesta）曲线
• Mina中的Schnorr signature
• Mina中的Pickles SNARK

Mina计划将其proof system由Pickles省级为Kimichi。Kimchi生成的递归证明时Mina链保持为约22KB的固定大小，且未来将随着zkApps升级支持隐私智能合约。

Kimchi升级之后，将支持faster provers, larger circuits以及可能更短的proof size。
详细的Kimchi代码实现见：

• https://github.com/o1-labs/proof-systems（Rust语言）

视频解说见：

• David Wong PLONK系列视频How does PLONK work?

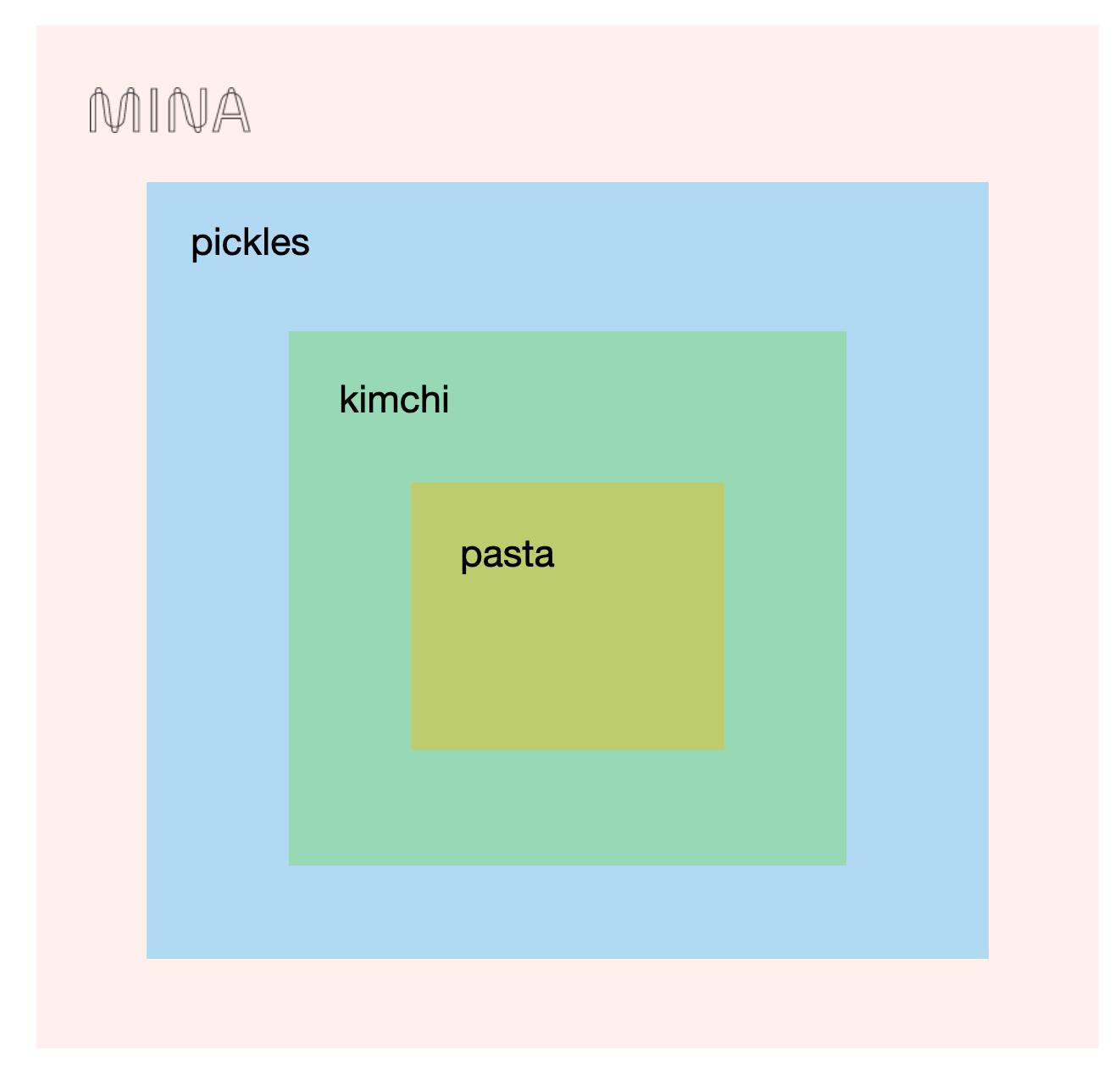
Pickles为Mina的递归层，可使用Pickles协议来创建proofs of proofs of proofs of … 来将区块链reduce为小于22KB的固定大小。
Pickles中使用Kimchi来创建证明，而Kimchi中采用ZCash Halo的pasta曲线：

2. 何为Kimchi？

Kimchi是基于Gabizon等人2019年发布的PLONK论文。基于该论文，人们提出了许多改进和扩展。有fflonk、turbo PLONK、ultra PLONK、plonkup和最近的plonky2。很难理解，但基本上所有这些协议都实现了PLONK的变体。因此，我们称之为“plonkish的协议”。Kimchi也是类似的plonkish协议。

如今，PLONK被认为是最具雄心的通用零知识证明结构之一。许多项目对PLONK做了实现，如：

• ZCash的Halo2
• Polygon Zero（以前称为Mir Protocol）的Plonky和Plonky2
• Aztec Network的PLONK+PLOOKUP
• Dusk Network的PLONK 和 PLONKUP
• MatterLabs（zksync）以Solidity实现的 Kate commitment based PLONK recursive aggregation circuit 和 Solidity verifier for Plonk
• Astar Network基于Dusk版本的PLONK进行了扩展
• anoma基于Dusk版本的PLONKUP进行了扩展

2.1 何为证明系统？

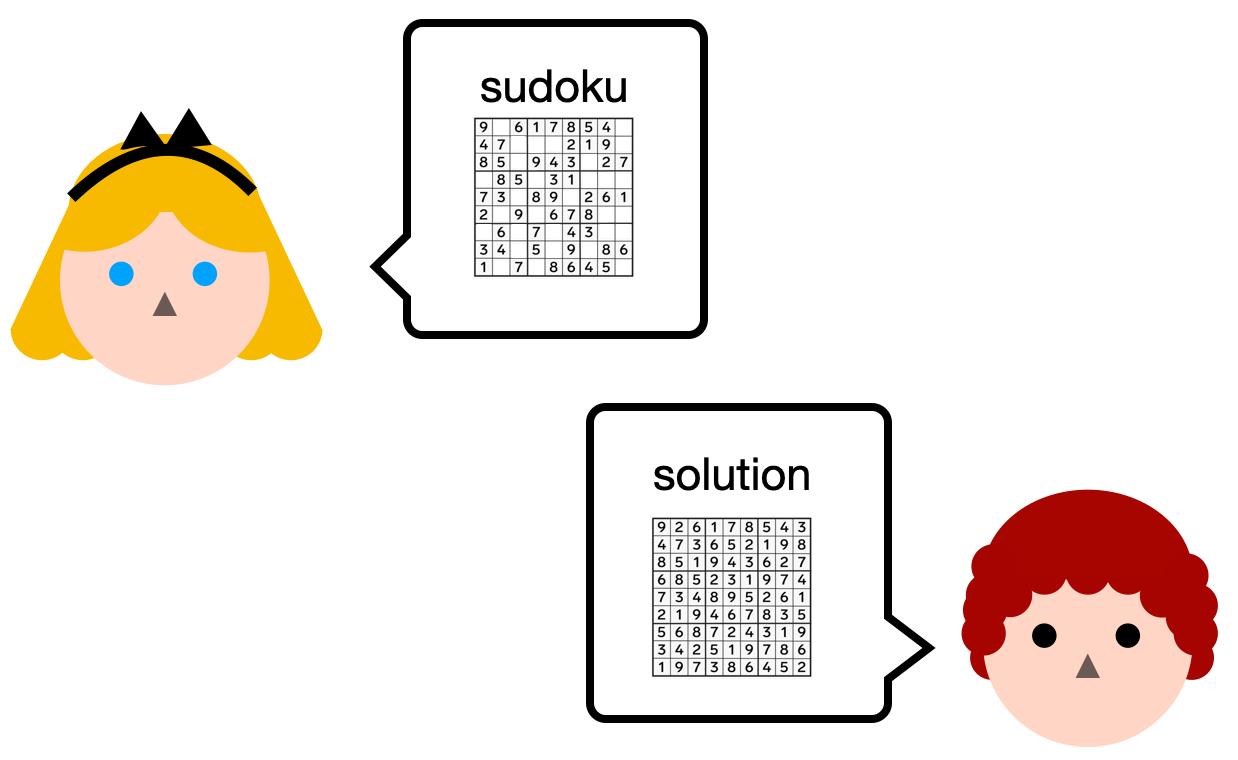
假设Alice将数独题 发送给Bob，有2种方式：

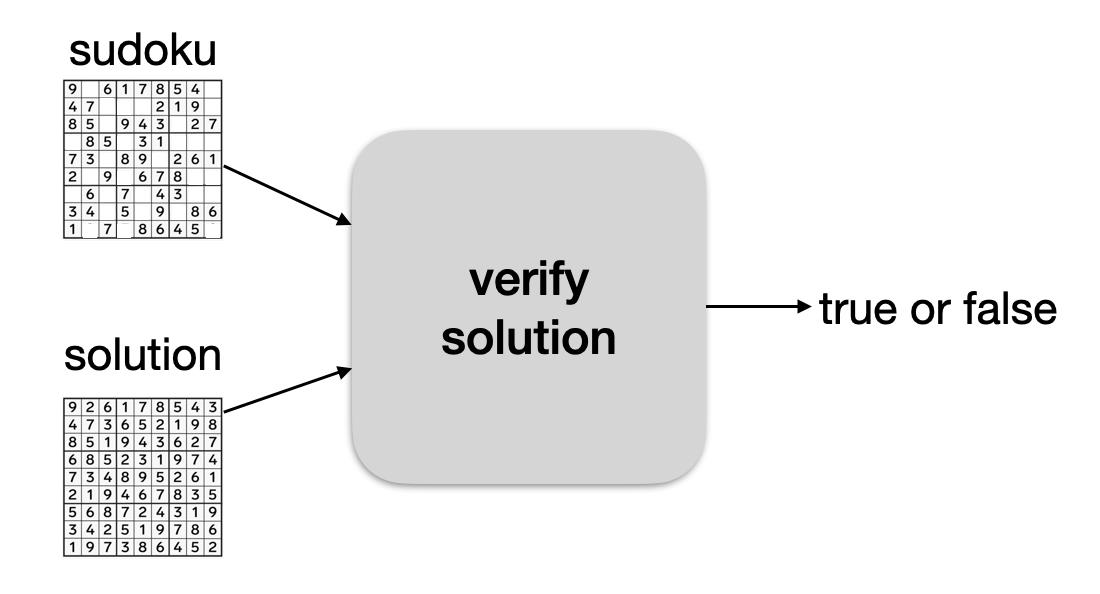
• 1）Bob直接将该题的解发送给Alice，Alice运行verify solution确认Bob的解是否正确，若正确则返回true。
  
  

• 2）若Bob不想将具体的解告诉Alice，则其需要向Alice证明：”I know a solution, trust me, I just ran the verify solution program on my laptop and it returned true“。
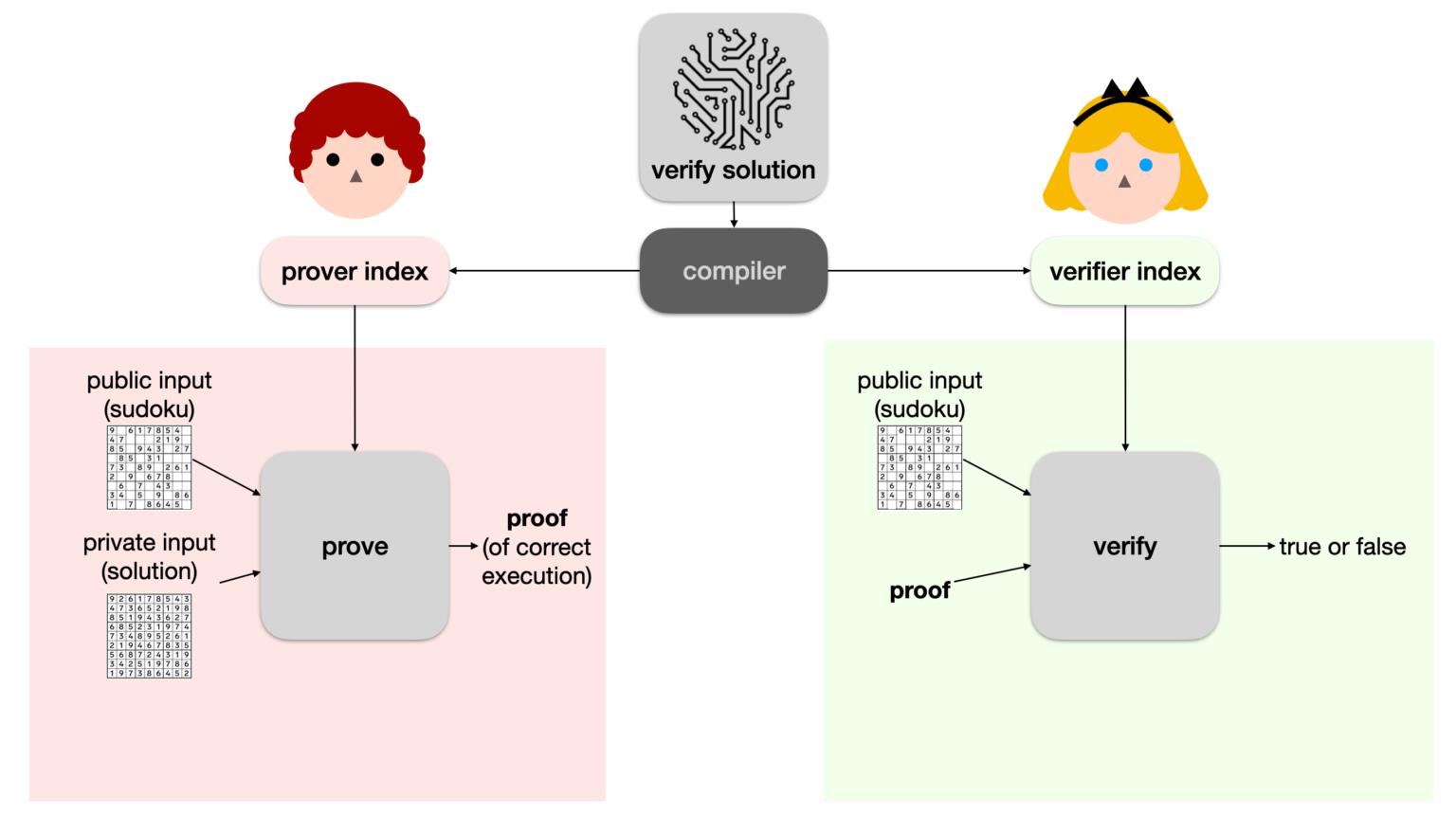
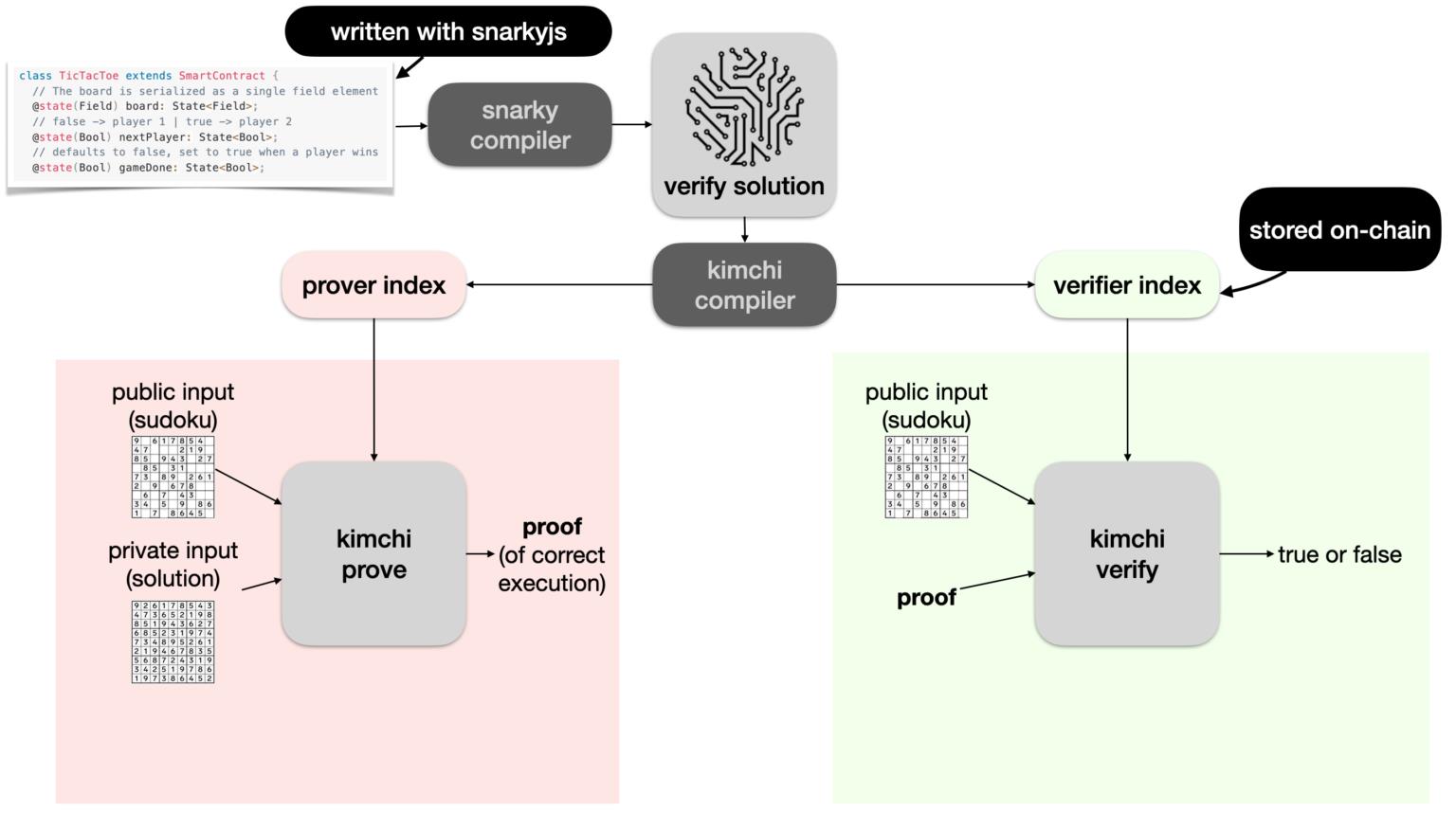
  Alice无需信任Bob。为此，可借助PLONK来实现。首先将verify solution程序分为2部分：

  • Prover index（有时命名为prover key，尽管其不是密钥）：Bob运行prove算法，该算法的输入为Prover key、数独题和解，输出为a proof。
  • Verifier index（有时命名为verifier key，尽管其不是密钥）：Alice运行verify算法，该算法的输入为Verifier key、数独题和proof，输出为true/false。
    

2.2 何为zkApps？

Mina中的zkApps（零知识智能合约）采用snarkjs来编写，然后用snarky编译成某种中间表示形式。

Kimchi编译器可将program编译为：

• prover index：用于生成proof。
• verifier index：用于验证proof。

其中verifier index会上传到链上，允许任何人验证交易中包含的proof，以确认the claim that they executed a zkApp correctly。

2.3 计算电路

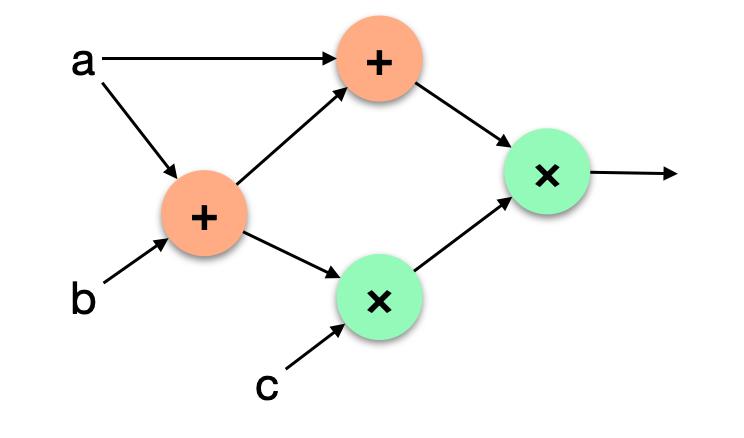
计算电路为由计算门组成的电路。


假设在某计算中需用到bit $x$，则首先需确保$x$确实是一个bit（即要么为0，要么为1），即满足约束：
$x(1-x)=0$
写电路即为写类似这样的约束，该电路可以2个门来表示：【乘法门的输出必须为0】

在PLONK中，可将其写为作用于寄存器（两个输入L和R，以及输出O）的门列表：

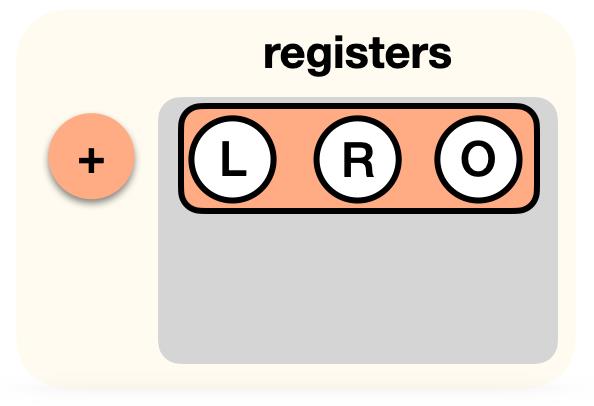
不过，上例中的加法门不是$L+R$，而是$1+(-R)$，无需额外引入”add with constant gate“或者”subtract gate“，而是将现有的加法门调整为：

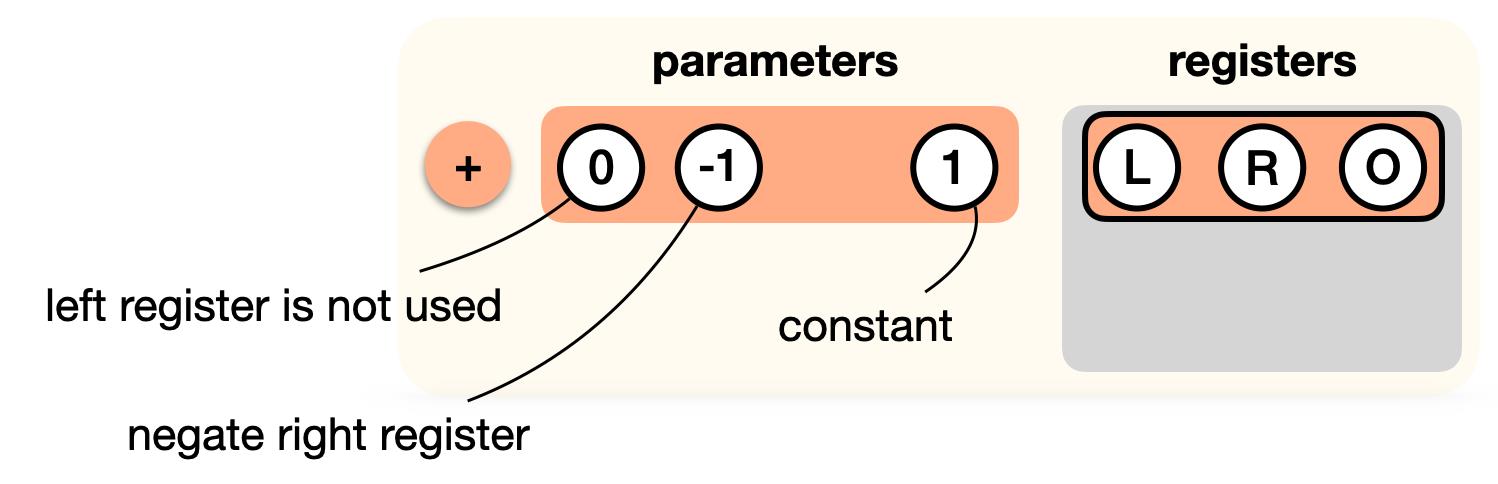
由于上例中乘法门的输出必须为0，其output register并未使用，所以将乘法门调整为：

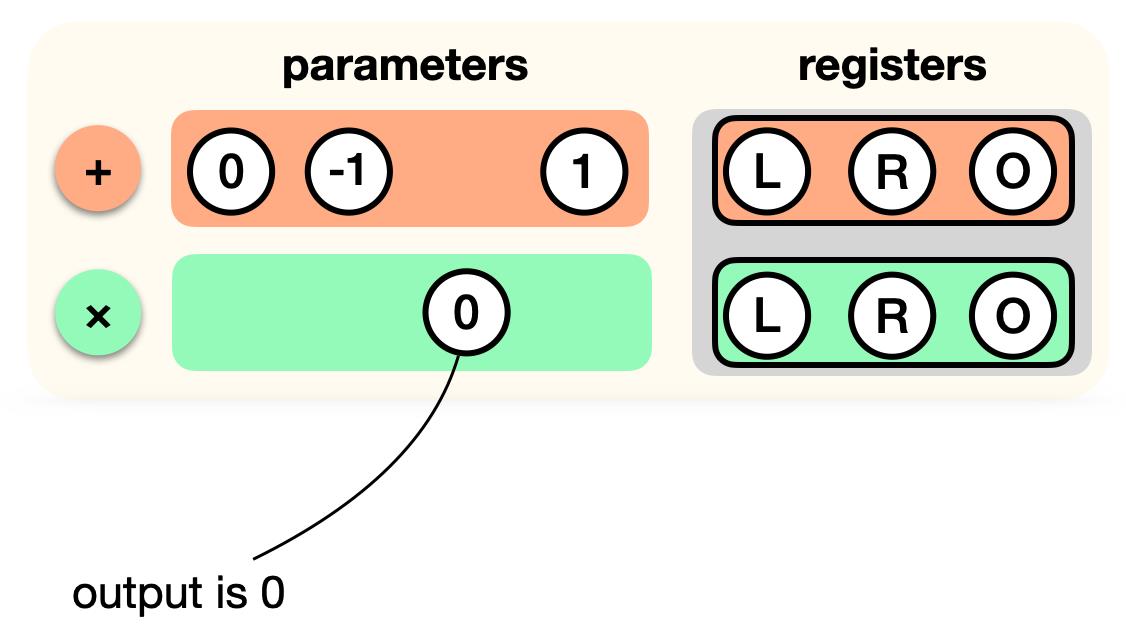
另外，由于第一个加法门的output register为第二个乘法门的left register，需要将这2个寄存器以wire连接来表示对应关系：

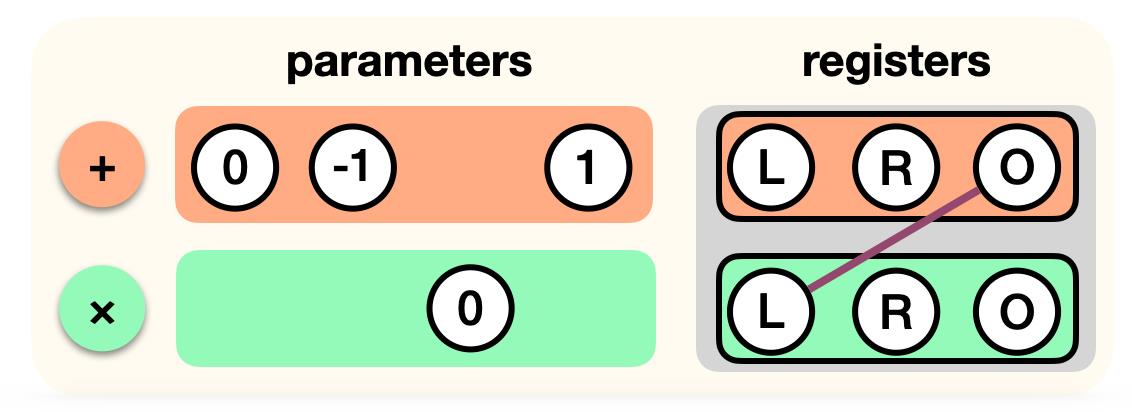
这就是在PLONK中表示电路的方式。以上已列出了所有的门（和相应的参数）以及寄存器之间的wire连接关系。

当Prover想要生成proof时，Prover需运行程序并在每个execution trace中记录每个寄存器的值。以$x=0$为例：【注意，由于第一个门的左就差你器和第二个门的输出寄存器可为人一直，因为其实际并未使用。】

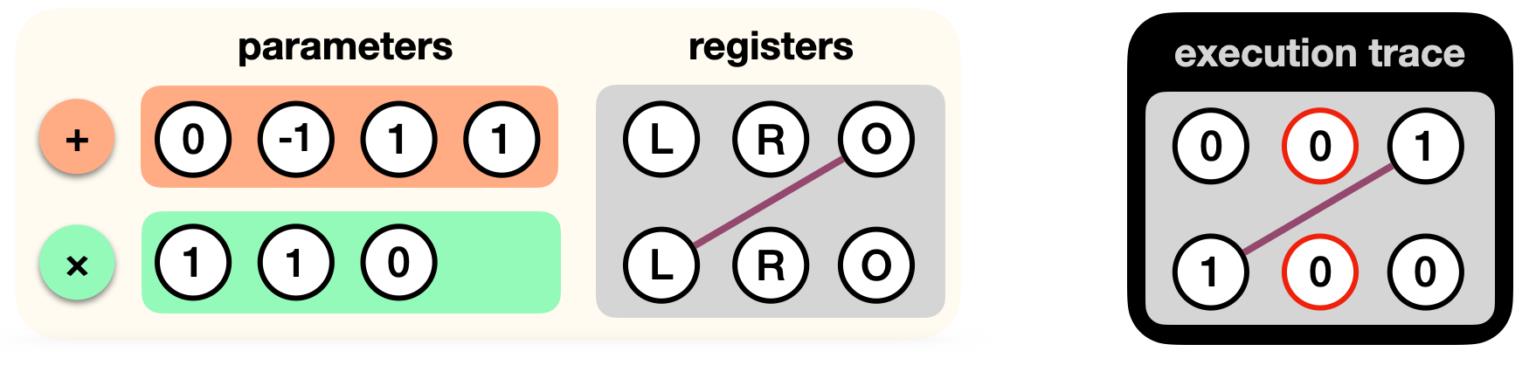
Kimchi为简化表示，在实际circuit中，上图execution trace中的右寄存器wire 连接到 之前包含value $x$的另一寄存器（或者为circuit的private input或public input）：

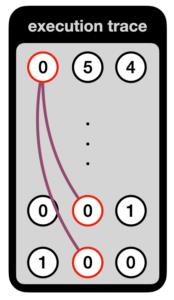
Kimchi中另一个简化是不以加法门和乘法门分别表示，而是调整为通用门：

可通过对通用门的参数进行调整来实现不同的门逻辑：

• 加法逻辑
• 乘法逻辑
• 与常量相加逻辑
• 减法逻辑
  

详细也可参看PLONK论文中的constraint定义：

2.4 由PLONK到Kimchi

Kimchi是在PLONK基础上进行的改进、优化和修改的集合。例如，通过在协议内部使用Bulletproof形式的多项式承诺，克服了PLONK的可信设置限制。这样，就不需要相信受信任设置的参与者是诚实的（如果他们不是，他们可能会破坏协议）。电路，因为我们在这里讨论电路方面，Kimchi在PLONK已经拥有的3个寄存器的基础上增加了12个寄存器：

这些寄存器分为2大类：

• IO寄存器：可相互wire连接。
• 临时寄存器（有时又称为advice wire）：仅可由关联的门使用。

更多的寄存器意味着门的输入数将多于1个：

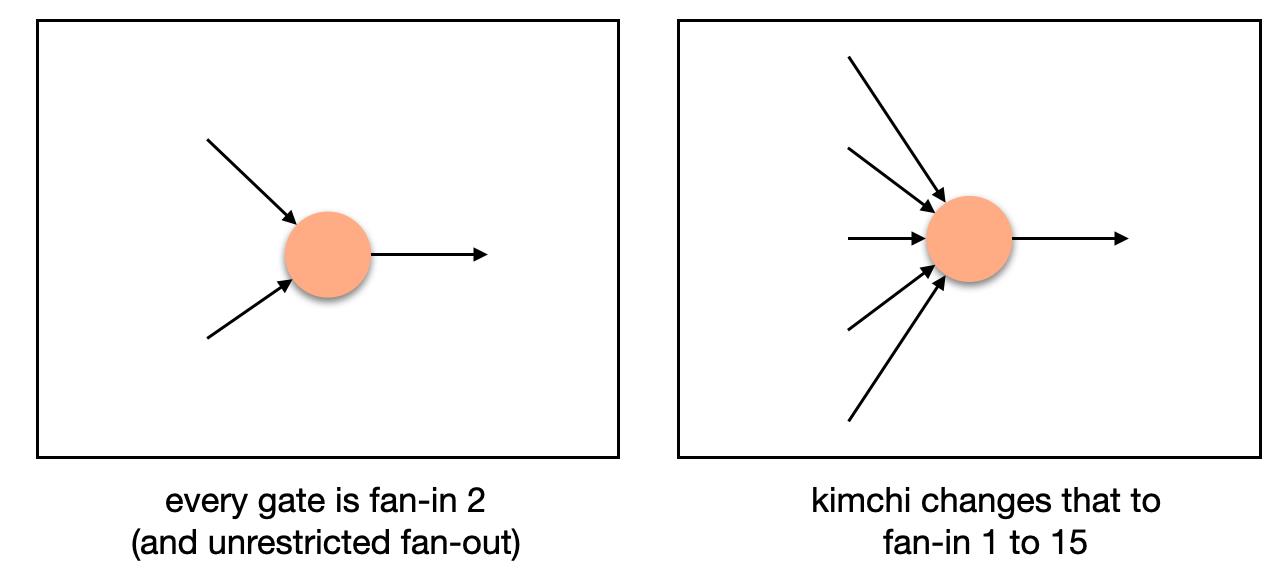
更多的输入意味着更多的可能性。以scalar multiplication为例，其至少需要3个输入（1个scalar值，以及curve point的2个坐标值），当支持更多的输入时，可实现效率更高的new gate。
本文发布时，Kimchi中实现了9种新gate：

• 1）poseidon哈希函数
• 2）椭圆曲线运算之scalar mul
• 3）椭圆曲线运算之complete add
• 4）椭圆曲线运算之endo scalmul
• 5）椭圆曲线运算之endo scalar
• 6）加密运算之chacha0
• 7）加密运算之chacha1
• 8）加密运算之chacha2
• 9）加密运算之chacha final
  

Kimchi中的另一概念是，一个门可直接将其输出写入到下一个门使用的寄存器中。这对于类似”poseidon“的门来说很有用，可在一行中使用多次（具体为11次）来表示poseidon哈希函数：

Kimchi中的另一个性能改进在于lookups。某些运算可以table表示，如XOR table为：

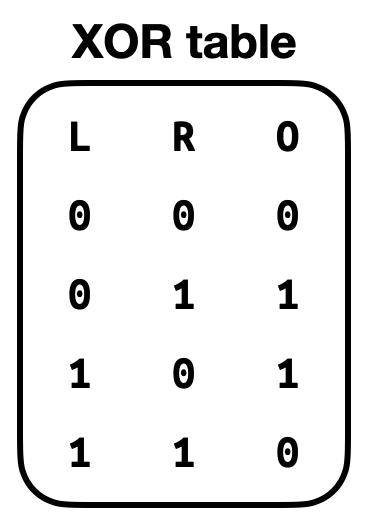
4 bits值的XOR table size为$2^8$，若以通用门来实现可能不容易且很长，为此，Kimchi构建了table，允许门（目前只有Chacha需要用到）简单地运行a lookup into the table来获取该运算的结果。

参考资料

[1] 2022年2月博客 Kimchi: The latest update to Mina’s proof system