[机器学习与scikit-learn-33]:算法-回归-通过PolynomialFeatures实现数据的升维
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[机器学习与scikit-learn-33]:算法-回归-通过PolynomialFeatures实现数据的升维相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/123591729
目录
前言:
我们常听说降维打击,这是指,在高维度空间可以轻松地实现对低维度空间的打击。本文讲展示这里说法背后的数学原理。先阐述低维空间的非线性数据分布;然后阐述用线性拟合无法解决非线性数据拟合;然后再通过升维度,把原始的数据提升到三维空间;最后在高纬度的三维空间,通过简单的线性拟合,就可以实现对非线性数据的完美拟合,最终的效果是:高维度可以轻松解决低纬的难题。
这不仅仅是数学问题,也是哲学问题:在低维度的一团麻,在低维度的无规律性,转换到高纬度后,就是一个线性问题,一目了然。
PolynomialFeatures多项项式变换就是这样的一种升维手段,其理论基础就是:任何非线性函数,都可以通过多项式来进行无限逼近,也就是说,只要数据分布是有内在规律的,就一定可以通过多项式进行拟合,除非数据内部没有任何规律。
第1章 低纬度空间(二维)的非线性样本数据分布
# 1. 导入所需要的库
# 导入所需要的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
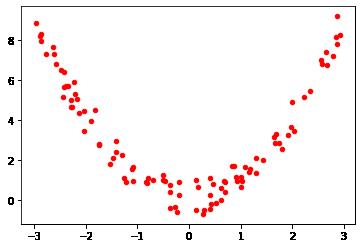
# 创建需要拟合的非线性分布数据集
#设置随机数种子
rnd = np.random.RandomState(0)
#random.uniform,从输入的任意两个整数中取出size个随机数
x1 = rnd.uniform(-3, 3, size=100)
#生成y的思路:先生成目标函数,然后再人为添加噪音
#random.normal,生成size个服从正态分布的随机数
# y和x的关系是非线性关系:二次函数关系
y = np.power(x1,2) + rnd.normal(size=len(x1))/2
#使用散点图观察建立的数据集是什么样子
plt.scatter(x1, y,marker='o',c='r',s=20)
plt.show()
第2章 用线性模型拟合拟合非线性分布数据的困难
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
# 使用原始数据进行建模
#使用原始数据进行建模
# (1) 普通线性模型
LinearR = LinearRegression() # 创建模型
LinearR = LinearR.fit(x1.reshape(-1,1), y) # 训练模型
# 可是化拟合效果
#放置画布
fig, ax1 = plt.subplots(1)
#创建测试数据:一系列分布在横坐标上的点
line_x = np.linspace(-3, 3, 100, endpoint=False).reshape(-1, 1)
#将测试数据带入predict接口,获得模型的拟合效果并进行绘制
ax1.plot(line_x, LinearR.predict(line_x), linewidth=2, color='red',label="linear regression")
#将原数据上的拟合绘制在图像上
ax1.plot(x1, y, 'o', c='k')
#其他图形选项
ax1.legend(loc="best")
ax1.set_ylabel("Regression output")
ax1.set_xlabel("Input feature")
ax1.set_title("Result before discretization")
plt.tight_layout()
plt.show()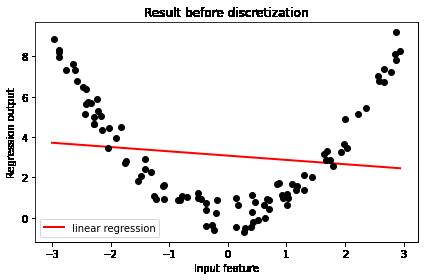
问题:
二维平面上的直线,无法拟合二维片面上的非线性的曲线。
第3章 对非线性分布数据进行升维(三维空间)
3.1 什么是升维
# 升维,把低维度的非线性关系,转换成高维度的非线性关系:
# 图形形状不变,但空间角度发生变化
import numpy as np
import matplotlib.pyplot as plt
# 创建需要拟合的非线性分布数据集
#设置随机数种子
rnd = np.random.RandomState(0)
#从输入的任意两个整数中取出size个随机数
# 原始离散数据
x1 = rnd.uniform(-3, 3, size=100)
#生成y的思路:先生成目标函数,然后再人为添加噪音
#random.normal,生成size个服从正态分布的随机数
# x2和x1在二维平面上是非线性关系:x2 = x1^2
x2 = np.power(x,2) + rnd.normal(size=len(x))/2
# 见可视化图形:
# 转换后,x2和x1的非线性关系不变
# 转换后,y与x1,x2在三维空间上是线性关系:y = x1 + x2
# 转换后,就可以在三维空间上通过线性函数拟合二维空间的非线性关系
# 升维:就是增加一个维度的特征,就可以把复杂问题(非线性问题)简单化(线性问题)
# 这就是增加维度后的神奇效果
y = x1 + x2
ax = plt.subplot(projection = '3d')
# 设置本图名称
ax.set_title('3d_image_show')
# 绘制数据点 c: 'r'红色,'y'黄色,等颜色
ax.scatter(x1, x2, y, c = 'r')
ax.set_xlabel('X1') # 设置x坐标轴
ax.set_ylabel('X2') # 设置y坐标轴
ax.set_zlabel('Y') # 设置z坐标轴
plt.show()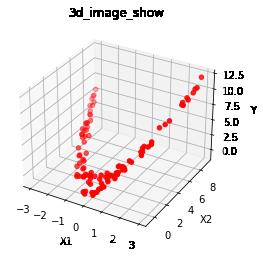
备注:
升维后,为三维空间的平面。
3.2 升维的本质
# 升维,把低维度的非线性关系,转换成高维度的非线性关系:
# 图形形状不变,但空间角度发生变化
import numpy as np
import matplotlib.pyplot as plt
# 创建需要拟合的非线性分布数据集
#设置随机数种子
rnd = np.random.RandomState(0)
#从输入的任意两个整数中取出size个随机数
# 原始离散数据
x1 = rnd.uniform(-3, 3, size=100)
#生成y的思路:先生成目标函数,然后再人为添加噪音
#random.normal,生成size个服从正态分布的随机数
# x2和x1在二维平面上是非线性关系:x2 = x1^2
x2 = np.power(x,2) + rnd.normal(size=len(x))/2
# 见可视化图形:
# 转换后,x2和x1的非线性关系不变
# 转换后,y与x1,x2在三维空间上是线性关系:y = x1 + x2
# 转换后,就可以在三维空间上通过线性函数拟合二维空间的非线性关系
# 升维:就是增加一个维度的特征,就可以把复杂问题(非线性问题)简单化(线性问题)
# 这就是增加维度后的神奇效果
y = x1 + x2
ax = plt.subplot(projection = '3d')
# 设置本图名称
ax.set_title('3d_image_show')
# 绘制数据点 c: 'r'红色,'y'黄色,等颜色
ax.scatter(x1, x2, y, c = 'r')
# 展现 y = x1 + x2的平面
x1_grid = np.arange(-4, 4, 0.01)
x2_grid = np.arange(0, 10, 0.01)
x1_grid,x2_grid = np.meshgrid(x1_grid,x2_grid)
y_grid = x1_grid + x2_grid
ax.plot_surface(x1_grid, x2_grid, x2_grid)
ax.set_xlabel('X1') # 设置x坐标轴
ax.set_ylabel('X2') # 设置y坐标轴
ax.set_zlabel('Y') # 设置z坐标轴
plt.show()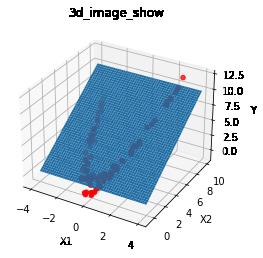
3.3 sklearn中升维方法
from sklearn.preprocessing import PolynomialFeatures
# 创建需要拟合的非线性分布数据集
#设置随机数种子
rnd = np.random.RandomState(0)
#从输入的任意两个整数中取出size个随机数
# 原始离散数据
x1 = rnd.uniform(-3, 3, size=100)
x1 = x1.reshape(-1,1)
print(x1.shape)
print(x1[0:5])
poly = PolynomialFeatures(degree=2)
y1 = poly.fit_transform(x1)
print(y1.shape)
print(y1[0:5])
# 线性拟合 y = x1 + x2
# 保留x2与x1的非线性关系
# y与x1,x2的关系是线性关系,y = x1 + x2
# y与x的关系是非线性关系: y = x1 + x1^2 =》二次项关系
# 为了在三维空间可视化需要,去掉第一列:常数项
x1 = y1[:,1:2].reshape(-1)
x2 = y1[:,2:3].reshape(-1)
print("x1.shape:", x1.shape)
print(x1[0:5])
print("x2.shape:",x2.shape)
print(x2[0:5])
y = x1 + x2
print(y.shape)
print(y[0:5])
ax = plt.subplot(projection = '3d')
# 设置本图名称
ax.set_title('3d_image_show')
# 绘制数据点 c: 'r'红色,'y'黄色,等颜色
ax.scatter(x1, x2, y, c = 'r')
# 展现 y = x1 + x2的平面
x1_grid = np.arange(-4, 4, 0.01)
x2_grid = np.arange(0, 10, 0.01)
x1_grid,x2_grid = np.meshgrid(x1_grid,x2_grid)
y_grid = x1_grid + x2_grid
ax.plot_surface(x1_grid, x2_grid, x2_grid)
ax.set_xlabel('X1') # 设置x坐标轴
ax.set_ylabel('X2') # 设置y坐标轴
ax.set_zlabel('Y') # 设置z坐标轴
plt.show()(100, 1) [[ 0.29288102] [ 1.2911362 ] [ 0.61658026] [ 0.2692991 ] [-0.4580712 ]] (100, 3) [[ 1. 0.29288102 0.08577929] [ 1. 1.2911362 1.66703268] [ 1. 0.61658026 0.38017121] [ 1. 0.2692991 0.072522 ] [ 1. -0.4580712 0.20982923]] x1.shape: (100,) [ 0.29288102 1.2911362 0.61658026 0.2692991 -0.4580712 ] x2.shape: (100,) [0.08577929 1.66703268 0.38017121 0.072522 0.20982923] (100,) [ 0.37866032 2.95816888 0.99675147 0.3418211 -0.24824198]
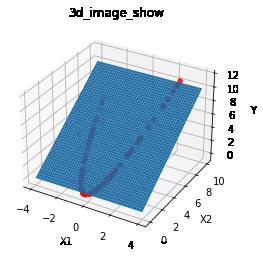
第4章 在高纬度实现对低纬度非线性分布数据的线性拟合
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
# 创建需要拟合的非线性分布数据集
#设置随机数种子
rnd = np.random.RandomState(0)
#从输入的任意两个整数中取出size个随机数
x_train = rnd.uniform(-3, 3, size=100)
print("升维前的输入特征x_train.shape:", x_train.shape)
#生成y的思路:先生成目标函数,然后再人为添加噪音
#random.normal,生成size个服从正态分布的随机数
# y和x的关系是非线性关系:二次函数关系
y_label = np.power(x1,2) + rnd.normal(size=len(x1))
print("升维前的输出标签y_label.shape:", y_label.shape)
# 创建普通线性模型:用升维前数据进行线性拟合
LinearR_initial = LinearRegression() # 创建模型
LinearR_initial = LinearR_initial.fit(x_train.reshape(-1,1), y_label) # 训练模型
# 对数据进行升维
degree = 2
poly = PolynomialFeatures(degree=degree)
X_train = poly.fit_transform(x_train.reshape(-1,1))
print("升维后的输入特征X.shape:", X_train.shape)
# 创建普通线性模型:用升维后数据进行线性拟合
LinearR_upgrade = LinearRegression() # 创建模型
LinearR_upgrade = LinearR_upgrade.fit(X_train, y_label) #训练模型
# 可是化拟合效果
# 放置画布
fig, ax1 = plt.subplots(1)
# 创建测试数据:一系列分布在横坐标上的线性点,为一维数据:(x)
x_test = np.linspace(-3, 3, 100, endpoint=False)
print("测试集的输入特征x_test.shape:",x_test.shape)
# 对测试数据集进行升维,升维后为三维数据: (x^0, x^1, x^2)
poly = PolynomialFeatures(degree=degree)
X_test = poly.fit_transform(x_test.reshape(-1,1))
print("升维后的输入特征X_test.shape:", X_test.shape)
#将测试数据带入predict接口,获得模型的预测数据
y_label
y_pred_initial = LinearR_initial.predict(x_test.reshape(-1,1))
y_pred_upgrade = LinearR_upgrade.predict(X_test)
# 绘制图像
ax1.plot(x_train, y_label, 'o', linewidth=2, color='black',label="sample data")
ax1.plot(x_test, y_pred_initial, linewidth=2, color='green',label="linear regression")
ax1.plot(x_test, y_pred_upgrade, linewidth=3, color='red', label="non-linear regression")
#设置其他图形选项
ax1.legend(loc="best")
ax1.set_ylabel("Regression output")
ax1.set_xlabel("Input feature")
ax1.set_title("Result before discretization")
plt.tight_layout()
plt.show()升维前的输入特征x.shape: (100,) 升维前的输出标签y.shape: (100,) 升维后的输入特征X.shape: (100, 3) 测试集的输入特征x_test.shape: (100,) 升维后的输入特征X_test.shape: (100, 3)
(1)degree = 2时的图像
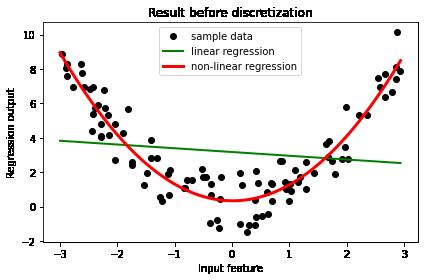
(2)degree = 10时的图像
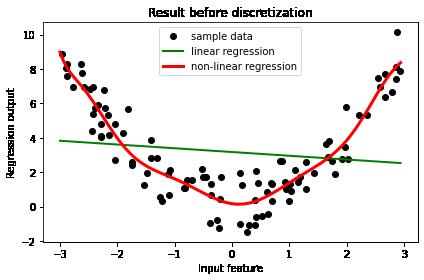
(3)degree = 20时的图像

备注:
升维的维度越高,拟合度越高,越容易过拟合。
作者主页(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/123591729
以上是关于[机器学习与scikit-learn-33]:算法-回归-通过PolynomialFeatures实现数据的升维的主要内容,如果未能解决你的问题,请参考以下文章