submodular函数优化

Posted 2022-03-22 Terry_dong

几个月之前写了一篇文本摘要任务的一些总结（详见 文本自动摘要任务的初步总结），其中在说无监督方式做抽取式摘要的时候，参考了一篇论文：A Class of Submodular Functions for Document Summarization 。最近在做业务新闻摘要的时候，基于当前无标注数据，准备应用该方法来做无监督的抽取式摘要。但是在实现的过程中，发现了很多之前忽略的细节问题，因此本篇作为上篇总结文章的补充，聚焦优化求解submodular函数的具体实现。

前情回顾

首先，简单回顾一下A Class of Submodular Functions for Document Summarization 的基本思想。submodular函数具有submodularity，它是经济学上边际效益递减（property of diminishing returns）现象的形式化描述。形象的比喻就是饿的时候吃一个包子，比八分饱的时候吃一个包子带来的满足感更强。然后我们以摘要中常见的两个度量来表示一个摘要的重要性分数，分别为相关性和冗余度。可以通过设计各种不同种类的函数来分别代表相关性和冗余度来比对提升整体方法的效果。最后我们通过一些优化算法，得到使得该函数取最大值的摘要实例。函数的设计需要满足一定的条件，具体如下：

1、函数有不等式约束条件。每次将一个摘要句子加入到摘要集合中时，通过submodular函数能够计算得到一个增益分数，同时该操作同时也会有一定的消耗cost，对于摘要来说，可以用摘要句子的个数或者摘要集合句子中的字符（字节）总数来表示cost，当整体cost累计达到一定的上界时，我们就不能再增加摘要句子了。因此cost需要满足： 

2、函数是否具有单调性。这个条件对于后续使用的优化算法有极大的影响。这也是本篇文章会着重描述的内容。下面就详细解析如何用优化算法来优化submodular函数。

有关于相关性和冗余度的函数设计详见我的上一篇总结文章，本篇不作为重点内容。

submodular函数的求解问题

论文中提到，带cost上界约束条件下的通用submodular函数最大化求解任务是一个NP难度问题。因此，在实现时，很难获取全局最优解。但是我们可以通过一些算法来获取接近最优解的次优解。贪心算法是一个应用较为广泛的算法，其逻辑简单同时也能获取接近最优的效果。通过对贪心算法的各种优化变种，我们可以对大部分的submodular函数进行求解。然而，在实际业务落地时，我们不能仅关注模型的效果，还需要关注模型的性能，尤其是在一些实时性要求较高的场景。传统贪心算法的性能是比较差的，里面包含了大量的循环计算逻辑（会包含两两句子之间的相似度计算）。因此，我们需要对贪心算法进行一些优化设计，使其在保证能够得到近似解的同时又能降低计算复杂度。事实上，一个submodular函数是否单调，对于贪心算法的设计有很大影响。

非单调的submodular函数

我们首先看一个非单调submodular函数做摘要的例子。论文中给出了MMR的例子，关于MMR（Maximal Marginal Relevance）算法，同样在我之前的文章中有详细介绍，这里就不重复描述了，仅给出其公式：

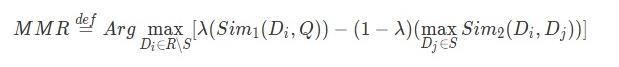
这个求解式可以转化成： 

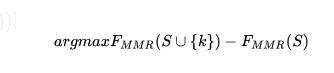
 。简单来说就是将摘要k加入到候选摘要集合后通过F函数获得的增益分数。对于MMR来说就是将候选句子Di加入到摘要集合后，整体的相关性分数会提升，但是冗余度会增加，因此需要找到使得相关性-冗余度得到最大值的句子。这里F就包含了相关性和冗余度，且是一个submodular函数。

但是这个函数显然不是一个单调函数，因此传统的最简单贪心算法无法在常数级的量级上逼近最优解，每个迭代并不能保证通过增益分数选择的句子在当前cost的条件下是最合适的（下面有具体的实例说明）。

那么，对于MMR来说，难道就不能用贪心算法来优化求解了吗？

当然可以！通过仔细阅读论文，发现该篇论文的作者在另一篇文章中，给出了一个modified的贪心算法来对MMR算法进行求解。论文链接：Multi-document Summarization via Budgeted Maximization of Submodular Functions。下面给出该算法的基本流程：

摘要集G初始化为空集set()
候选原文句子集合U初始化为原文句子集合V
已经设计好的submodular函数f,这里f(G+l)-f(G)就是MMR的表达式
每个句子添加到G中的cost，cost上界为B
while U is not empty and sum(cost(G))<=B:
     f_value_list = []
     for l in U:
        f_value_list.append((f(G+l)-f(G))/(c_l)^r)
     k = argmax(f_value_list)
     if sum(cost(G))+cost(k)<=B and (f(G+k)-f(G) >=0:
        G.add(k)
     U.remove(k)
end while
f_value_for_V_list = []
for v in V:
   if cost(v)<=B:
      f_value_for_V_list.append(f(v))
v* = argmax(f_value_for_V_list)
if f(v*) > f(G):
   return v*
else:
   return G

上述为modified greedy algrithm的伪代码。整体流程还是比较简单的，相对于原始的贪心算法，论文主要优化了以下几点：

1、这个贪心算法的最外层循环需要遍历每一个候选句子。在每个迭代中，并不一定会选择一个句子加入到摘要集合中，因此该算法的循环计算次数会比传统的原始贪心算法要多。

2、在计算候选摘要句增益得分的时候，因为每个句子的cost都不尽相同（例如句子长度，句子所在的位置等），因此需要做rescaling。该算法法在rescaling的基础上引入了r这个超参数，论文中称之为scaling factor。

3、在跳出最外层循环后，并没有立刻返回结果，而是又对原始文章中的每个句子单例进行分析，获取得分增益最大且cost满足条件的单个句子，最后将其submodular函数值与摘要集合的函数值进行比较，取最大的那个。

那么问题来了，上述几点优化的原因和目的是什么呢？

论文中提到，一个贪心算法的最核心部分在于他的启发式贪心逻辑。原始贪心算法是直接在每个迭代简单选择一个最大化分数增益（(f(G+k)-f(G))/c_k）的句子直到其累计的cost超过上界B，这样做会导致算法的approximation factor依赖于非常数项。

approximation factor指用一些近似算法求解一些NP-hard难度问题时，获取的近似最优解与原始最优解的逼近程度。对于求解最大值，0<factor<1，代表使用该算法至少能获取原始最优解factor的次优解。

approximation factor 如果依赖于非常数项会导致什么问题？例如，对于集合V=a,b,f(a)=1，f(b)=p，cost(a)=1，cost(b)=p+1，B=p+1。原始的贪心算法得到的最优函数结果为1，选择了a，而最终应当选取的最优解应当是b，其对应的最优函数结果为p（因为b的cost正好充满B）。此时，可知逼近因子为p，这个p是变量，与b的函数值相关。用非常数因子的算法做最优求解，降低了算法整体的逼近能力，使其极度依赖数据的质量。

因此论文提出了上述几个优化点，其中，第三点主要是将得到的摘要集合和单个句子实例进行比较，这一步能够保证我们在r=1时能够得到常数项的逼近因子。（详细的证明在论文的Appendix中，由于篇幅太长了，感兴趣的同学请自行查阅论文，这里就不赘述了。）

另外，上面第二点为cost的rescaling增加了一个scaling factor r。增加这个因子的作用在于能够平衡一些在选择时难以取舍的例子，比如AB两个句子，A的cost为15，其增益为2，B的cost为10，其增益为1，我们很难去界定A和B哪个更好。通过调整r，可以帮助某一方的选择权重得到提升。当然这个超参数我在实际验证的时候取1一般就可以，如果有验证集的话，可以通过验证集来调整这个超参数。

单调的submodular函数

虽然上述基于MMR的submodular函数被证明能够以常数项逼近因子获得接近最优解的解，但是显然这种情况不会对所有的非单调submodular都成立。因此，将submodular函数设计成单调的对于高效应用贪心算法来说就显得很有意义了。这也是A Class of Submodular Functions for Document Summarization 中将冗余度函数设计成奖励多样性函数，使得其和相关性函数共同组成一个单调submodular函数的原因。对于单调的submodular函数而言，必定能通过贪心算法，以常数项因子逼近最优解。

至此，我们已经能够基本实现submodular算法抽取摘要的核心内容。然而事情并没有结束，从上述算法逻辑可知，这种贪心算法的性能是较低的，因为它的最外层循环是遍历所有的候选句子，而且最后还要做对句子单例做循环计算。那么有没有更加高效的算法能够接近其效果，同时提升性能呢？

经过一些调研，我主要发现了两个优化版本的贪心算法，分别是lazy greedy 以及stochastic greedy。这两个算法都是针对单调submodular函数在原始贪心算法基础上进行的优化。

lazy greedy algorithm

lazy greedy算法主要是利用了单调submodular的单调性。论文链接：Cost-effective Outbreak Detection in Networks 。其核心流程如下：

摘要集G初始化为空集set()
候选原文句子集合U初始化为原文句子集合V
已经设计好的submodular函数f,这里f(G+l)-f(G)就是MMR的表达式
每个句子添加到G中的cost，cost上界为B
f_value_for_each_sentence = l:100 for l in V //对每个句子初始化一个极大的f_value值
first_update=True
while U is not empty and sum(cost(G)) <=B:
     if first_update
        计算f(G+l)-f(G) for each l in U
        更新f_value_for_each_sentence for each l in U
        s* = argmax(f_value_for_each_sentence[U])
        if s* >=0:
            G.add(s*)
            U.remove(s*)
        first_update=False
     else:
        sorted_f_value = sorted(f_value_for_each_sentence,reverse=True)
        更新sorted_f_value中的最大值对应的句子的新f_value，看其新的value是否仍然是最大
        if f_value is max and f_value >=0 :
           将该句子添加到G中，从U中删除该句子
        else:
           按照大小依次执行上述操作，直到找到一个f_value为最大的值，将对应句子更新到摘要集合中
            

上述算法优化的地方在于每个迭代不一定会计算所有句子的增益分数。而是先将U中第i-1个迭代计算后的分数列表先进行由大到小的排序，在选取最大值对应的句子后，增益分数第二大的句子就成为了第i个迭代中的最大值，假设为A。在第i迭代计算时，优先对A先进行增益分数的更新计算，根据单调submodular函数的单调性可知，该句子极有可能仍然是目前U中最大的值。

当然，lazy greedy算法虽然在一定程度上提升了贪心算法的效率，但是它本质上却没有改变贪心算法的复杂度。在最坏情况下，每轮迭代中lazy greedy仍然需要计算所有U中句子的增益分数（更新增益分数后，直到U中最后一个句子才找到最大值）。

stochastic greedy algrithm

该算法相比于lazy greedy是真正优化了贪心算法的复杂度。其论文链接：Lazier Than Lazy Greedy 。它的算法核心思想非常简单，在原始贪心算法的基础上，在每轮迭代计算时，并不是对U中所有的句子都进行处理，而是随机采样一个子集，对这个子集进行循环计算。其中，引入一个超参数 

小结

本篇文章主要聚焦在如何对submodular函数进行最优解求解。探讨了几种贪心算法的变种，均能够以常数因子逼近最优解。其中，探讨了stochastic greedy以及lazy greedy方法，提升了贪心算法的性能，使得其能够应用在实际业务中。

题外话

通过这次在业务中的实践，发现了自己在之前的论文研究和实现中忽略了很多细节。之前在实现这篇论文方法的时候，只关注了如何去设计相关性和多样性的建模函数，对于如何去优化求解这个函数直接就用了原始贪心算法，完全没考虑其是否能够得到逼近最优解的次优解，也没考虑其算法的性能问题。深入研究后，才发现其中的技术细节还有很多需要探讨。在之后的研究中，还是要关注细节，并通过实践去了解一个技术点的全貌。