深度学习4. 单层感知机概念及Python实现

Posted 2023-03-13 编程圈子

深度学习4. 单层感知机概念及Python实现

• 一、概念
• 二、数学表达
• • 1. 数学公式
  • 2. 单层感知机示例
• 三、单层感知机Python实现关键知识点
• • 1. 生成样本特征矩阵
  • 2. 生成标签y
  • 3. 训练迭代
  • 4. 学习率
  • 5. 计算预测值
  • 6. 更新权重
  • 7. 更新偏置
  • 8. 绘制决策边界
• 四、Python完整实现

一、概念

感知机（Perceptron）是神经网络中的一个概念，在1958年由Frank Rosenblatt第一次引入。
单层感知机可以用来区分线性可分的数据，并且一定可以在有限的迭代次数中收敛。

感知机作为一种基本的神经网络模型，它模拟了人脑神经元的工作原理。感知机接受多个输入信号，将它们加权求和并加上偏置值，然后通过一个激活函数将结果转化为输出信号。

感知机可以用于分类问题，将输入信号分为不同的类别。

感知机是神经网络的基本组成单元，通过多个感知机的组合可以构建更加复杂的神经网络模型，如多层感知机（MLP）和卷积神经网络（CNN）等。

感知机是用数学方式模拟人体神经网络结构。

人体神经网络

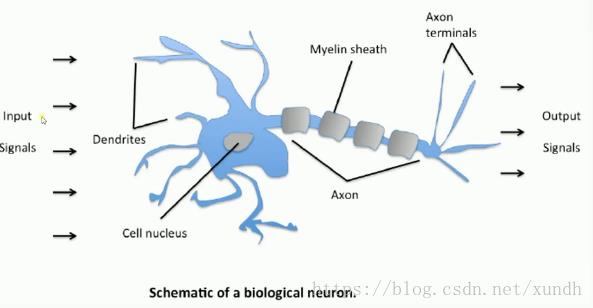
单层感知机 模拟人体神经网络：
单层感知机（Single Layer Perceptron）是最简单的神经网络。它包含输入层和输出层，而输入层和输出层是直接相连的。

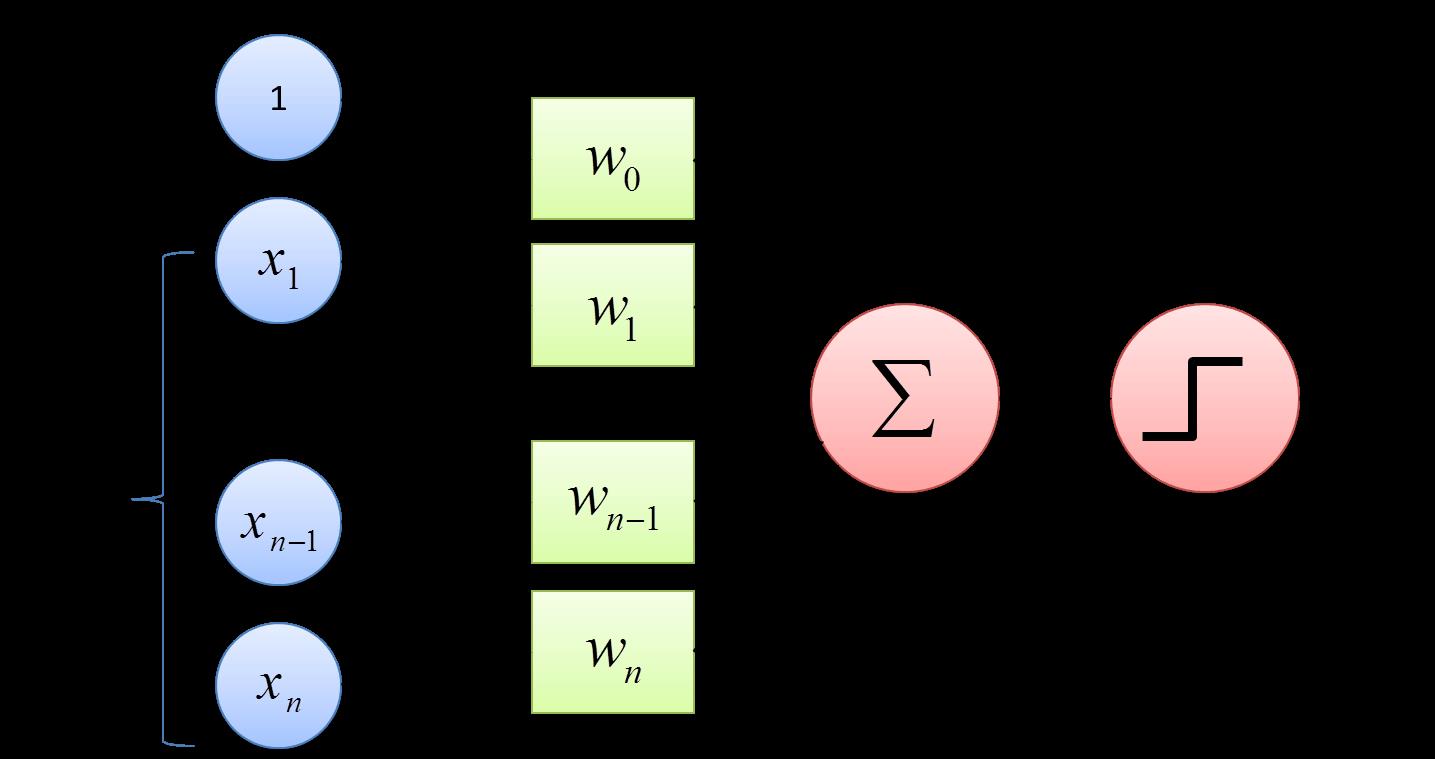
上图中 x1, x2, ……, xn是输入层，将x1与权重w1相乘， x2与权重w2相乘， x3与权重w3相乘……，加上偏置，把结果相加，再经过一个激活函数，输出结果。

二、数学表达

1. 数学公式

感知机的基本原理可以用以下公式表示：

$$y=f(w1x1+w2x2+...+wn\ast xn+b)$$

其中，x1, x2, …, xn是输入信号，w1, w2, …, wn是对应的权重，b是偏置值，f是激活函数，y是输出信号。

感知机的学习过程可以通过不断调整权重和偏置值来完成。一般采用梯度下降算法，通过最小化损失函数来优化权重和偏置值。常用的损失函数包括均方误差和交叉熵等。

2. 单层感知机示例

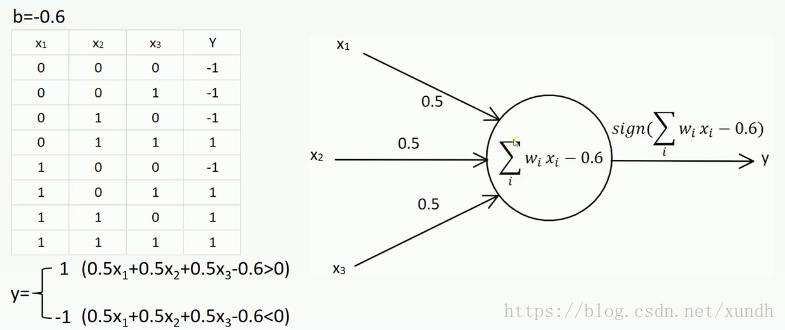
把偏置当做特殊可能权值：

这时把x₀固定为1，取消权值，以减化运算。

三、单层感知机Python实现关键知识点

1. 生成样本特征矩阵

X = np.random.randn(100, 2)

生成一个100行2列的随机数矩阵，其中每个元素都是从标准正态分布（均值为0，方差为1）中随机采样得到的。也可以理解为在二维空间中随机生成100个点，这些点的横坐标和纵坐标都是从标准正态分布中随机生成的。这是用于训练单层感知机的样本特征矩阵，每行代表一个样本的特征，每列代表一种特征。

2. 生成标签y

y = np.array([1 if x1 + x2 >= 0 else -1 for x1, x2 in X])

根据输入数据 X 生成对应的标签 y。其中 x1 和 x2 分别表示样本的两个特征，这里的目的是为了生成一个二分类任务的标签，使得单层感知机可以通过学习来对样本进行分类。

最终得到的 y 是一个包含100个元素的一维数组，其中每个元素是1或-1，表示对应样本的标签。

3. 训练迭代

将要定义一个训练函数 perceptron，使用变量n_iter表示迭代次数。每迭代一次，感知机会用当前的权重对样本进行预测，并计算预测值与真实标签之间的误差。然后根据误差值来调整权重，以期望能够使预测结果更加接近真实标签。
n_iter 值越大，训练时间越长，可能会使得感知机的性能提高，但也会增加过拟合的风险。在实际应用中，我们需要根据具体情况来调整 n_iter 的值。

def perceptron(X, y, lr=0.1, n_iter=100):

4. 学习率

学习率控制了每次参数更新的步长，即每次参数更新时改变的大小。
在单层感知机中，学习率决定了每次更新权重和偏置的步长。

• 如果学习率过大，每次更新的步长就会很大，可能会导致权重和偏置跳过了最优解，导致模型无法收敛。
• 如果学习率过小，每次更新的步长就会很小，可能会导致模型收敛速度过慢，需要更多的迭代次数才能收敛到最优解。

在单层感知机中，选择合适的学习率是非常重要的。通常可以使用网格搜索或随机搜索等方法来搜索最优的学习率。另外，还可以使用自适应学习率的方法，如 Adagrad、Adadelta、Adam 等，自动调整学习率大小，以提高模型的训练效果。

5. 计算预测值

这里会使用 np.dot(weights, X[i]) 将权重 weights 和第 i 个样本 X[i] 做向量内积，即将权重矩阵和样本特征向量相乘。
weights 是一个包含两个元素的一维数组，每个元素对应着一个特征的权重，X[i] 是一个包含两个元素的一维数组，每个元素对应着样本的一个特征。内积操作相当于将两个向量的对应元素相乘，再将乘积相加得到一个标量值。

然后加上偏置值 bias，即得到 y_pred，表示感知机对第 i 个样本的预测结果。这里的 bias 是一个标量值，它用来调整感知机的阈值，即当 y_pred 大于等于0时，预测结果为1，否则为-1。

6. 更新权重

权重的更新公式： weights = weights + learning_rate * y[i] * X[i]
其中 ：

• weights 表示当前的权重值，

• learning_rate 表示学习率，即每次更新的步长，

• y[i] 表示第 i 个样本的真实标签，

• X[i] 表示第 i 个样本的特征向量。

• 当预测值和真实标签一致时，误差为0，权重值也就不需要进行更新。

• 当预测值和真实标签不一致时，误差项的符号与 y[i] 相同，误差越大，更新的幅度就越大，这样就能使感知机的预测结果更加接近真实标签。

7. 更新偏置

bias 是单层感知机的一个重要参数，它对应着感知机的阈值。偏置值的调整方式是使用随机梯度下降法，根据误差进行权重和偏置的更新。

偏置的更新公式是： bias = bias + learning_rate * y[i]

• learning_rate : 表示学习率，即每次更新的步长
• y[i] : 表示第 i 个样本的真实标签

更新公式中的 y[i] 对应的是误差项的符号，其作用是根据误差的方向来调整偏置值。
当预测值和真实标签一致时，误差为0，偏置值也就不需要进行更新。

权重的更新公式和偏置的更新公式非常类似。

这里更新权重和偏置使用的公式，也有地方会表达为：

# error 是误差
error = y - y_pred
weights = weights + learning_rate * error * X
bias = bias + learning_rate * error

和前面的公式本质是一样的，都是通过调整权重来使模型的预测更准确。

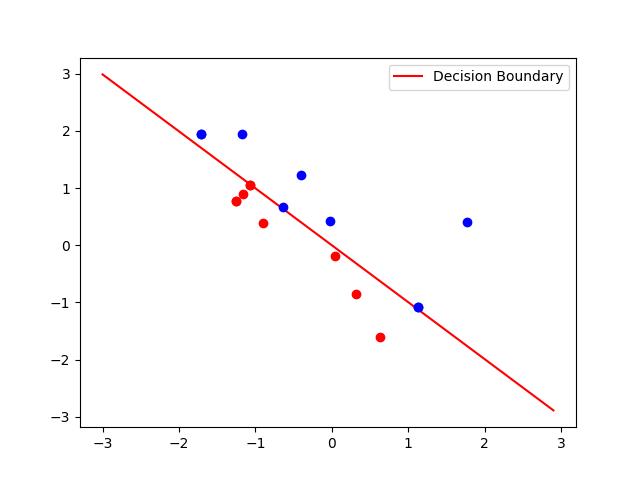
8. 绘制决策边界

决策边界就是把训练结果用函数表达出来 。
根据感知机的分类公式：

w1 * x1 + w2 * x2 + b = 0
# 得到：
x2 = (-w1 * x1 - b) / w2

这里计算的x2指的纵坐标，这样针对x1每个点计算决策值，通过plt.plot绘制结果。

# x1是从-3到3，步长为0.1
x1 = np.arange(-3, 3, 0.1)
x2 = (-weights[0] * x1 - bias) / weights[1]
plt.plot(x1, x2, 'r', label='Decision Boundary')

四、Python完整实现

import numpy as np
import matplotlib.pyplot as plt

def perceptron(X, y, lr=0.1, n_iter=100):
    # 获取样本数量和特征数量
    n_samples, n_features = X.shape

    # 初始化权重和偏置为0
    weights = np.zeros(n_features)
    bias = 0.0

    # 记录误分类点以及迭代次数
    mis_points = []
    for _ in range(n_iter):
        # 标记是否有误分类点
        mis_flag = False

        for i in range(n_samples):
            # 计算预测值
            y_pred = np.dot(weights, X[i]) + bias

            # 根据预测值和真实值调整权重和偏置
            if y_pred * y[i] <= 0:
                # 根据误差进行权重和偏置的更新
                weights += lr * y[i] * X[i]
                bias += lr * y[i]

                # 标记有误分类点
                mis_flag = True
                mis_points.append((X[i, 0], X[i, 1], y[i]))

        # 如果没有误分类点，则提前结束迭代
        if not mis_flag:
            break

    # 返回训练好的权重和偏置以及误分类点
    return weights, bias, mis_points

# 生成数据集
np.random.seed(0)
X = np.random.randn(100, 2)
y = np.array([1 if x1 + x2 >= 0 else -1 for x1, x2 in X])

# 训练模型
weights, bias, mis_points = perceptron(X, y)

# 绘制决策边界和误分类点
x1 = np.arange(-3, 3, 0.1)
x2 = (-weights[0] * x1 - bias) / weights[1]
plt.plot(x1, x2, 'r', label='Decision Boundary')
for x, y, label in mis_points:
    if label == 1:
        plt.plot(x, y, 'bo')
    else:
        plt.plot(x, y, 'ro')

plt.legend()
plt.show()