禁忌搜索_连续最优化
Posted hellobigorange
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了禁忌搜索_连续最优化相关的知识,希望对你有一定的参考价值。
文章目录
参考论文:
【1】Fitting_of_tabu_search_to_optimize_functions_of_continuous_variables
【2】基于连续函数优化的禁忌搜索算法,张晓菲,张火明
【3】一种改进的禁忌搜索算法及其在连续全局优化中的应用,郭崇慧, 岳晓晖
参考博客:TS求解二次函数的最优值
一、引言
禁忌搜索算法多用于离散变量的组合优化,如路径规划、生产调度等。但禁忌搜索也是可以用在连续变量的寻优的,其主要难点在于领域选择方式(TSP问题中是随机交换两个城市,构成候选解),第二个则在于禁忌表的生成。
二、领域选择方式
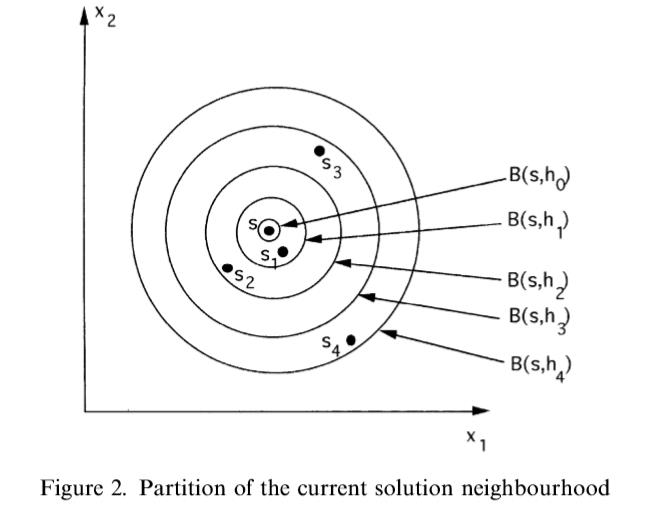
设置一个初始解s(s是多维向量,下一次的中心为下一个放入禁忌表的点),以s为中心画个大“球”,半径为r,下一个候选解就从这个“球”内取。
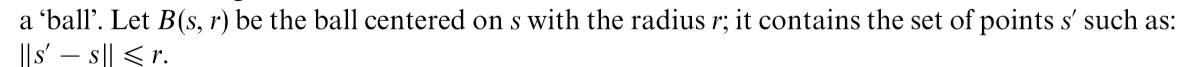
从球内取解的方式
- (1)完全随机生成解:由于候选集合长度不会太长(一般4——20),因此完全随机生成解,会使集合的解不够均匀,这样搜索到最优解的耗时较长。
- (2)分散寻找解:对"球"分区,若候选集合长度为4,将球分为4个区,第i个候选解都从第i个区中取(满足下式),这样可以保证每次迭代候选集合的解相对均匀。

半径 h i h_i hi需要根据分区方式不同,有不同的方式,如:-
(1)几何分区
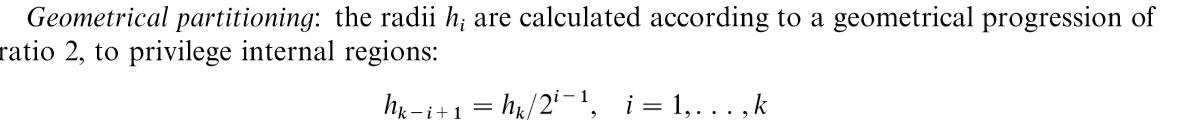
-
(2)线性分区
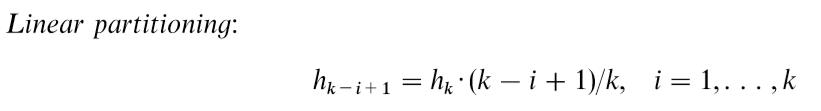
-
(3)等容分区
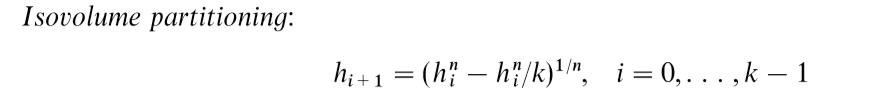
-
注意:梯度求解:可以根据梯度,每次求下降梯度对应的解的位置(候选解可以按上一轮最优解的梯度方向,按不同步长得到多个候选解,将适应度最高的且不在tabo_list的解放到tabo_list中),但是现实中的问题往往不可导,所以梯度算法有一定局限性。这里不做讲解。
若有约束,如一个分量x_l<x_i<x_u,则可以考虑:
三、禁忌表
对于连续变量不在禁忌单独的解或者目标函数值(数量太多了,禁忌它们无意义,总能找到不同的点,很难找到最优值),因此有以下两种方式:
-
(1)禁忌目标函数及目标函数 δ \\delta δ邻域
具体操作为:若禁忌表里已有目标函数值f(x),候选解 x ′ x' x′的目标函数值为f(x’)且满足 ∣ f ( x ) − f ( x ′ ) ∣ < = δ |f(x)-f(x')|<=\\delta ∣f(x)−f(x′)∣<=δ,则禁忌f(x’),反之,则将f(x’)放入禁忌表 -
(2)禁忌解及解的 δ \\delta δ邻域
具体为若禁忌表中已有解x,候选解x’,判断若 ∣ ∣ x − x ′ ∣ ∣ < = δ ||x-x'||<=\\delta ∣∣x−x′∣∣<=δ(及候选解在之前的解的邻域内),则x’已经被禁忌,判断下一个点是否被禁忌。

四、流程图
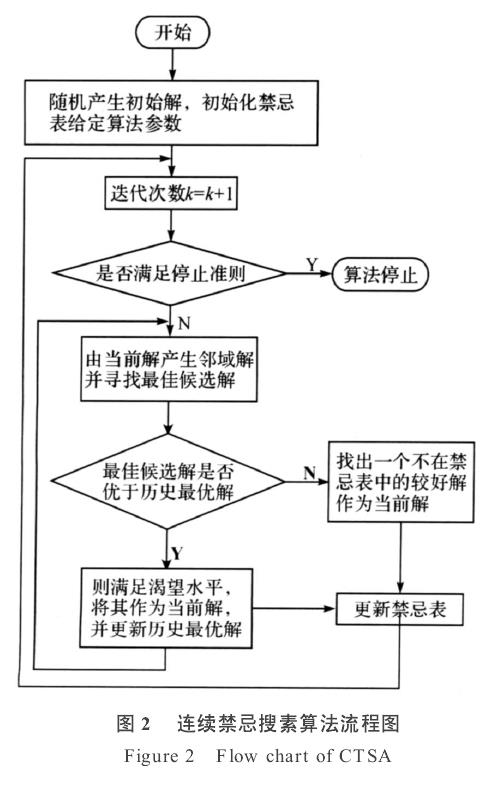
五、示例
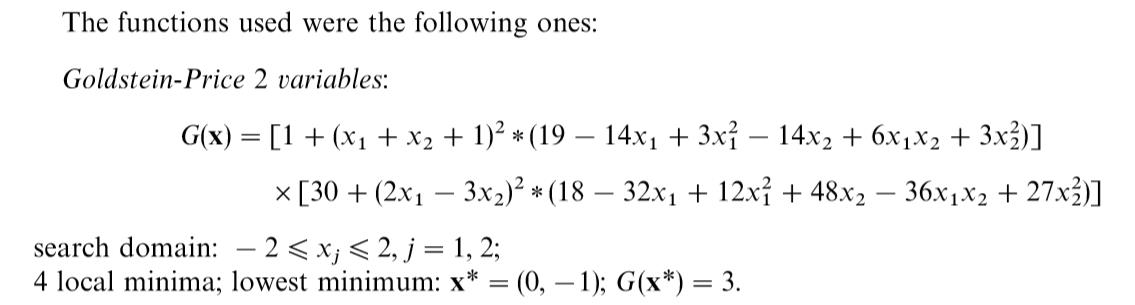
根据“球”分区的思路,我们算法的未知数有
h
k
,
h
0
h_k,h_0
hk,h0,候选集合长度k,禁忌表长度m
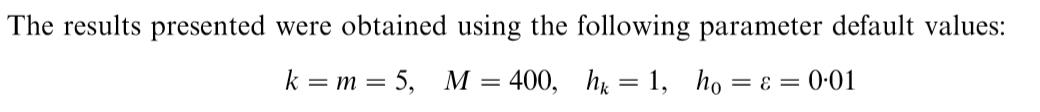
以上是关于禁忌搜索_连续最优化的主要内容,如果未能解决你的问题,请参考以下文章