论文笔记：HKMF-T: Recover From Blackouts in TaggedTime Series With Hankel Matrix Factorization

Posted 2022-03-03 UQI-LIUWJ

论文笔记：Hankel Matrix Factorization for Tagged Time Series to Recover Missing Values during Blackouts_UQI-LIUWJ的博客-CSDN博客

的后续，故而大致部分和那篇类似，本文只设计/补充一些本论文的部分，可结合上篇一起观看

TKDE 2021

0 前言

        这篇论文是之前在 ICDE’19 上发表的工作 的扩展。 这与以前的工作之间的主要区别包括：1）我们方程化了约束和假设；

2）我们解决了将 HKMF-T 应用于高维数据的问题

3）通过对数据集进行下采样，在不显着影响其有效性的情况下提高了算法的效率；

4）对参数对系统性能的影响进行了基准测试

1 trend & tagged information

        如果我们用10天的滑动平均 ，可以看到MA(10)提供了一个很是平滑的trend。

        与此同时，我们也可以发现，这里的tag信息（天气情况），对自行车结果有着很深的影响：晴天和下雪天，自行车的数量分别比之前多&比之前少

        ——>实际的时间序列通常由一个内部的光滑trend，以及外部环境的影响组成

        用符号表示，比如我们时间序列为，标签序列为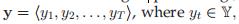

        于是我们有 x=s+e，其中s和e分别表示光滑趋势，以及外部影响部分

2 损失函数正则项

2.1 时间正则项

在论文笔记：Hankel Matrix Factorization for Tagged Time Series to Recover Missing Values during Blackouts_UQI-LIUWJ的博客-CSDN博客

 中，我们知道正则项是

 我们可以用另一种形式表示

 其中L1为

的结果就是

2.2 tag正则项

这个在上篇论文中说的不多，这里则更详细

 

我们希望同一个标签下各个时刻的e值，和这个标签的e值的平均值差距不要太大.同一个标签下的e值之差为：

 

这里I是单位矩阵

表示了某一时刻属于哪些tag的指示矩阵 ()

 是一个对角矩阵，其中，Cm是第m个tag的数量

 

 

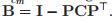
 3 传统MF在blackouts 问题中的局限性

         在blackouts问题中，时刻t的所有点的数据全部丢失，在这种情况下，时刻t的时间特征向量无法通过最小化学习 ，因为这一列的值全没有

        此外，包括 TRMF 在内的传统基于 MF 的方法不包括有关外部事件或条件如何影响序列中的值的知识，这在分析现实世界数据序列中被证明是重要的

 

4 将HKMF-T问题应用到多维数据中

原理很简单，就是叠加汉克尔矩阵

 

 5 实验部分

数据集，baseline和前作一样

评价标准相比于之间的RMSE，多了一项DTW distance

DTW 笔记： Dynamic Time Warping 动态时间规整 （&DTW的python实现）_UQI-LIUWJ的博客-CSDN博客

 同时多了一些实验（单变量时间序列），

比如正则项参数的影响：

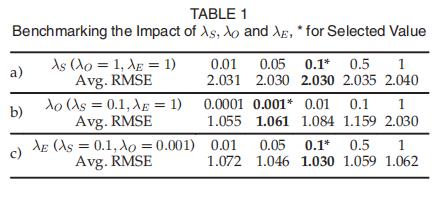
 p值的影响（p——汉克尔矩阵的列维度）

 trend 矩阵R的维度 （结论是几乎没有影响）

 

 5.1 多维时间序列的实验

        在本节中，我们展示了使用 MVCD 数据集将 HKMF-T 应用于高维数据序列的有效性。 我们将 62 个县分为 10 个区域 ，以生成 10 维数据序列，每个区域的天气状况作为我们评估的标签序列。 选择这个数据集是因为它自然地将数据分成空间连接的区域，每个区域对应一个维度

5.1.1 和baseline的比较

        在这个实验中，我们将所提出的方法的性能与 DynaMMo 进行比较，因为后者也能够捕获空间相关性和处理blackouts。

        此外，我们通过在两种设置下进行实验，比较了 HKMF-T 和 DynaMMo 在捕获不同维度之间的空间相关性方面的能力：

1）具有相关性：算法以整个 10 维数据和标签序列作为输入；

2）无相关性：算法每次执行一维。

比较是在blackouts持续时间为 的情况下进行的，以评估算法的性能。 总体结果总结在表 2 中，详细讨论如下。

 

        捕获空间相关性。从表2可以看出，两种算法都能有效地捕捉到不同维度之间的空间相关性，因为带有空间相关性的HKMF-T和DynaMMo的性能都超过了没有考虑空间相关性的对应算法。

        HKMF-T与DynaMMo相比。通过比较HKMF-T和DynaMMo在空间相关性方面的表现，可以看出，当停电时间较短时，即lb=4时，DynaMMo有一定的优势。然而，随着停电规模的扩大，HKMF-T开始显示出它的优势。