论文笔记：Mystique: Efficient Conversions for Zero-Knowledge Proofs with Applications to Machine Learnin

Posted 2023-03-12 计划是动力

论文笔记：Mystique: Efficient Conversions for Zero-Knowledge Proofs with Applications to Machine Learning

• 论文介绍
• ZK在人工智能上的应用讨论
• 现在仍然存在的问题
• ZK对于人工智能应用场景的适配和优化工作
• • 适配工作
  • 优化
  • • 前置知识：sVOLE和位乘法电路
    • ML应用程序的优化
• 论文结论

论文介绍

Mystique: Efficient Conversions for Zero-Knowledge Proofs with Applications to Machine Learning是UseNix信息安全顶会2021的论文
这篇论文目的是探索ZK算法在Machine Learning的应用和一系列优化工作

ZK在人工智能上的应用讨论

零知识（ZK）证明允许秘密证人的一方在不透露任何额外信息的情况下证明该证人的某些陈述。那么零知识证明可以适用于以下人工智能场景：

• 使用ZK协议，发现模型中的错误（例如，逃避攻击）的白帽黑客可以在零知识中证明该错误的存在，例如，他们可以证明M（x1）≠ M（x2）的两个closed输入x1和x2的知识。
• 使用ZK协议，模型所有者可以公开提交一个模型，然后在零知识的情况下证明提交的模型应用于用户提交的输入，从而产生所要求的结果。
• ML模型可以在私有测试数据上进行评估。在这里，测试数据的所有者可以公开承诺其数据；然后，模型培训师可以将其模型（使用独立的训练数据开发）发送给数据所有者，数据所有者在本地评估模型的准确性。数据所有者可以使用ZK协议来证明提交的模型是在提交的数据上执行的。
  
  

现在仍然存在的问题

问题：最先进的zk-SNARK要求证明器的内存与语句大小成比例

ZK对于人工智能应用场景的适配和优化工作

适配工作

• 算术/布尔值。受安全计算设置中类似想法的启发，我们设计了优化的协议，以在基于sVOLE的零知识的上下文中有效地在算术值和布尔值之间进行转换（以支持混合模式电路）。

• 已提交/已验证的值。为了允许在ZK证明中使用公开提交的值，我们设计了一个有效的协议，该协议将这些值转换为由证明者和验证者私下认证的值，因此可以直接在基于sVOLE的ZK协议中使用。

• 定点/浮点值。我们为符合IEEE-754标准的浮点运算设计了电路，并设计了有效的协议。

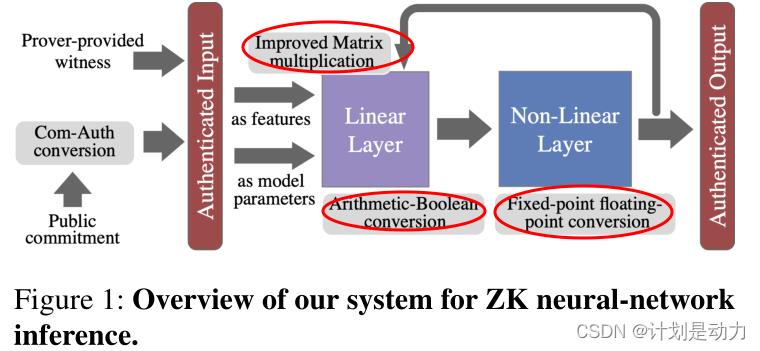
优化

除上述之外，我们还为矩阵乘法设计了一个有效的ZK证明，使得所需的私有乘法的数量在矩阵大小中是次线性的。与之前最著名的ZK矩阵乘法证明相比，我们的ZK协议将执行时间提高了7倍。

前置知识：sVOLE和位乘法电路

M是引入 $\delta$ 后的一个模糊值

论文里的$F_q$素域满足以下性质：
$$\begin{gathered} F_p满足： \\ GF(p)中所有非零元素都存在逆元 \\ GF(p)内所有的运算都是模p实现的 \end{gathered}$$

例如对于：
$$\begin{gathered} 素域GF(5)=0,1,2,3,4,即模5 \\ 那可以得到a=2的加法逆元-a为3(2+(3)mod5=0) \\ a=2的乘法逆元a^{-1}为3,(2\times (3)mod5=1) \end{gathered}$$

论文里的${F_{q^k}}^n$扩域($F_{q^k}$上的n维向量空间)，参数就是均匀的随机n个值

sVOLE位电路乘法门：证明z = x * y (x,y,z是[x],[y],[z]其中的一位，可以认为是索引为i的乘法门电路）
双方可以通过随机线性组合一次检查上述所有N个方程：

现在把sVOLE作为一个黑盒，考虑怎么把它用在人工智能的矩阵运算中呢？

ML应用程序的优化

这里的思想就是把$n\times m$维度的证明优化成向量程度的证明：

$$\begin{gathered} [A]\cdot [B]=[C] \\ \Rightarrow u^T\cdot [A]\cdot [B]\cdot v=u^T\cdot [C]\cdot v \end{gathered}$$
左乘一个均匀随机分布的向量$u\in (F_{q^k}{)}^n$,右乘均匀随机向量$v\in (F_{q^k}{)}^l)$
$$\Rightarrow (u^T\cdot [A])\cdot ([B]\cdot v)=u^T\cdot [C]\cdot v$$
令$[x{]}^T=[u^T\cdot A]\in (F_{q^k}{)}^m,[y]=[B\cdot v]\in (F_{q^k}{)}^m,[z]=[u^T\cdot C\cdot v]\in F_{q^k}$
$$\Rightarrow [x{]}^T\cdot [y]=[z]$$
经历过以上转换后就转化成了sVOLE的位验证电路,我们只需要采样一些随机向量u和v就可以完成验证，与之前最著名的ZK矩阵乘法证明相比，该论文的ZK协议将执行时间提高了7倍。

论文结论

ResNet-101推理的执行时间分解。顶栏用于公共模型私有特征推断；底部的条用于私有模型私有特征推断。网络带宽被限制为200 Mbps。

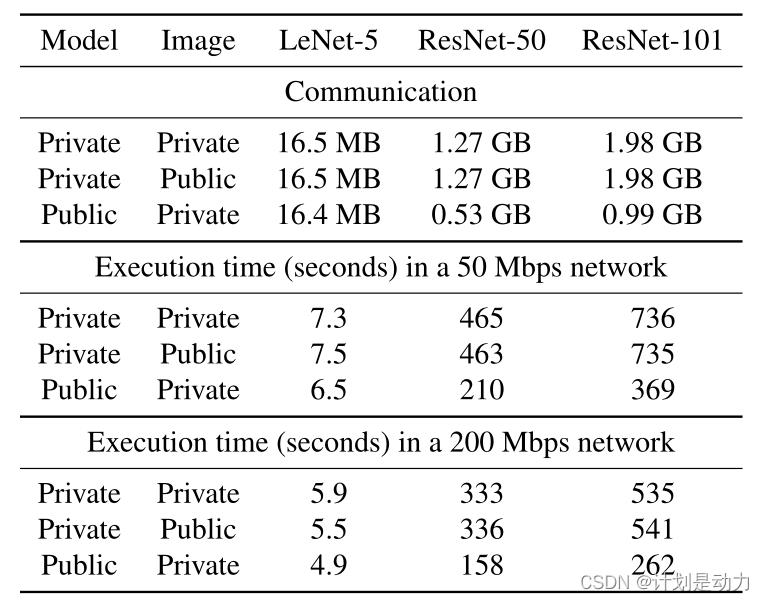
零知识神经网络推理的性能。所有模型都使用CIFAR-10数据集进行训练。