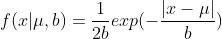机器学习笔记：正则化

Posted 2023-03-12 UQI-LIUWJ

1 Lp范数

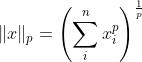
1.1 L0范数

• 表示向量中非零元素的个数
  • 
• 通过最小化 L0 范数，来寻找最少最优的稀疏特征项
• 但是L0范数的最优化问题是一个NP 难问题，同时L0范数是非凸的
  • ——>实际应用中需要对L0范数进行凸松弛
• 从理论上来说，L1范数是L0范数的最优凸近似
  • ——>常用L1范数来代替L0范数，以进行优化

1.2 L1范数

• 
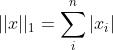
• L1 范数就是向量各元素的绝对值之和
• L1范数也被称为是"稀疏规则算子"（Lasso regularization）

1.3 L2范数

机器学习笔记：岭回归（L2正则化）_岭回归 正则化_UQI-LIUWJ的博客-CSDN博客

• 以 L2 范数作为正则项可以得到稠密解，即每个特征对应的参数 𝑤 都很小，接近于 0 但是不为 0
• 此外，L2 范数作为正则化项，可以防止模型为了迎合训练集而过于复杂造成过拟合的情况，从而提高模型的泛化能力。

1.3.1 L1范数和L2范数的区别（解范围的角度）

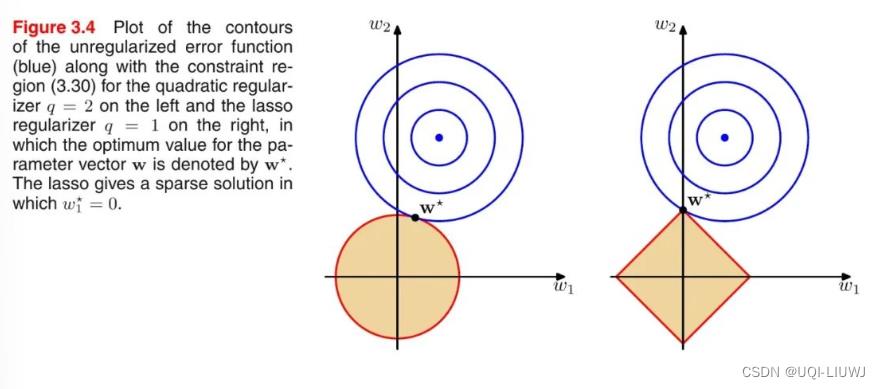
•  蓝色的圆圈表示问题可能的解范围，橘色的表示正则项可能的解范围
•  整个目标函数（原问题+正则项）有解当且仅当两个解范围相切
  • 由于 L2 范数解范围是圆，所以相切的点有很大可能不在坐标轴上
    • ——>稠密解
  • 由于 L1 范数是菱形（顶点是凸出来的），其相切的点更可能在坐标轴上
    • ——>稀疏解

1.3.2 L1范数和L2范数的区别（贝叶斯先验的角度）

• 从贝叶斯先验的角度看，当训练一个模型时，仅依靠当前的训练数据集是不够的，为了实现更好的泛化能力，往往需要加入先验项，而加入正则项相当于加入了一种先验。
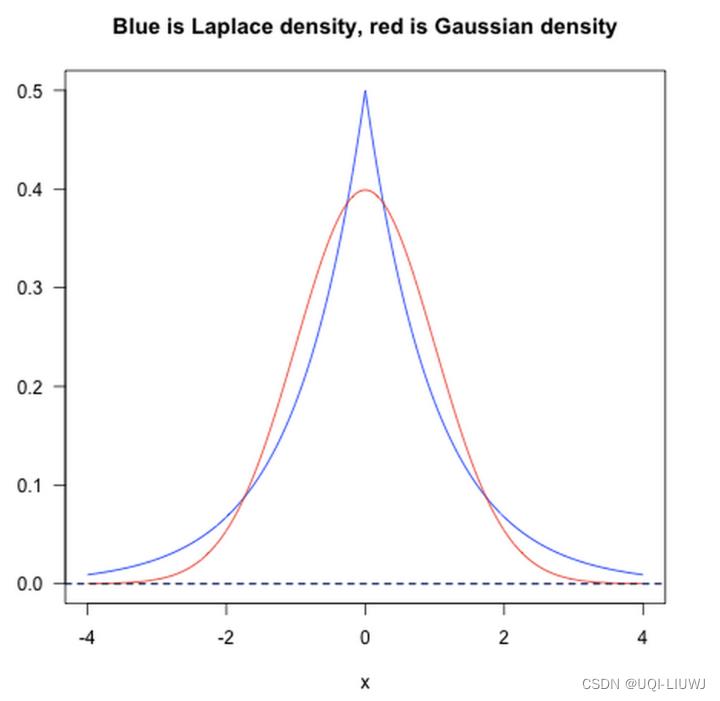
  • L1 范数相当于加入了一个 Laplacean 先验
    • 
  • L2 范数相当于加入了一个 Gaussian 先验。
    • 
• 

 2 Dropout

• 在 DNNs 训练的过程中以概率 𝑝 丢弃部分神经元，即使得被丢弃的神经元输出为 0
  •  

2.1 Dropout 正则化效果理解

• 在 Dropout 每一轮训练过程中随机丢失神经元的操作相当于多个 DNNs 进行取平均，因此用于预测时具有 vote 的效果。（伪*集成学习）
• 减少神经元之间复杂的共适应性。
  • 当隐藏层神经元被随机删除之后，使得全连接网络具有了一定的稀疏化，从而有效地减轻了不同特征的协同效应。
  • 也就是说，有些特征可能会依赖于固定关系的隐含节点的共同作用，而通过 Dropout 的话，就有效地阻止了某些特征在其他特征存在下才有效果的情况，增加了神经网络的鲁棒性。