数字信号处理线性时不变系统 LTI ( 判断某个系统是否是 “ 非时变 “ 系统 | 案例三 )
Posted 韩曙亮
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数字信号处理线性时不变系统 LTI ( 判断某个系统是否是 “ 非时变 “ 系统 | 案例三 )相关的知识，希望对你有一定的参考价值。
文章目录
一、判断系统是否 " 非时变 "
1、案例二
给定 输入序列 x ( n ) = 0 , 1 , 2 , 3 , 4 , 5 , 0 x(n) = \\ 0, 1 , 2, 3, 4, 5 , 0 \\ x(n)=0,1,2,3,4,5,0 , n n n 取值 − 1 -1 −1 ~ 5 5 5
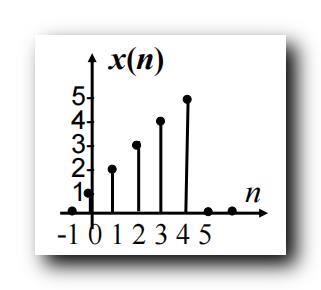
判断其输出序列 y ( n ) = x ( n 2 ) y(n) = x(n^2) y(n)=x(n2) 的 " 变换 " 操作是否是 " 时不变 " 的 ;
y ( n ) = x ( n 2 ) y(n) = x(n^2) y(n)=x(n2) 变换操作 :
y ( n ) y(n) y(n) 只有在 n = − 1 , 0 , 1 , 2 n = -1 , 0 , 1 , 2 n=−1,0,1,2 取值时 , 才有值 ,
如果
n
=
3
n = 3
n=3 ,
n
2
=
9
n^2 = 9
n2=9 ,
x
(
9
)
x(9)
x(9) 没有值 ;
如果
n
=
4
n = 4
n=4 ,
n
2
=
16
n^2 = 16
n2=16 ,
x
(
16
)
x(16)
x(16) 没有值 ;
如果
n
=
5
n = 5
n=5 ,
n
2
=
25
n^2 = 25
n2=25 ,
x
(
10
)
x(10)
x(10) 没有值 ;
因此 , 正常变换后 , y ( n ) y(n) y(n) 的取值是 n = 0 , 1 , 2 n = 0 , 1 , 2 n=0,1,2 时的取值 ,
当
n
=
−
1
n = -1
n=−1 时 ,
y
(
n
)
=
x
(
n
2
)
=
x
(
(
−
1
)
2
)
=
x
(
1
)
=
2
y(n) = x(n^2) = x((-1)^2) = x(1) = 2
y(n)=x(n2)=x((−1)2)=x(1)=2 ;
当
n
=
0
n = 0
n=0 时 ,
y
(
n
)
=
x
(
n
2
)
=
x
(
0
2
)
=
x
(
0
)
=
1
y(n) = x(n^2) = x(0^2) = x(0) = 1
y(n)=x(n2)=x(02)=x(0)=1 ;
当
n
=
1
n = 1
n=1 时 ,
y
(
n
)
=
x
(
n
2
)
=
x
(
1
2
)
=
x
(
1
)
=
2
y(n) = x(n^2) = x(1^2) = x(1) = 2
y(n)=x(n2)=x(12)=x(1)=2 ;
当
n
=
2
n = 2
n=2 时 ,
y
(
n
)
=
x
(
n
2
)
=
x
(
2
2
)
=
x
(
4
)
=
5
y(n) = x(n^2) = x(2^2) = x(4) = 5
y(n)=x(n2)=x(22)=x(4)=5 ;
其中 − 1 -1 −1 和 1 1 1 的平方都为 1 1 1 , 合并成一个 ;
x ( n ) x(n) x(n) 正常变换后的取值为 :
y ( n ) = 1 , 2 , 5 y(n) = \\ 1, 2, 5 \\ y(n)=1,2,5
① 时不变系统概念
时不变系统 ( time-invariant ) : 系统特性 , 不随着时间的变化而变化 ;
y ( n − m ) = T [ x ( n − m ) ] y(n - m) = T[x(n-m)] y(n−m)=T[x(n−m)]
输入延迟后 , 输出也随之延迟 ;
与 " 时不变 " 系统对应的是 " 时变 " 系统 ;
② 先变换后移位
将 " 输出序列 " 进行移位 , 先 " 变换 " 后 " 移位 " ;
先将 " 输入序列 " 进行 " 变换 " 操作 , 得到 " 输出序列 " , 然后对 输出序列 进行 " 移位 " 操作 ;
其中 " 变换 " 指的是 , 离散时间系统 , 将 " 输入序列 " 变换 为 " 输出序列 " , 输入序列 到 输出序列 之间的操作 , 是 " 变换 " ;
变换操作 : 先将 输入序列 x ( n ) x(n) x(n) 进行 变换 操作 , 得到 输出序列 x ( n 2 ) x(n^2) x(n2) ,
移位操作 : 然后 对 x ( n 2 ) x(n^2) x(n2) 输出序列 进行移位 n − n 0 n - n_0 n−n0 得到 x ( ( n − n 0 ) 2 ) x((n-n_0)^2) x((n−n0)2) ,
完整运算过程如下 :
y ( n − n 0 ) = x ( ( n − n 0 ) 2 ) y(n - n_0) = x((n-n_0)^2) y(n−n0)=x((n−n0)2)
先变换 , 变换后输出为 :
y
(
n
)
=
1
,
2
,
5
y(n) = \\ 1, 2, 5 \\
y(n)=1,2,5
后移位的取值为 : 向右移一位 ;
y ( n − 1 ) = 0 , 1 , 2 , 5 y(n-1) = \\ 0, 1, 2, 5 \\ y(n−1)=0,1,2,5
③ 先移位后变换
将 " 输入序列 " 进行移位 , 先进行移位 , 将 " 输入序列 x ( n ) x(n) x(n) " 先进行 " 移位 " 操作 , 得到 新的 " 输入序列 " 为 x ( n − n 0 ) x(n-n_0) x(n−n0) , 然后 对新的输入序列进行 " 变换 " 操作 , 得到 " 输出序列 " ;
变换过程是 T [ x ( n − n 0 ) ] = x ( n 2 − n 0 ) T[x(n - n_0)] = x(n^2 - n_0) T[x(n−n0)]=x(n2−n0) , 变换时 , 只是将 n n n 值变为 n 2 n^2 n2 , n 0 n_0 n0 值不动 ;
x ( n − n 0 ) x(n-n_0) x(n−n0) 变换时 , 只将 n n n 乘以 数字信号处理线性时不变系统 LTI ( 判断某个系统是否是 “ 非时变 “ 系统 | 案例二 )
数字信号处理线性时不变系统 LTI ( 判断某个系统是否是 “ 非时变 “ 系统 | 案例一 | 先变换后移位 | 先移位后变换 )
数字信号处理线性时不变系统 LTI “ 输入 “ 与 “ 输出 “ 之间的关系 ( LTI 系统单位脉冲响应 | 卷积 | 卷积推导过程 )
数字信号处理线性时不变系统 LTI “ 输入 “ 与 “ 输出 “ 之间的关系 ( 线性卷积起点定理推导过程 )
数字信号处理离散时间系统 ( 离散时间系统概念 | 线性时不变系统 LTI - Linear time-invariant )