半瓶子晃荡

Posted 2022-02-25 卓晴

 

  在面包板社区 中的一篇博文： 号称能“炸出各种半瓶子晃荡的人"的电路题 介绍了一个电路问题：

一个额定电压为交流220V/50Hz、额定功率为100W的白炽灯与一个整流二极管串联，再连接至220V交流市电，如果忽略二极管的压降以及灯丝随温度改变而发生的变化，则白炽灯的实际功率是多少？

A：100W  B: 50W  C: 25W  D: 22.5W。

▲ 图1.1 半波整流电压信号的功率输出

  根据题目中的假设，正确的答案应该是 B：50W 。

  文章分析，据说这道题目很多 “对于电路理解半瓶子晃荡” 的人会选择 C：25W ，或者 D:22.5W 。

  选择 C 的人会认为，既然电压波形少了一半，那就是电压 $U$ 小了一半。根据功率： $P=U^2/R$ ，那么电灯上的功率自然就只剩下原来的四分之一，也就是25W。

  选择 D 的人会认为，半波（正弦波 0 ~ π）的平均值为峰值 $U_P$ 的 $2/\pi$ ，而正弦波的有效值 $U_{RMS}$ 为峰值的 $\sqrt{2}/\pi$ ，那么半波的有效值应该在原有效值一半的基础上，乘以 $\sqrt{2}/\pi$ ，也就是 $0.5\times \sqrt{2}/\pi =22.5\%$ 。

 

  如果是从物理概念上来求解这个问题，则从电压信号的功率定义上理解。功率反映了电压信号在负载上的做功速率。这里的做功就是输出的电能。速率表示单位时间内的做功多少。

  对于属于周期信号的交流电，它的功率 $P$ 可以由一个周期内输出电能 $E_T$ 除以周期时间 $T$ 获得：$$P=\frac{E_T}{T}$$

  根据本题给出的条件，理想二极管整流后的半波正弦波在理想灯泡（等价为恒定电阻）输出功率，由于在同样周期内输出电能减少了一半（根据正弦波的对称性）所以功率也减少为原来的一半，即50W。

▲ 图1.2.1 周期信号的功率可以由一个周期内的信号能量除以信号周期获得

  一个正弦电压信号可以由其三要素来决定：幅值 $U_P$ 、频率 $f_0$ 和相位 $\theta$ 。其中幅值决定了电压输出功率。如果负载是电阻，我们把能够产生相同功率的直流电压所对应的数值 $U_{RMS}$ 为交流信号的有效值，经过简单数学推导可以知道：$$U_{RMS}=\frac{1}{\sqrt{2}}{U}_P$$

  对于峰值为 $U_P$ 的半波交流信号所对应的有效值，根据前面分析应该是： $U_{RMS}=0.5U_P$ 。

 

  一个好的提问，往往会引起更多的联想。比如以下两个问题。

节能灯对应的答案是多少？

  实际上，现在我们常见的电灯都属于节能灯，通过电路设计往往它们可以适应的电压范围从110V ~ 250V而且保持功率不变。特别是一些带有功率因数补偿的节能灯，对于只有半波整流电压供电时，仍然可以获得稳定的功率输出。

  所以，现在对于大多数的节能灯来讲，上面问题答案应该选择： A:100W 。

真实白炽灯功率是多少？

  前面的问题中假设了电灯是理想的，也就是它的阻值不随着输出功率变化而改变。我们知道这实际上不符合实际上电灯的物理特性。

  在 测量6J1电子管的一些基本特性 测试了电子管阴极加热灯丝电阻的变化，室温时对应电阻为 5.6Ω，施加额定直流电压（6.3V）之后，对应电阻为36.7Ω。显示了灯丝随着温度增加而增加的特点。

  在 How hot does a tungsten filament get in a lightbulb? 文章中给出了普通的白炽灯泡钨丝的温度达到2500 ~ 3300 ℃左右。

▲ 图2.1.1 灯泡里面的钨丝电子显微镜图像

  在 Resistivity of tungsten as a function of temperature 中给出了不同温度下，钨灯丝电阻率的变化拟合函数。下图摘录自该文档，可以看到在很大的温度范围内，钨的电阻率与温度之间呈现线性关系。

▲ 图2.1.2 金属钨的电阻率随着温度变化拟合参数

  根据 如何测量体温 查到的黑体辐射热量与温度呈现四次方关系：

$$W_e=E\cdot \sigma \cdot T^4\cdot A$$

其中：

We：热辐射能力
E：物体辐射系数
σ：Stefan-Boltzmann常数
T：物体绝对温度
A：辐射面积

  好了，有了上面关于白炽灯泡的了解，将灯泡的电子特性作如下假设：

• 灯丝的电阻与灯丝的绝对温度呈线性关系；
• 灯丝的辐射功率等于交流电作用在灯丝电阻上的平均功率；
• 灯丝温度的四次方与辐射功率之间成线性关系；

  那么，此时正确的答案应该是多少呢？

 

  距今白炽灯泡的发明已经过去了一个多世纪，Dan Maclsaac, Gary Kanner等在 1999年12月发表了一篇文章： Basic Physics of the Incandescent Lamp(Lightbulb) ，详细介绍了白炽灯泡的物理基础。内容详实，很是吸引人。这篇文章很值得读一读。

▲ 图2.2.1 Basic Physics of the Incandescent Lamp 以及作者

▲ 图2.2.2 这个谜语的谜底： A joke

问题求解

  上面对于真实灯泡输出功率的可以通过列写方程来求解，也可以通过迭代的方式求解灯泡功率，更能凸显灯泡内部热平衡的过程。

  比如，不失一般性，可以假设正常供电下：

正常供电下：

灯丝温度T0：2500℃
输出功率P0：100W
电压有效值Urms：220V

  此时可以计算出灯丝电阻： $R_0=484\Omega$ ，以及对应黑体辐射系数 $E\cdot \sigma \cdot A$ 的数值。

  半波整流后，电压的有效值降低为为 $U_1=220/\sqrt{2}$ 。此时可以计算出对应的灯丝功率 $P_1$ ，温度 $T_1$ ，以及对应的电阻 $R_1$ 。

  再根据 $R_1$ 重新计算功率，温度，和电阻。如此迭代几次便可以获得最终的灯丝温度、电阻和功率。

  下面显示了电灯功率随着迭代次数增加变化的情况。

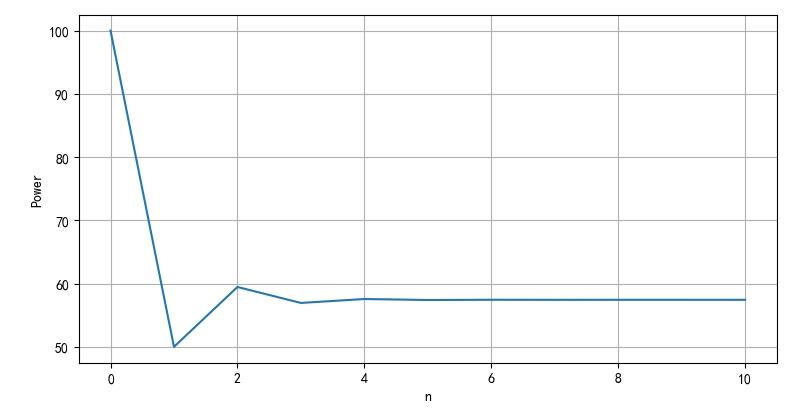
▲ 图2.5 十次迭代后的灯泡功率

  最终电灯输出功率为：$$P_1=57.4W$$。可以验证，最终的输出功率与开始假设的起始条件（ $U_0=220V,T_0=2500$ ）无关。

from headm import *

T0 = 2500
U0 = 220
P0 = 100
R0 = U0**2/P0
E0 = (P0/T0**4)

printf(R0, E0)

pdim = [P0]
tdim = [T0]
rdim = [R0]

U1 = U0/sqrt(2)

for i in range(10):
    p = U1**2/rdim[-1]
    t = (p/E0)**(1/4)
    r = t*R0/T0

    pdim.append(p)
    tdim.append(t)
    rdim.append(r)

    printff(p,t,r)

plt.plot(pdim)

plt.xlabel("n")
plt.ylabel("Power")
plt.grid(True)
plt.tight_layout()
plt.show()

求解问题

根据灯丝辐射功率等于输入电功率 $p$ 与灯丝温度 $t$ 的四次方成正比。在正弦波作用下，灯泡的功率为 $P_0=100W$ ，对应的灯丝温度为 $T_0$ 。那么有：$$\frac{p}{P_0}=(\frac{t}{T_0}$$

灯丝温度对于紫外线灯击穿的影响

收藏 | Pytorch 常用损失函数拆解

法线变换需要右乘矩阵，顶点变换需要左乘矩阵

法线变换需要右乘矩阵，顶点变换需要左乘矩阵

紫外线灯管击穿电压

紫外线灯管击穿电压