C语言每日一练 —— 第22天:零基础学习动态规划
Posted 英雄哪里出来
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了C语言每日一练 —— 第22天:零基础学习动态规划相关的知识,希望对你有一定的参考价值。
文章目录
一、前言
之前的文章中,我有讲过一些经典的动态规划,例如:最长单调子序列、最长公共子序列、最小编辑距离、背包问题、记忆化搜索、区间DP、数位DP,其中不乏一些较难的内容,不太好理解,所以这篇文章,我会对基础的动态规划再做一个梳理,从最简单的线性DP开始讲起,来谈谈零基础如何一步一步搞清楚动态规划。
点击文末【阅读原文】可跳转到视频讲解。
二、递推
首先让我们来看一下,零基础学习动态规划前必须要看的一道题。
1、斐波那契数列
1)题目描述
给定一个 n ( 0 ≤ n ≤ 30 ) n (0 \\le n \\le 30) n(0≤n≤30),求斐波那契数列的第 n n n 项。
2)算法分析
斐波那契数列就是一个从 0 0 0 和 1 1 1 开始,其后每一项都等于前两项的和,就像这样:
F ( 0 ) = 0 F ( 1 ) = 1 F ( n ) = F ( n − 1 ) + F ( n − 2 ) , 其 中 n > 1 F(0) = 0 \\\\ F(1) = 1 \\\\ F(n) = F(n - 1) + F(n - 2),其中 n > 1 F(0)=0F(1)=1F(n)=F(n−1)+F(n−2),其中n>1
拿到这个题目,我们首先来看题目范围, n n n 最多不超过 30,那是因为斐波那契数的增长速度很快,是指数级别的。所以如果 n n n 很大,就会超过 c语言 中32位整型的范围。这是一个最基础的递推题,递推公式都已经告诉你了,我们要做的就是利用一个循环来实现这个递推。
3)源码详解
int fib(int n)
int i; // (1)
int f[31] = 0, 1; // (2)
for(i = 2; i <= n; ++i) // (3)
f[i] = f[i-1] + f[i-2]; // (4)
return f[n]; // (5)
- ( 1 ) (1) (1) 首先定义一个循环变量;
- ( 2 ) (2) (2) 再定义一个数组记录斐波那契数列的第 n n n 项,并且初始化第 0 0 0 项 和 第 1 1 1 项。
- ( 3 ) (3) (3) 然后一个 for 循环,从第 2 项开始;
- ( 4 ) (4) (4) 利用递推公式逐步计算每一项的值;
- ( 5 ) (5) (5) 最后返回第 n n n 项即可。
4)简单复盘
递推其实是一种最简单的状态转移,如果对状态的概念还比较模糊,没有关系。接下来的内容,我会不断给你灌输状态的概念,接下来让我们来看另一道题,它是斐波那契数列的简单应用。
2、爬楼梯
1)题目描述
给定一个 n ( 1 ≤ n ≤ 45 ) n (1 \\le n \\le 45) n(1≤n≤45) 代表总共有 n n n 阶楼梯,一开始在第 0 0 0 阶,每次可以爬 1 1 1 或者 2 2 2 个台阶,问总共有多少种不同的方法可以爬到楼顶。
2)算法分析
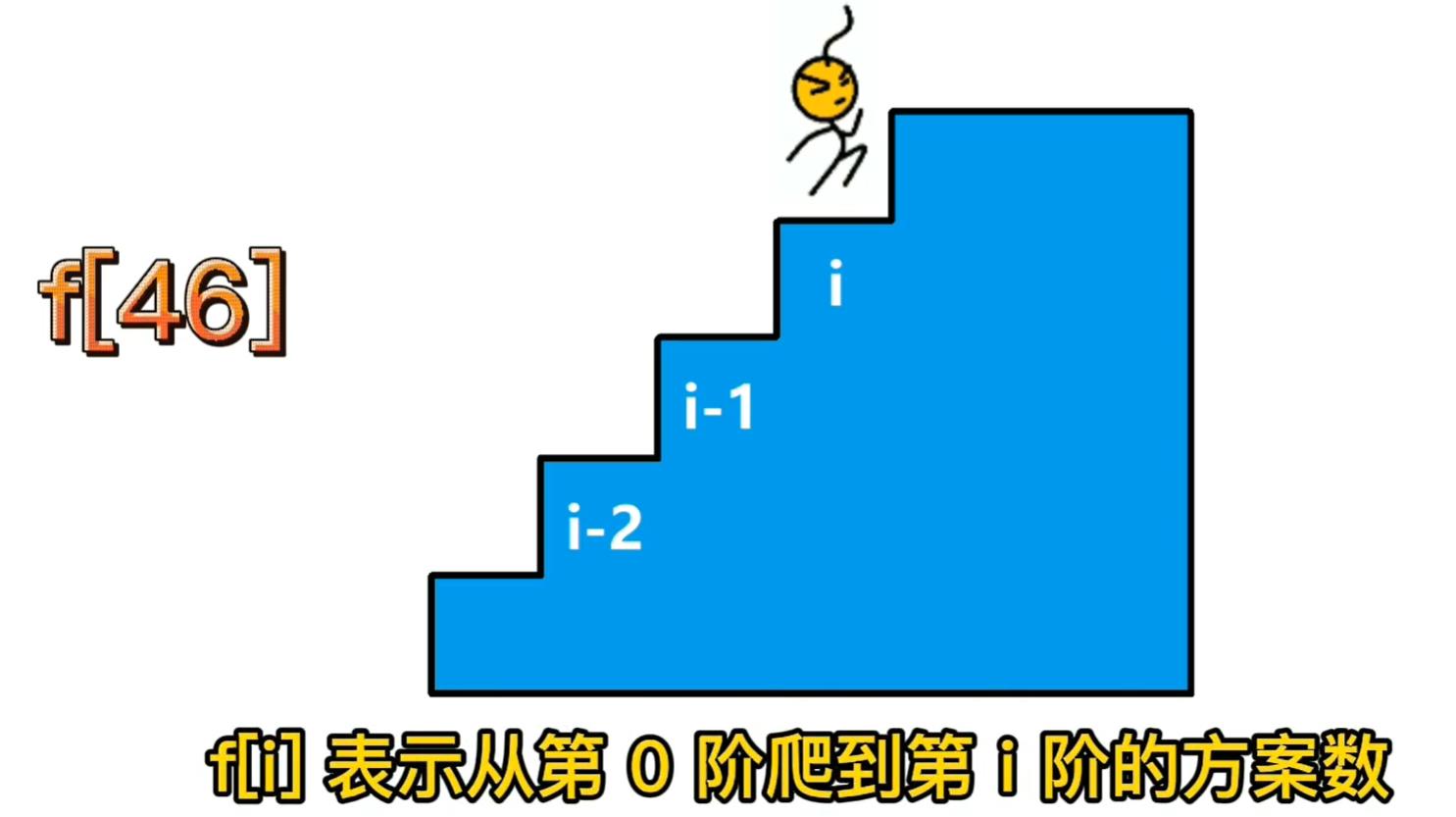
我们定义一个数组 f [ 46 ] f[46] f[46],其中 f [ i ] f[i] f[i] 表示从第 0 0 0 阶爬到第 i i i 阶的方案数。
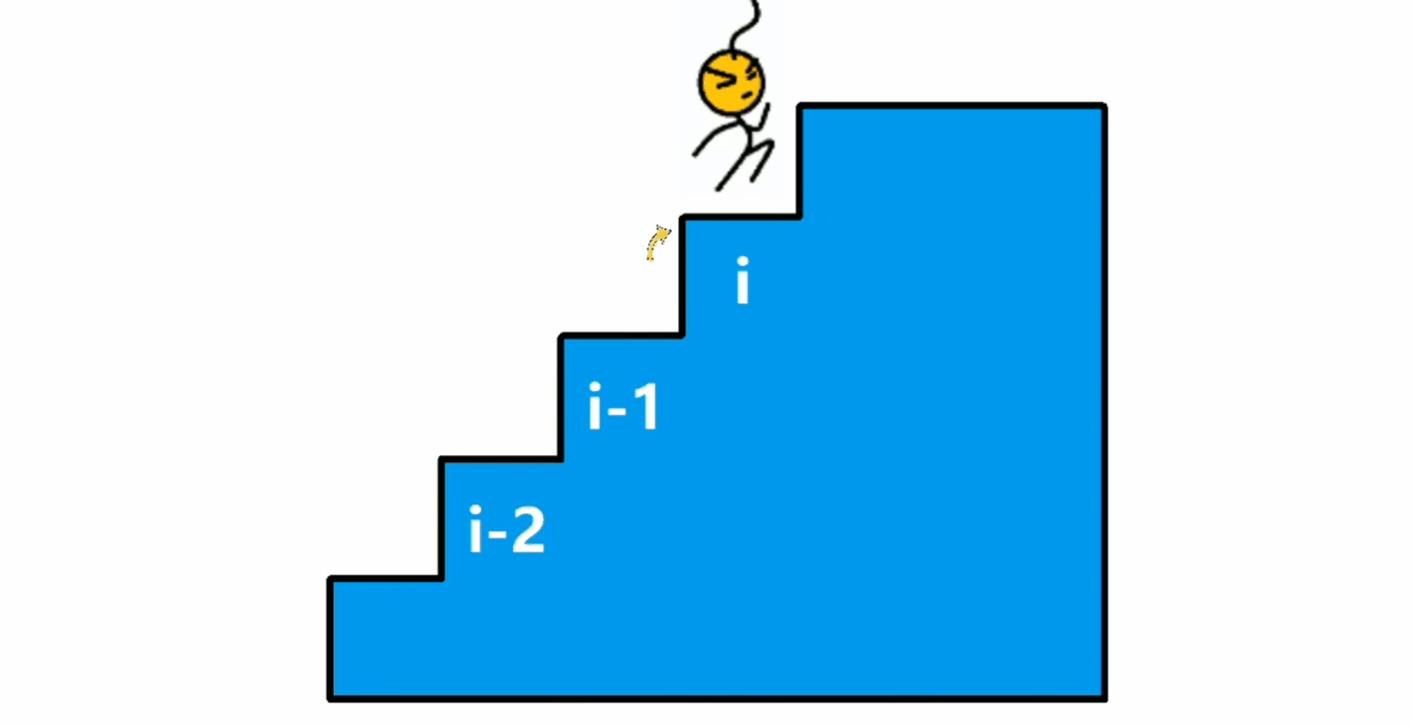
由于每次可以爬 1 1 1 或者 2 2 2 个台阶,所以对于第 i i i 阶楼梯来说,所以要么是从第 i − 1 i-1 i−1 阶爬过来的,要么是从 i − 2 i-2 i−2 阶爬过来的,如图所示:
于是得出一个递推公式
f [ i ] = f [ i − 1 ] + f [ i − 2 ] f[i] = f[i-1] + f[i-2] f[i]=f[i−1]+f[i−2]
我们发现这个就是斐波那契数列,你可以叫它递推公式,也可以叫它状态转移方程。这里的 f [ i ] f[i] f[i] 就是状态的概念,从一个状态到另一个状态就叫状态转移。
当然我们还要考虑初始状态, f [ 0 ] f[0] f[0] 代表从第 0 0 0 阶到第 0 0 0 阶的方案数,当然就是 1 1 1 啦, f [ 1 ] f[1] f[1] 代表从第 0 0 0 阶到第 1 1 1 阶的方案数,由于只能走 1 1 1 阶,所以方案数也是 1 1 1。
3)源码详解
int climbStairs(int n)
int i; // (1)
int f[46] = 1, 1; // (2)
for(i = 2; i <= n; ++i) // (3)
f[i] = f[i-1] + f[i-2]; // (4)
return f[n]; // (5)
- ( 1 ) (1) (1) 首先定义一个循环变量;
- ( 2 ) (2) (2) 再定义一个数组 f [ i ] f[i] f[i] 代表从第 0 0 0 阶爬到第 i i i 阶的方案数;
- ( 3 ) (3) (3) 然后一个 for 循环,从第 2 项开始;
- ( 4 ) (4) (4) 利用递推公式逐步计算每一项的值;
- ( 5 ) (5) (5) 最后返回第 n n n 项即可。
4)简单复盘
通过这道题我们发现,一个问题可以有不同的问法,但是最后解法是相同的。如何把复杂的问题转换成我们学过的内容就是抽象问题的能力,抽象这个词很抽象,需要不断的练习才能领悟其中的精髓。
三、线性DP
递推也是某种意义上的线性DP,线性DP的最大特征就是状态是用一个一维数组表示的,一般状态转移的时间复杂度为
O
(
1
)
O(1)
O(1) 或者
O
(
n
)
O(n)
O(n)。
让我们来看一个线性DP的经典例子来加深理解。
1、使用最小花费爬楼梯
1)题目描述
给定一个 n ( n ≤ 1000 ) n(n \\le 1000) n(n≤1000),再给定一个 n n n 个整数的数组 c o s t cost cost, 其中 c o s t [ i ] cost[i] cost[i] 是从楼梯第 i i i 个台阶向上爬需要支付的费用。一旦支付此费用,即可选择向上爬一个或者两个台阶。
可以选择从下标为 0 0 0 或下标为 1 1 1 的台阶开始爬楼梯,请计算并返回达到楼梯顶部的最低花费。
2)算法分析
我们发现这题和之前的爬楼梯很像,只不过从原来的计算方案数变成了计算最小花费。
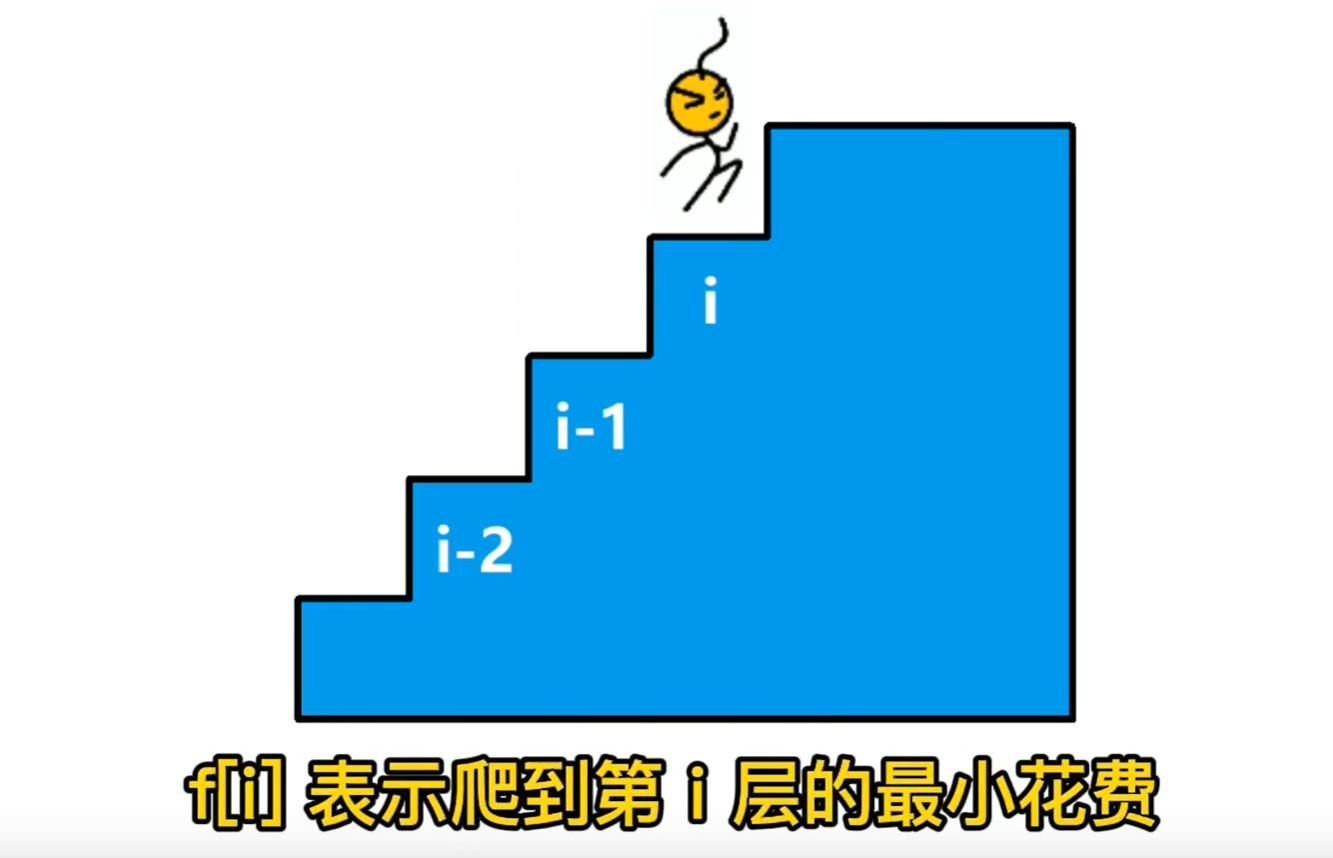
我们尝试用一个数组来表示状态: f [ i ] f[i] f[i] 表示爬到第 i i i 层的最小花费。
由于每次只能爬 1 1 1 个或者 2 2 2 个台阶,所以 f [ i ] f[i] f[i] 这个状态只能从 f [ i − 1 ] f[i-1] f[i−1] 或者 f [ i − 2 ] f[i-2] f[i−2] 转移过来:
1)如果从 i − 1 i-1 i−1 爬上来,需要的花费就是 f [ i − 1 ] + c o s t [ i − 1 ] f[i-1] + cost[i-1] f[i−1]+cost[i−1];
2)如果从 i − 2 i-2 i−2 爬上来,需要的花费就是 f [ i − 2 ] + c o s t [ i − 2 ] f[i-2] + cost[i-2] f[i−2]+cost[i−2];
没有其他情况了,而我们要 求的是最小花费,所以 f [ i ] f[i] f[i] 就应该是这两者的小者,得出状态转移方程:
f [ i ] = m i n ( f [ i − 1 ] + c o s t [ i − 1 ] , f [ i − 2 ] + c o s t [ i − 2 ] ) f[i] = min(f[i-1] + cost[i-1], f[i-2] + cost[i-2]) f[i]=min(f[i−1]+cost[i−1],f[i−2]+cost[i−2])
然后考虑一下初始情况 f [ 0 ] f[0] f[0] 和 f [ 1 ] f[1] f